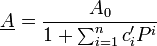- Besselfilter
-
Ein Bessel-Filter ist ein Frequenzfilter, bei dessen Entwurf folgende (äquivalente) Eigenschaften angestrebt wurden:
- optimales „Rechteckübertragungsverhalten“, d. h. eine Wellenform, deren Frequenzanteile innerhalb des Durchlassbereichs des Filters liegen, erscheint (bis auf eine Verzögerung) unverändert am Ausgang;
- konstante Gruppenlaufzeit im Durchlassbereich;
- linearer Phasengang im Durchlassbereich.
Dabei wird in Kauf genommen, dass der Amplitudenverlauf nicht so scharf wie beim Butterworth-Filter oder Tschebyscheff-Filter abknickt.
In der digitalen Signalverarbeitung können Bessel-Filter durch Wahl entsprechender Filterkoeffizienten in IIR-Filtern (rekursive Filterstruktur) realisiert werden.
Das Filter ist nach dem deutschen Mathematiker Friedrich Bessel (1784–1846) benannt.
Übertragungsfunktion
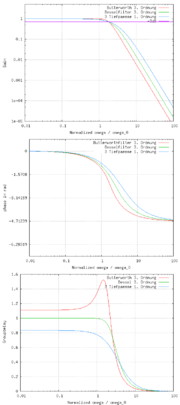 Anmerkung:Die Eckfrequenz des Butterworth-Filters und der Tiefpasskaskade wurde dem Bessel-Filter angeglichen
Anmerkung:Die Eckfrequenz des Butterworth-Filters und der Tiefpasskaskade wurde dem Bessel-Filter angeglichenDie Übertragungsfunktion ist darauf optimiert, die Gruppenlaufzeit von der Frequenz unabhängig zu machen.
Mit der Übertragungsfunktion für ein Filter n-ter Ordnung
mit
- A0 Gleichspannungsverstärkung
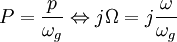 und ωg Grenzfrequenz
und ωg Grenzfrequenz
lässt sich für die Koeffizienten
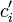 die Rekursionsformel
die Rekursionsformel-
i = 1: 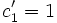
i = 2 … n: 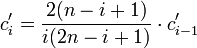
ermitteln.
Die Koeffizienten sind allerdings nicht auf die Grenzfrequenz normiert, sondern auf die Gruppenlaufzeit; d.h. bei Ω = 1 ist die Amplitude nicht um 3dB abgesunken.
Eigenschaften
Das Bessel-Filter besitzt folgende Eigenschaften:
- glatter Frequenzverlauf im Durchlassbereich
- geringe Steilheit des Amplitudengangs (geringer noch als beim Butterworth-Filter) im Bereich der Grenzfrequenz
- geringes Überschwingen bei der Sprungantwort, verringert sich mit der Ordnung
- konstante Gruppenlaufzeit im Durchlassbereich
Normalisierte Bessel-Polynome
n Bessel-Polynom 1 1 + P 2 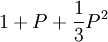
3 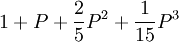
4 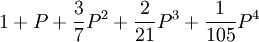
5 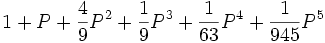
Wikimedia Foundation.