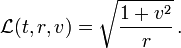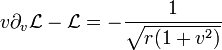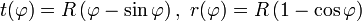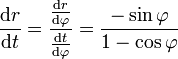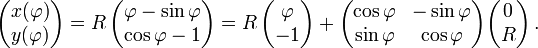- Brachystochrone
-
 Experiment: Welche Bahn ist die schnellste? (Ausstellung Elementa im Landesmuseum für Technik und Arbeit, Mannheim)
Experiment: Welche Bahn ist die schnellste? (Ausstellung Elementa im Landesmuseum für Technik und Arbeit, Mannheim)Die Brachistochrone (gr. brachistos kürzeste, chronos Zeit) ist die schnellste Verbindung zweier Punkte durch eine Bahn, auf der ein Massenpunkt unter dem Einfluss der Gravitationskraft reibungsfrei hinabgleitet. Auf der Brachistochrone-Bahn rollt eine Kugel somit schneller ans Ziel als beispielsweise auf einer Geraden zwischen dem Start- und Zielpunkt liegenden geraden Bahn, obwohl diese kürzer ist. Dabei liegt ein Punkt tiefer als der andere, aber nicht senkrecht unter dem anderen. Der Tiefpunkt der Brachistochrone-Bahn kann tiefer liegen als beide Punkte.
Gleichzeitig ist diese Kurve eine Tautochrone, d. h. von jedem Punkt der Kurve benötigt man die gleiche Zeit, um zum Tiefpunkt zu gelangen. Dieser Sachverhalt wird beim sogenannten Zykloidenpendel ausgenutzt, bei dem die Pendelmasse auf einer Tautochrone schwingt.
Inhaltsverzeichnis
Form
Das Spiegelbild der Brachistochrone bezüglich der x-Achse ist eine Zykloide.
Geschichte
Johann Bernoulli hat sich mit dem Problem des schnellsten Falles beschäftigt. Im Jahre 1696 fand er schließlich die Lösung in der Brachistochrone. Heute sieht man dies oft als die Geburtsstunde der Variationsrechnung.
Christiaan Huygens veröffentlichte 1673 in seiner Abhandlung Horologium Oscillatorium eine ganggenaue Pendeluhr mit einem Zykloidenpendel, bei dem er sich die Tatsache zunutze machte, dass die Evolute der Zykloide selber wieder eine Zykloide ist. Der Vorteil der Ganggenauigkeit wird jedoch durch die erhöhte Reibung wettgemacht.
Funktion
Die Brachistochrone lässt sich bequem in einer Parameterdarstellung beschreiben, das heißt, man kann ihre Punkte als Ortsvektor darstellen, der sich mit einem Parameter ändert. Als Funktion des Winkels
 (im Bogenmaß), um den sich das Rad mit Radius R beim Abrollen gedreht hat, sind die x- und y-Koordinaten:
(im Bogenmaß), um den sich das Rad mit Radius R beim Abrollen gedreht hat, sind die x- und y-Koordinaten:Hilfreich für das Verstehen dieser Kurve ist: Der Radius mal dem Winkel „Berührungspunkt des Kreises-Kreismittelpunkt-Brachistochronenpunkt“ ist die bereits abgerollte Strecke.
Herleitung
Betrachten wir in der x-y-Ebene eine Kurve y(x), längs welcher der Massepunkt vom Start (x,y) = (0,0) mit fortlaufender Zeit t zum Ziel
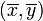 gleite.
gleite.Er hat die kinetische Energie
und die potentielle Energie
Dabei ist y die Höhe im Gravitationsfeld und g die Schwerebeschleunigung.
Gleitet der anfänglich ruhende Massepunkt vom Ursprung los, so ist längs seiner Bahn die Gesamtenergie erhalten und hat den anfänglichen Wert Null,
Dies kann nach
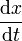 aufgelöst werden. Die Ableitung der Umkehrfunktion, t(x), die angibt, wie spät es ist, wenn das Teilchen den Ort (x,y(x)) durchläuft, ist hierzu invers
aufgelöst werden. Die Ableitung der Umkehrfunktion, t(x), die angibt, wie spät es ist, wenn das Teilchen den Ort (x,y(x)) durchläuft, ist hierzu inversIntegrieren wir über den x-Bereich von 0 bis
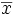 , so ergibt sich die zu minimierende Laufzeit T als Funktional der Bahnkurve y(x)
, so ergibt sich die zu minimierende Laufzeit T als Funktional der Bahnkurve y(x)Um an die bei physikalischen Variationsproblemen üblichen Bezeichnungen anzuschließen, nennen wir die Integrationsvariable
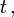 bezeichnen − y mit r und minimieren einfachheitshalber das mit
bezeichnen − y mit r und minimieren einfachheitshalber das mit 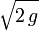 multiplizierte Funktional. Wir minimieren also die Wirkung
multiplizierte Funktional. Wir minimieren also die Wirkungmit Lagrangefunktion
Da die Lagrangefunktion nicht vom Integrationsparameter, der Zeit t abhängt, ist die nach dem Noether-Theorem zugehörige Energie
auf der Bahn r(t) erhalten, für die W[r] minimal wird.
Die Funktion r(t) erfüllt also mit einer positiven Konstanten R die Gleichung
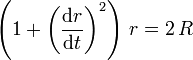 oder
oder 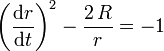
wie ein Teilchen, das im Keplerpotential
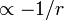 senkrecht aus der Gipfelhöhe
senkrecht aus der Gipfelhöhe 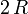 fällt.
fällt.Statt diese Gleichung mit getrennten Veränderlichen nach
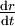 aufzulösen und zu integrieren, bestätigt man einfach, dass
aufzulösen und zu integrieren, bestätigt man einfach, dasseine parametrische Lösung dieser Gleichung ist, wobei man
ausnutzt.
Also ist die gesuchte Bahn (x,y(x)) parametrisch gegeben durch
Dabei wird an der letzten Zerlegung deutlich, dass die Bahn y(x) sich aus den Ortsvektoren
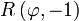 der Nabe eines Rades mit Radius R zusammensetzt, das unter der x-Achse rollt plus dem Speichenvektor, der anfänglich nach oben zeigt und mit dem Winkel
der Nabe eines Rades mit Radius R zusammensetzt, das unter der x-Achse rollt plus dem Speichenvektor, der anfänglich nach oben zeigt und mit dem Winkel  gedreht wird. Die Kurve ist die Bahn eines Randpunktes eines rollenden Rades.
gedreht wird. Die Kurve ist die Bahn eines Randpunktes eines rollenden Rades.Weblinks
Wikimedia Foundation.


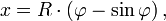
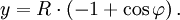
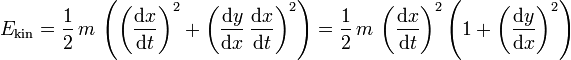
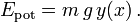
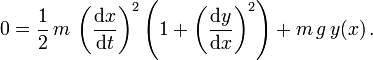
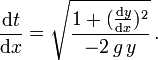
![T[y]=\frac{1}{\sqrt{2\,g}}\int_0^{\overline{x}}\mathrm d x\,\sqrt{\frac{1+(\frac{\mathrm d y}{\mathrm d x})^2}{-y}}\,.](/pictures/dewiki/53/5a9684873f8ed996c52f96a33927e1c1.png)
![W[r]=\int\mathrm d t\,\sqrt{\frac{1+(\frac{\mathrm d r}{\mathrm d t})^2}{r}}\,.](/pictures/dewiki/50/20fbce6f8dc678c4fccc1e4f9e762fb9.png)