- Parameterdarstellung
-
Unter einer Parameterdarstellung (auch Parametrisierung oder Parametrierung) einer Kurve versteht man in der Mathematik eine Darstellung, bei der die Punkte der Kurve über einen einzigen Parameter abgelaufen werden können, im Gegensatz zur impliziten Beschreibung durch eine Gleichung, beispielsweise F(x,y)=0. (Analog geht man bei der Parametrisierung von Flächen bzw. höherdimensionalen Gebilden vor, s.u.) Bei einer Parameterdarstellung ist es leicht, einzelne Punkte zu erhalten, umgekehrt fällt es bei einer Gleichungsdarstellung leicht, zu entscheiden, ob ein vorgegebener Punkt zu dem Objekt gehört oder nicht. Die Parameterdarstellungen eines geometrischen Objekts sind nicht eindeutig, es gibt beispielsweise mehrere Wege, die als Bild eine gewisse Kurve haben.
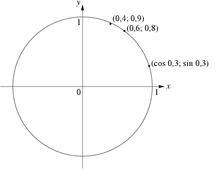
Ein Beispiel ist die Beschreibung des Einheitskreises in der Ebene: eine Parameterdarstellung wäre
 ,
,
eine Gleichung wäre
 .
.
So kann man aus der ersten Darstellung unmittelbar Punkte auf der Kreislinie erhalten, beispielsweise (cos 0,3; sin 0,3). Umgekehrt kann man an der zweiten Beschreibung unmittelbar ablesen, dass (0,6; 0,8) ein Punkt auf der Kreislinie ist, (0,4; 0,9) jedoch nur im Rahmen der Zeichengenauigkeit, da 0,4²+0,9²=0,97 ≠1 gilt.
Inhaltsverzeichnis
Parameterdarstellungen von Geraden und Ebenen
Unter der Parameterdarstellung (oder auch Parameterform) einer Geradengleichung oder einer Ebenengleichung versteht man die Form
 (Geradengleichung)
(Geradengleichung)
bzw.
 (Ebenengleichung),
(Ebenengleichung),
mit den reellen Parametern λ und μ. Der Vektor
 ist der Ortsvektor eines Punktes P0 auf der Geraden bzw. Ebene. Während
ist der Ortsvektor eines Punktes P0 auf der Geraden bzw. Ebene. Während  in der Geradengleichung ein Richtungsvektor ist, nennt man
in der Geradengleichung ein Richtungsvektor ist, nennt man  und
und  in einer Ebenengleichung Spannvektoren. Nachstehend ist dies an einer Ebene erläutert:
in einer Ebenengleichung Spannvektoren. Nachstehend ist dies an einer Ebene erläutert:Die Richtungsvektoren spannen ein affines Koordinatensystem auf (durch das blaue Koordinatennetz innerhalb der Ebene angedeutet), wobei λ und μ die affinen Koordinaten darstellen. Ein Punkt Q der Ebene kann erreicht werden, indem man vom Koordinatenursprung aus zunächst Vektor
 durchläuft und dann λ-mal Vektor
durchläuft und dann λ-mal Vektor  und μ mal Vektor
und μ mal Vektor  . Im abgebildeten Beispiel ist λ = 2 und μ = 3:
. Im abgebildeten Beispiel ist λ = 2 und μ = 3: .
.
Der Punkt Q hat dann die affinen Koordinaten (2|3). Zugleich hat er natürlich kartesische Koordinaten. Sind beispielsweise P0(4|-6|3) der Ausgangspunkt, sowie
 und
und 
die Richtungsvektoren, so hat die Ebene die Gleichung:
 .
.
Der Ortsvektor von Q ist dann
und Q hat die kartesischen Koordinaten Q(-4|1|4).
Reguläre Parameterdarstellungen
Eine differenzierbare Parameterdarstellung einer Kurve heißt regulär, wenn ihre Ableitung nirgendwo verschwindet; sie muss nicht notwendigerweise injektiv sein. Allgemein heißt eine differenzierbare Parameterdarstellung regulär, wenn sie eine Immersion ist, das heißt wenn ihre Ableitung überall injektiv ist (das heißt ihr Rang ist größer gleich der Dimension des Urbilds).
Verallgemeinerung auf höhere Dimension
Die Verallgemeinerung ist naheliegend: Es sei
 eine „Karte" einer d-dimensionalen differenzierbaren Mannigfaltigkeit
eine „Karte" einer d-dimensionalen differenzierbaren Mannigfaltigkeit  . Die Karte ist gegeben durch eine n-dimensionale differenzierbare Parametrisierung: Für Punkte P in
. Die Karte ist gegeben durch eine n-dimensionale differenzierbare Parametrisierung: Für Punkte P in  gilt also:
gilt also:  mit differenzierbaren Funktionen ui.
mit differenzierbaren Funktionen ui.Für eine beliebige Funktion f(P) der Punkte P der Mannigfaltigkeit gilt dann für die Ableitung in Richtung des Tangentialvektors einer Kurve auf
 , die auf der Karte
, die auf der Karte  den Kurvenparameter λ hat:
den Kurvenparameter λ hat: 
Dieses Ergebnis ist wegen der Kettenregel unabhängig von der gewählten Parametrisierung.[1]
Einzelnachweise
- ↑ W. Maak, Differential- und Integralrechnung, Göttingen, Vandenhoek &Ruprecht, 1969
Weblinks
Wikimedia Foundation.

 heißen)
heißen)