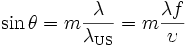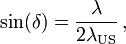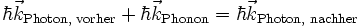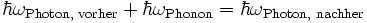Braggzelle

Ein akustooptischer Modulator (AOM) ist ein optisches Bauelement, mit dem Lichtstrahlen (meist Laserstrahlen) manipuliert werden können. In einfachster Anwendung kann ein AOM als Schalter eingesetzt werden, der sehr schnell (< 10 ns) zwischen Blockieren und Durchlassen schalten kann, also um mehrere Größenordnungen schneller als ein mechanischer Schalter. Weiterhin ist eine schnelle Modulation der Lichtintensität möglich, eine Verstimmung der Wellenlänge bei monochromatischem Licht über einen geringen Bereich sowie die Selektion von Wellenlängen bei polychromatischem Licht.

Hierzu wird in einem transparenten Festkörper ein optisches Gitter erzeugt, an dem der Lichtstrahl gebeugt wird. Da die dafür verantwortlichen Schallwellen meist über den Piezoeffekt elektrisch erzeugt werden, ist eine sehr rasche elektrische Beeinflussung des Lichtstrahls möglich. Akustooptische Modulatoren, die zur Ablenkung des Lichts eingesetzt werden, sind auch als Braggzellen bekannt.

Funktionsweise eines akustooptischen Modulators

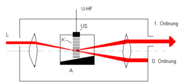
Die Ablenkung des Lichts in einem akustooptischer Modulator funktioniert nach dem Prinzip der Beugung von Licht, wie es z. B. bei einem optischen Gitter bzw. Beugungs - Transmissionsgitter der Fall ist.

Prinzip eines AOMs

Ein akustooptischer Modulator besteht aus einem durchsichtigen Festkörper, Glas oder ein Kristall, an dem zur Erzeugung von Schallwellen an einem Ende ein Piezoelement angebracht wird, und am anderen Ende befindet sich ein Schallabsorber, um Reflexionen und stehende Wellen zu vermeiden. Das Piezoelement arbeitet mit Frequenzen im Ultraschallbereich (~ 50 MHz - 1 GHz).

Beim Durchlaufen der Schallwelle durch den Kristall bewirkt diese eine periodische Dichtemodulation und damit eine periodische Brechzahlmodulation. Akustooptische Modulatoren nutzen Schallwellen zur Modulation der Brechzahl in einem transparenten Kristall. Typische Stoffe für solch ein Kristall sind u. a. LiNbO₃ oder PbMoO₄. Da die Ultraschallwelle ein bewegtes Gitter erzeugt, erleidet die Frequenz des abgelenkten Lichtes eine geringe Frequenzverschiebung durch den Doppler-Effekt. Diese ist aber im Verhältnis zur Frequenz des Lichts sehr klein, weil die Ultraschall-Frequenz (≈10⁸ Hz} wesentlich kleiner als die Frequenz des Lichts (>10¹⁴ Hz) ist.

Der Abstand der „Linien“ dieses Gitters ist gleich der Wellenlänge λ_US der Ultraschall-Welle und lässt sich über die Schallgeschwindigkeit υ und die Frequenz f berechnen, mit

λ_US = υ / f

Typische Schallgeschwindigkeiten in solchen Kristallen betragen um die 3700 - 4300 m/s. Bei einer Frequenz von ~ 200 MHz ergeben sich Gitterkonstanten von 18,5 µm - 21,5 µm. Dies sind typische Werte, hängen jedoch von der verwendeten Ultraschallfrequenz, dem verwendeten Medium und dessen Schallgeschwindigkeit ab.

Berechnung der Beugungswinkel

Wenn (monochromatisches) Licht senkrecht zur Ausbreitungsrichtung des Ultraschalls, also parallel zu den Wellenfronten auf dieses bewegte Gitter trifft, wird es nach der Bragg-Bedingung gebeugt. Ausgedrückt mit den bereits verwendeten Variablen bedeutet dies für den Winkel θ, um den der Lichtstrahl abgelenkt wird

$\sin \theta = m\frac{\lambda}{\lambda_\mathrm{US}} = m\frac{\lambda f}{\upsilon}$

wobei λ für die Wellenlänge des verwendeten Lichtes steht, und m die Beugungsordnung beschreibt.

Bragg-Beugung an mit Ultraschall erzeugtem Gitter

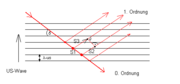
Die Wege benachbarter Teilwellen müssen sich für die erste Ordnung um λ unterscheiden, damit sich Interferenzmaxima ergeben. Im symmetrischen Fall (siehe Abbildung, Ablenkung um 2δ) muss daher für die erste Beugungsordnung S1 + S2 − S3 = λ sein. Mit Hilfe der Trigonometrie liefert eine einfache Rechnung dafür die Bragg-Bedingung:

$\sin(\delta)=\frac{\lambda}{2\lambda_\mathrm{US}}\,,$

wobei sin(δ) dem Glanzwinkel des einfallenden Lichtbündels entspricht.

Eine andere, dazu äquivalente Betrachtungsweise betrachtet die Schallwelle im Festkörper als Phononen, die mit den Photonen des Lichts wechselwirken. Die Ablenkung des Lichts kommt dadurch zustande, dass der Impuls der Phononen zum Impuls der Photonen vektoriell addiert wird:

$\hbar \vec{k}_\text{Photon, vorher} + \hbar \vec{k}_\text{Phonon} = \hbar \vec{k}_\text{Photon, nachher}$

Hierbei ist 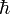$\hbar$ das durch 2π dividierte Plancksche Wirkungsquantum und k der Wellenvektor der Photonen bzw. Phononen. In dieser Betrachtungsweise folgt aus der Energieerhaltung, dass sich durch die Wechselwirkung die Frequenz des Lichts um die Frequenz der Schallwelle ändert:

$\hbar \omega_\text{Photon, vorher} + \hbar \omega_\text{Phonon} = \hbar \omega_\text{Photon, nachher}$

Hier ist ω die Kreisfrequenz, also das 2π-fache der Frequenz des Lichts (Photonen) bzw. der Schallwelle (Phononen).

Anwendungen

Die Anwendungen lassen sich in die Bereiche schnelles Schalten, periodische Verluste, Ablenkung, Frequenzverschiebung sowie Frequenzselektion unterteilen:

Schnelles Schalten

• Q-Switch in gepulsten Lasern.
• Blanking bei scannenden Verfahren wie bestimmte Verfahren der Fotolithografie oder Lasershows.

Periodische Verluste

• Einbringen periodischer Verluste in einen Laserresonator, zur aktiven Modenkopplung des Lasers. Sorgt für gepulsten Betrieb.

Ablenkung

• Elektrisch steuerbare Ablenkung eines Laserstrahls, z. B. für automatisches Justieren der Strahlposition. Im besten Fall hat das dafür verwendete Maximum erster Ordnung (m = 1) über 90% der Strahlintensität; der Rest geht verloren (nicht abgelenkt oder höhere Ordnungen)
• Intensitätsvariation des Laserstrahls durch Ablenkung in einen Absorber. Dies beruht darauf, dass bei geringer Intensität der Schallwelle der abgelenkte Anteil des Strahls proportional zur Schallintensität ist.

Frequenzverschiebung

• Frequenzverschiebung des Laserlichts für Heterodyn-Interferometer.
• Frequenzverschiebung des Laserlichts für die Erzeugung laufender Interferenzmuster zwischen dem ursprünglichen Laserstrahl und dem durch den AOM frequenzverschobenen Laserstrahl.
• Frequenzverschiebung des Laserlichts für Anwendungen in der hochauflösenden Spektroskopie und für Manipulation von Atomen in Ionenfallen.

Frequenzselektion

• Auswahl der Farbe für mehrfarbige Lasershows.

Literatur

• Naumann, Schröder: Bauelemente der Optik. Taschenbuch der technischen Optik. Fachbuchverlag Leipzig
• Frank L. Pedrotti, Leno S. Pedrotti, Werner Bausch: Optik für Ingenieure. Grundlagen. Springer, Berlin
• Helmbrecht Bauer: Lasertechnik: Grundlagen und Anwendungen. Vogel-Verlag, Würzburg

Weblink

Einführung in die Akusto-Optik (PDF, englisch)

Acousto-optic modulators (englisch)

Siehe auch

Optisches Gitter, Phasenmaske, Modulator