Kreisfrequenz

Die Kreisfrequenz ω ist eine physikalische Größe der Schwingungslehre. Der Zusammenhang der Kreisfrequenz mit der Periodendauer T und der Frequenz f einer Schwingung ist gegeben durch:

$\omega = \frac{2\pi}{T} = 2\pi f$

Eine harmonische Schwingung lässt sich allgemein beschreiben durch

$x(t) = x_o \ \sin(\omega t + \varphi_0)$

Bei Vorgängen oder Signalen mit veränderlicher Frequenz, ist die momentane Kreisfrequenz die Änderungsrate des Phasenwinkels:

$\omega = \frac{\text{d}\varphi}{\text{d}t}$

Kennkreisfrequenz und Eigenkreisfrequenz

Schwingfähige Systeme werden durch die Kennkreisfrequenz und die Eigenkreisfrequenz beschrieben. Ein ungedämpftes frei schwingendes System schwingt mit seiner Kennkreisfrequenz ω₀, ein gedämpftes System ohne äußere Anregung schwingt mit seiner Eigenkreisfrequenz ω_d. Die Eigenkreisfrequenz eines gedämpften Systems ist stets kleiner als die Kennkreisfrequenz. Die Kennkreisfrequenz wird in der Mechanik auch als ungedämpfte Eigenkreisfrequenz bezeichnet.

Für das Beispiel eines elektrischen Schwingkreises gilt mit dem Widerstand R, der Induktivität L und der Kapazität C für die Kennkreisfrequenz:

$\omega_0 = \frac{ 1} {\sqrt {LC}}$

Für ein Federpendel mit der Federsteifigkeit c, der Masse m und der Dämpfungskonstanten d gilt für die Kennkreisfrequenz:

$\omega_0 = \sqrt {\frac c m}$

und mit der Abklingkonstante δ = R / (2L) bzw. δ = d / (2m) für die Eigenkreisfrequenz:

$\omega_d = \sqrt{\omega_0^2 - \delta^2}$.

Weitere Beispiele siehe Torsionspendel, Wasserpendel, Fadenpendel.

komplexe Kreisfrequenz

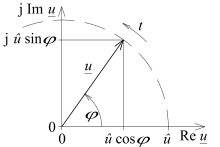Zeigerdarstellung einer harmonischen Schwingung in der komplexen Ebene (am Beispiel einer Wechselspannung $\underline{u}$) mit dem zeitabhängigen Argument φ = ωt + φ₀.

Aus der komplexen Zeigerdarstellung einer harmonischen Schwingung

$\underline{x}(t) = x_0 \ e^{i \omega t}$

ergibt sich mit dem üblichen Ansatz

$\underline{x}(t) = x_0 \ e^{s t}$

die Verallgemeinerung zur komplexen Kreisfrequenz s = σ + iω mit dem Realteil σ und der Kreisfrequenz ω. Durch die komplexe Kreisfrequenz s kann nicht nur eine konstante harmonische Schwingung mit σ = 0 dargestellt werden, sondern auch eine gedämpfte Schwingung mit σ < 0 und eine angeregte Schwingung mit σ > 0. ^[1]

Eine gedämpfte Schwingung kann wie folgt mit der konstanten komplexen Kreisfrequenz s als komplexer Zeiger dargestellt werden:

$\underline{x}(t) = x_o \ e^{s t} = x_o \ e^{(\sigma + i\omega_d)t} = x_o \ e^{\sigma t} e^{i\omega_d t} = x_o \ e^{\sigma t}(cos(\omega_d t) + i \sin(\omega_d t))$

Dabei ist ω_d die Eigenkreisfrequenz des schwingfähigen Systems und σ ist gleich dem negativen Wert der Abklingkonstante: σ = − δ (siehe dazu den vorhergehenden Abschnitt).

Bei der Laplacetransformation hat die komplexe Kreisfrequenz s = σ + iω eine allgemeinere Bedeutung als Variable im Bildbereich der Transformation F(s) zur Darstellung beliebiger Zeitfunktionen und Übertragungsfunktionen in der komplexen Frequenzebene ("s-Ebene").

Beliebige periodische Signale können als Fourierreihe dargestellt werden.

Einzelnachweise

1. ↑ Wolf-Ewald Büttner: Grundlagen der Elektrotechnik, Band 2. 2. Auflage. Oldenbourg, 2009, ISBN 978-3-486-58981-8, S. 215 (Eingeschränkte Vorschau in der Google Buchsuche).