- Bw*-Topologie
-
Der Satz von Krein-Šmulian, benannt nach Mark Grigorjewitsch Krein und Witold Lwowitsch Šmulian, ist ein mathematischer Satz aus der Funktionalanalysis, der ein Kriterium für die Abgeschlossenheit einer konvexen Menge bezüglich der schwach-*-Topologie darstellt.
Inhaltsverzeichnis
Formulierung des Satzes
Ist E ein Banachraum, so sei Er' die abgeschlossene r-Kugel im Dualraum von E, wobei r > 0 sei. Diese ist nach dem Satz von Banach-Alaoglu bezüglich der schwach-*-Topologie kompakt und daher abgeschlossen. Ist also
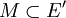 eine schwach-*-abgeschlossene Teilmenge, so sind auch die Mengen
eine schwach-*-abgeschlossene Teilmenge, so sind auch die Mengen 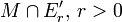 schwach-*-abgeschlossen. Der hier zu besprechende Satz sagt aus, dass für konvexe Mengen M auch die Umkehrung gilt:
schwach-*-abgeschlossen. Der hier zu besprechende Satz sagt aus, dass für konvexe Mengen M auch die Umkehrung gilt:- Satz von Krein-Šmulian: Seien E ein Banachraum und
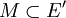 eine konvexe Menge. Wenn
eine konvexe Menge. Wenn 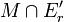 für jedes r > 0 schwach-*-abgeschlossen ist, dann ist auch M schwach-*-abgeschlossen.
für jedes r > 0 schwach-*-abgeschlossen ist, dann ist auch M schwach-*-abgeschlossen.
Bemerkungen
Ein Beispiel
Wie das folgende Beispiel zeigt, ist die Aussage des Satzes von Krein-Šmulian falsch, wenn M nicht konvex ist. Dazu seien
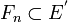 n-dimensionale Teilräume mit
n-dimensionale Teilräume mit 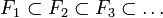 und
und 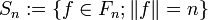 sei die Kugelfläche mit Radius n in Fn. Da diese Kugelflächen kompakt sind, gibt es ein endliches 1/n-Netz
sei die Kugelfläche mit Radius n in Fn. Da diese Kugelflächen kompakt sind, gibt es ein endliches 1/n-Netz 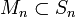 . Setze
. Setze 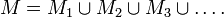 .
.Dann ist
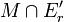 für jedes r > 0 endlich und daher schwach-*-abgeschlossen. M selbst ist aber nicht schwach-*-abgeschlossen, denn 0 liegt im schwach-*-Abschluss von M. Dazu ist zu zeigen, dass jede Menge der Form
für jedes r > 0 endlich und daher schwach-*-abgeschlossen. M selbst ist aber nicht schwach-*-abgeschlossen, denn 0 liegt im schwach-*-Abschluss von M. Dazu ist zu zeigen, dass jede Menge der Form 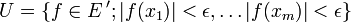 , wobei
, wobei 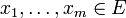 und ε > 0, ein Element aus M enthält. Wähle dazu n so groß, dass
und ε > 0, ein Element aus M enthält. Wähle dazu n so groß, dass 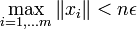 und n > m. Wegen letzterem gibt es aus Dimensionsgründen ein
und n > m. Wegen letzterem gibt es aus Dimensionsgründen ein 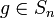 mit
mit 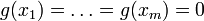 . Wähle nun ein
. Wähle nun ein 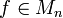 mit
mit 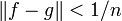 . Dann ist
. Dann ist 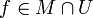 , denn
, denn 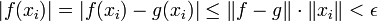 für alle
für alle 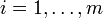 .
.Die bw*-Toplogie
Man erkläre eine Menge
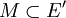 als abgeschlossen, wenn der Durchschnitt
als abgeschlossen, wenn der Durchschnitt 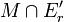 für jedes r > 0 schwach-*-abgeschlossen ist. Leicht überlegt man sich, dass dadurch eine Topologie, die sogenannte bw*-Topologie, definiert ist. Wie obiges Beispiel zeigt, ist diese Topologie im Falle unendlich-dimensionaler Banachräume echt feiner als die schwach-*-Topologie. Der Satz von Krein-Šmulian kann nun wie folgt umformuliert werden:
für jedes r > 0 schwach-*-abgeschlossen ist. Leicht überlegt man sich, dass dadurch eine Topologie, die sogenannte bw*-Topologie, definiert ist. Wie obiges Beispiel zeigt, ist diese Topologie im Falle unendlich-dimensionaler Banachräume echt feiner als die schwach-*-Topologie. Der Satz von Krein-Šmulian kann nun wie folgt umformuliert werden:- Seien E ein Banachraum und
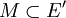 eine konvexe Menge. Dann stimmen der schwach-*-Abschluss und der bw*-Abschluss von M überein.
eine konvexe Menge. Dann stimmen der schwach-*-Abschluss und der bw*-Abschluss von M überein.
Quellen
- M. M. Day: Normed Linear Spaces Springer-Verlag GmbH, dritte Auflage (1973) ISBN 3540061487
- Satz von Krein-Šmulian: Seien E ein Banachraum und
Wikimedia Foundation.
