Konvexe Menge

eine konvexe Menge

eine nichtkonvexe Menge

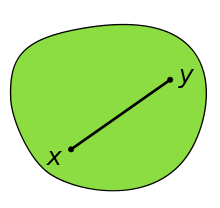
In der Mathematik heißt eine geometrische Figur oder allgemeiner eine Teilmenge eines euklidischen Raums konvex, wenn für je zwei beliebige Punkte die zur Menge gehören, auch stets deren Verbindungsstrecke ganz in der Menge liegt. Dies garantiert, dass die Menge an keiner Stelle eine (konkave) Einbuchtung hat.

Geschichte und Anwendung

Die Theorie der konvexen Mengen begründete Hermann Minkowski in seinem Werk Geometrie der Zahlen, Leipzig 1910. Anwendung finden konvexe Mengen z.B. in der konvexen Optimierung oder der Computeranimation, wo konvexe Polytope in verschiedener Hinsicht einfacher zu handhaben sind als Nichtkonvexe.

Definition für Vektorräume

Eine Teilmenge M eines reellen oder komplexen Vektorraum V heißt konvex, wenn für alle $a,b\in M$ und für alle $\lambda \in \R$ mit $0\leq\lambda\leq1$ stets gilt:

$\lambda a+(1-\lambda)b\in M.$

Diese Definition basiert auf der Parameterdarstellung der Verbindungsstrecke zwischen a und b:

$\overline{ab} := \{ \lambda a+(1-\lambda)b\mid\lambda \in \R,0\leq\lambda\leq1\}.$

Tatsächlich schließt obige Definition auch Objekte mit planaren Rändern wie Quadrate mit ein, die man umgangssprachlich nicht unbedingt als konvex bezeichnen würde.

Konkav vs. nichtkonvex

Beispiele für nichtkonvexe Figuren der Ebene

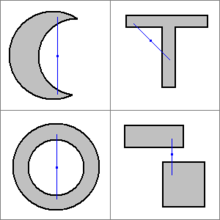
Eine Menge, die nicht konvex ist, wird nichtkonvex genannt. Dazu müssen nur zwei Punkte der Menge existieren, deren Verbindungsstrecke an mindestens einem Punkt nicht zur Menge gehört. Teilweise wird dafür auch die Bezeichnung konkave Menge verwendet, was jedoch irreführt, denn konkav ist nicht die Negation von konvex.

Manche Autoren definieren eine Teilmenge als konkav, wenn ihr Komplement konvex ist. Mit dieser Definition sind Halbebenen gleichzeitig konvex und konkav und es gibt (außer der leeren Menge) keine beschränkte, konkave Teilmenge des $\R^n$.

Beispiele

• Jeder Vektorraum, der $\R$ enthält, ist konvex, ebenso Halbebenen und Halbräume.
• Beispiel-Teilmengen des anschaulichen euklidischen Raumes:
  • Die leere Menge und jede einelementige Menge sind konvex.
  • Strecken und Geraden
  • jede Dreiecksfläche und alle regelmäßigen Polygonflächen sind konvex.
  • Kreisscheiben und Kugeln sind konvex.
  • Unter den Vierecken sind z. B. die Parallelogramme konvex, während es Trapeze und Drachenvierecke gibt, die nichtkonvex sind, wie das verschränkte Trapez oder das Pfeilviereck.
  • Würfel, Platonische Körper und Spate sind konvex.
  • Die Teilmenge die über- bzw. unterhalb des Graphen einer konvexen bzw. konkaven Funktion liegt, ist konvex.
  • Ein Torus (Donut) ist nicht konvex.
  • Der Rand einer konvexen Menge ist im Allgemeinen nichtkonvex.

Eigenschaften

• Jede nichtleere konvexe Teilmenge eines reellen oder komplexen Vektorraums ist zusammenhängend, auf einen Punkt kontrahierbar und kann somit keinerlei Löcher haben.

• Der Durchschnitt beliebig (auch unendlich) vieler konvexer Mengen ist konvex. Somit bilden die konvexen Teilmengen eines Vektorraumes ein Hüllensystem. Die Vereinigung konvexer Mengen ist hingegen im Allgemeinen nicht konvex.

• Die konvexe Hülle einer Menge ist die kleinste konvexe Obermenge. Sie ist der Durchschnitt aller konvexen Mengen, in denen sie enthalten ist.

• In lokalkonvexen Räumen ist eine kompakte konvexe Menge M der Abschluss der Konvexkombinationen ihrer Extremalpunkte (Satz von Krein-Milman). Dabei ist ein Extremalpunkt ein Punkt, der nicht zwischen zwei Punkten aus M liegt.

• Jede konvexe Menge ist sternförmig, derart, dass jeder Punkt als Sternzentrum gewählt werden kann.

Verallgemeinerungen

Allgemein genügen für die sinnvolle Definition von Konvexität schon erheblich schwächere Voraussetzungen an die Geometrie, die auf M gilt, man braucht aus Hilberts Axiomensystem der euklidischen Geometrie lediglich die Axiome der Verknüpfung und die der Anordnung. Die Konvexität hängt insbesondere von der Definition einer geraden Verbindungsstrecke ab. So ist die Halbebene, die durch $\{(x,y)\in\mathbb R^2\mid x+y \leq 0\}$ definiert wird konvex in der euklidischen Ebene, aber nichtkonvex in der Moulton-Ebene: Beispielsweise läuft die „Gerade“ zwischen ( − 1,1) und (1, − 1) über den (nicht in der Menge enthaltenen) Punkt $(0,\tfrac{1}{3})$. Siehe auch kollinear.

Je nach mathematischem Kontext werden unterschiedliche Verallgemeinerungen benutzt, die auch teilweise nicht kohärent sind.

Konvexitätsraum

Folgende Axiomatik verallgemeinert die grundlegenden Eigenschaften konvexer Mengen auf einem Niveau, das vergleichbar ist mit dem der Topologie.

Eine Menge X zusammen mit einer Menge von Teilmengen $\mathcal{K} \in \mathcal{P}(X)$ wird Konvexitätsraum genannt, wenn für $\mathcal{K}$ Folgendes gilt:

• die leere Menge und X selbst liegen in $\mathcal{K}$
• die Schnittmenge beliebig vieler Mengen aus $\mathcal{K}$ liegt wieder in $\mathcal{K}$
• Falls eine Teilmenge $K \subset \mathcal{K}$ total geordnet ist bezüglich Inklusion, so liegt die Vereinigung aller Mengen aus K in $\mathcal{K}$.

Dann werden die Mengen aus $\mathcal{K}$ die konvexen Mengen von X genannt.

Metrisch konvexer Raum

Ein Kreis ist metrisch konvex aber als Teilmenge des euklidischen Raums nichtkonvex.

Ein metrischer Raum (X,d) wird metrisch konvex genannt, wenn zu je zwei Punkten $x,y \in X$ stets ein (dazwischenliegender) Punkt $z \in X$ existiert, so dass in der Dreiecksungleichung Gleichheit gilt:

d(x,y) = d(x,z) + d(z,y)

Hier gilt allerdings nicht mehr, dass der Schnitt von metrisch konvexen Mengen wieder metrisch konvex wäre. So ist die Kreislinie mit der Metrik der Bogenlänge metrisch konvex, zwei abgeschlossenen Halbkreise, die bis auf ihre beiden Endpunkte x,y disjunkt sind, sind auch metrisch konvexe (Teil)mengen, ihr zweielementiger Schnitt {x,y} aber nicht.

Geodätisch konvexe Mannigfaltigkeiten

Semi-Riemannsche Mannigfaltigkeiten haben eine innewohnende Metrik, die die Geodäten der Mannigfaltigkeit festlegt. Wenn jedes Paar von Punkten in einer Umgebung durch eine einzige Geodäte der Mannigfaltigkeit verbunden werden kann, die vollständig in dieser Umgebung liegt, nennt man diese Umgebung einfach konvex. Eine riemannsche Mannigfaltigkeit heißt geodätisch konvex, wenn die global längenminimierende Kurve zwischen zwei beliebigen Punkten eine Geodäte der Mannigfaltigkeit ist.

Beispiele und Unterschiede

• Die rationalen Zahlen mit dem üblichen Abstand bilden eine metrisch konvexe Teilmenge von $\R$, die nicht konvex ist.
• Gleiches gilt für $\R^2\backslash \{ 0 \}$, was als riemannsche Mannigfaltigkeit auch nicht geodätisch konvex ist.
• Eine konvexe Teilmenge des euklisischen Raumes ist stets auch metrisch konvex, bezüglich der von der Norm induzierten Metrik. Für abgeschlossene Teilmengen gilt auch die Umkehrung.

Krümmung von Kurven

Im Zweidimensionalen kann die Krümmung einer stetig differenzierbaren Kurve in einem Punkt x₀ in Relation zum Betrachter untersucht werden:

• Liegen die benachbarten Punkte von x₀ in der gleichen Tangential-Halbebene wie der Betrachter, so ist sie dort für ihn konkav gekrümmt.
• Existiert eine Umgebung um x₀, so dass alle Punkte daraus in der anderen Tangential-Halbebene liegen, so ist die Kurve in x₀ für den Betrachter konvex gekrümmt.

Ecken werden konvex genannt, wenn alle Innenwinkel höchstens 180° betragen.

Analog kann in höheren Dimensionen die Krümmung von Hyperebenen untersucht werden, dazu muss das Objekt aber orientierbar sein.

Siehe auch

• Absolutkonvexe Menge
• Gleichmäßig konvexer Raum
• Extremalpunkt
• Konvexe Funktion
• Satz von Krein-Milman
• Satz von Minkowski
• Simplex (Mathematik)
• Trennungssatz
• Verallgemeinerte Konvexität

Literatur

• Convex set in der Encyclopaedia of Mathematics
• Otto Kerner, Joseph Maurer, Jutta Steffens, Thomas Thode, Rudolf Voller: Vieweg Mathematik Lexikon. Vieweg 1988, ISBN 3-528-06308-4, S. 159-160

Weblinks

• Convex auf PlanetMath
• Niels Lauritzen: Lectures on Convex Sets (pdf)

 Commons: (nicht)konvexe Mengen – Sammlung von Bildern, Videos und Audiodateien