3-Omega-Methode

Die 3-Omega-Methode ist eine Messmethode zur Bestimmung der Wärmeleitfähigkeiten von Volumenmaterial (das heißt feste oder flüssige Stoffe) und dünnen Schichten. Hierbei wird ein auf die Probe aufgebrachter Metallheizer periodisch erwärmt und die dadurch entstehenden Temperaturoszillationen gemessen. Aus deren Frequenzabhängigkeit können die Wärmeleitfähigkeit und thermische Diffusivität der Probe bestimmt werden. Das Verfahren geht zurück auf Prof. David Cahill^[1].

Methode

Zur Entstehung der 3-Omega-Komponente beitragende Signale.

Beispiel für den Verlauf einer ΔT-Kurve während einer 3-Omega-Messung.

Für 3-Omega-Messungen verwendete Heizerstruktur auf einer Glasprobe.

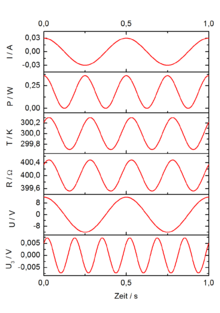
Bei der 3-Omega-Methode wird der auf die Probe gebrachte Metalldraht sowohl als Heizer, als auch als Thermometer verwendet. Die Herstellung dieses Drahtes geschieht meistens durch Mikrostrukturierung und thermisches Verdampfen. In den Metalldraht wird ein periodischer Strom mit der Kreisfrequenz ω eingespeist:

$I(t)=I_0 \cdot \cos\left(\omega t\right)$.

Die in den Heizdraht eingespeiste thermische Leistung ist dann:

$P(t)=I^2 \cdot R=I\left(t\right)^2 \cdot R=\frac{I_0^2R}{2} \cdot \left( 1+\cos\left(2 \omega t\right)\right)$,

wobei R der elektrische Widerstand des Heizers ist. Durch die eingespeiste Leistung ändert sich die Temperatur des Heizers mit der gleichen Frequenz, wie das Leistungssignal:

$T(t)=T_0 \left( t \right) + \Delta T \cdot \cos\left(2 \omega t+\varphi \right)$.

Die Amplitude ΔT und die Phasenverschiebung φ gegenüber der Einspeiseleistung ist abhängig von der Wärmeleitfähigkeit des Materials und der Frequenz ω. T₀ ist die Nullage der Temperaturschwingung und abhängig von Leistung und Ankopplung der Probe an die Umgebung. Die Temperaturoszillation des Heizdrahts führt zu einer Widerstandsoszillation desselben, die durch

$R(t)=R_0 \cdot \left[ 1 + \alpha \cdot \left( T \left( t \right)-T_0 \left( t \right) \right) \right] = R_0 + \Delta R \cdot \left[ \cos\left(2 \omega t+\varphi \right) \right]$

und

$\Delta R=\alpha \cdot R_0 \cdot \Delta T$

gegeben ist. Hierbei ist α der Temperaturkoeffizient des elektrischen Widerstands des Heizers, R₀ der Widerstand bei der Temperatur T₀ und ΔR die Amplitude der Widerstandsozillation. Aus diesem Zusammenhang und der ersten Gleichung kann nun die über den Heizdraht gemessene Spannung berechnet werden:

$\begin{align} U \left( t \right)&=R \left( t \right) \cdot I \left( t \right) \\ &=\left[ R_0+\Delta R \cos \left( 2 \omega t + \varphi \right) \right] \cdot I_0 \cos \left( \omega t \right) \\ &=R_0 I_0 \cos \left( \omega t \right) + \Delta R I_0 \cdot \cos \left( 2 \omega t + \varphi \right) \cos \left( \omega t \right) \\ &= R_0 I_0 \cos \left( \omega t \right) + \Delta R I_0 \cdot \frac 1 4 \left ( e^{i 2\omega t +i\varphi} + e^{-i 2\omega t -i\varphi}\right ) \cdot \left ( e^{i \omega t} + e^{-i \omega t}\right )\\ &= R_0 I_0 \cos \left( \omega t \right) + \Delta R I_0 \cdot \frac 1 4 \left ( e^{i 3\omega t +i\varphi} + e^{-i \omega t -i\varphi} + e^{i \omega t + i \varphi} + e^{-3i \omega t -i \varphi}\right )\\ &= R_0 I_0 \cos \left( \omega t \right) + \frac {\Delta R I_0} 2 \cdot \left[ \cos\left( 3\omega t +\varphi \right) + \cos\left( \omega t +\varphi \right)\right] \end{align}$.

Im Spannungssignal ist demnach eine Komponente mit der Frequenz 3ω zu beobachten, die die Amplitude

$U_{3\omega}=\frac {\Delta R I_0} 2=\frac {\alpha \cdot R_0 \cdot \Delta T \cdot I_0} 2$

besitzt, proportional zur Temperaturamplitude des Heizers ΔT ist und damit zur Messung der Temperaturamplitude geeignet ist. Um die Phaseninformation der Temperaturoszillation nicht zu verlieren, kann man ΔT als komplexe Größe betrachten, indem man den Phasenfaktor hinzu multipliziert. Mit modernen Lock-in-Verstärkern ist es möglich, die 3-Omega-Komponente des Spannungssignals und die Phasenabhängigkeit herauszufiltern und zu messen.

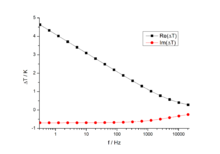
Zur Bestimmung der Wärmeleitfähigkeit der Probe wird ein Zusammenhang zwischen der Temperaturoszillation ΔT und der Wärmeleitfähigkeit benötigt. Für ein halbunendlich ausgedehntes Volumenmaterial und einen unendlich schmalen Heizer gibt es folgende Näherung^[1]:

$\Delta T(r)= \frac P {\pi l \kappa} \left[ \ln \left( 2 \right) + \frac 1 2 \ln \left( 2 \omega \right) - \gamma + \frac 1 2 \ln \left( \frac D {r^2} \right) - i \frac \pi 4 \right]$.

Hierbei ist P die eingespeiste Leistung, l die Länge des Heizdrahtes, κ die Wärmeleitfähigkeit der Probe, γ die Euler-Mascheroni-Konstante und D die thermische Diffusivität. Insbesondere ist der Realteil von ΔT proportional zum Logarithmus der Frequenz und die Wärmeleitfähigkeit ein Proportionalitätsfaktor. Wird die Temperaturoszillation bei verschiedenen Frequenzen gemessen, kann so die Wärmeleitfähigkeit der Probe bestimmt werden. Für Heizerbreiten im Bereich mehrerer Mikrometer ist diese Näherung in den meisten Fällen gültig.

Anwendung auf Dünnschichten

Für die Bestimmung der Wärmeleitfähigkeit von dünnen Schichten werden zwei Messungen durchgeführt: eine an dem Substrat und eine mit der zu charakterisierenden Schicht zwischen Heizer und Substrat.^[2] Wenn die Heizerbreite groß gegenüber der Schichtdicke ist und das Substrat gegenüber der Schicht eine hohe Wärmeleitfähigkeit besitzt, kann der Wärmetransport als eindimensional durch die Schicht betrachtet werden. Die Schicht ist dann ein zwischen Heizer und Substrat in Reihe geschalteter thermischer Widerstand und sorgt für eine Erhöhung der Temperaturoszillationen ΔT_f im Vergleich zur Messung ohne die Dünnschicht.

Aus dieser Erhöhung kann mit Hilfe des Fourierschen Gesetzes die Wärmeleitfähigkeit der Schicht κ_f bestimmt werden:

$\kappa_\text{f}=\frac {P \cdot d_\text{f}} {2 \cdot b \cdot l \cdot \Delta T_\text{f}}$.

Hier ist P die Heizleistung, d_f die Filmdicke, b die halbe Heizerbreite und l die Heizerlänge. Für beide Messungen sollte die Heizergeometrie identisch sein, da diese einen Einfluss auf den Verlauf der ΔT-Werte hat. Alternativ zu zwei Messungen, kann bei genauer Kenntnis des Substrats, die Messung am Substrat auch simuliert werden, was aber zu größeren Ungenauigkeiten führen kann.^[3]

Einzelnachweise

1. ↑ ^{a b} David G. Cahill, R. O. Pohl: Thermal conductivity of amorphous solids above the plateau. In: Phys. Rev. B. 35, Nr. 8, 1987, S. 4067-4073, doi:10.1103/PhysRevB.35.4067.
2. ↑ David G. Cahill, M. Katiyar, J. R. Abelson: Thermal conductivity of a-Si:H thin films. In: Phys. Rev. B. 50, Nr. 9, 1994, S. 6077-6081, doi:10.1103/PhysRevB.50.6077.
3. ↑ T. Borca-Tasciuc, A. R. Kumar, G. Chen: In: Review of Scientific Instruments. 72, Nr. 4, 2001, S. 2139-2147, doi:10.1063/1.1353189.

Literatur

Jason Randall Foley, The 3-Omega method as a nondestructive testing technique for composite material characterization, 1999