Spezifischer Widerstand

Physikalische Größe
Name	Spezifischer Widerstand
Formelzeichen der Größe	ρ
Größen- und Einheiten- system Einheit Dimension SI Ω·m M·L3/(I2·T3)
Siehe auch: elektrische Leitfähigkeit

Der spezifische Widerstand (kurz für spezifischer elektrischer Widerstand oder auch Resistivität) ist eine temperaturabhängige Materialkonstante mit dem Formelzeichen ρ (griech. rho). Er wird vor allem zur Berechnung des elektrischen Widerstands eines homogenen elektrischen Leiters genutzt. Die abgeleitete SI-Einheit ist [ρ]_SI = Ω · m (ergibt sich aus der dimensionsbezogenen Kürzung von Ω · mm²/m). Der Kehrwert des spezifischen Widerstands ist die elektrische Leitfähigkeit.

Ursache und Temperaturabhängigkeit

Verantwortlich für den spezifischen elektrischen Widerstand in reinen Metallen sind zwei Anteile, die sich gemäß der Matthiessenschen Regel überlagern:

• Stöße der Ladungsträger (hier Elektronen) mit Gitterschwingungen (Phononen); dieser Anteil ist von der Temperatur abhängig, und
• Stöße der Ladungsträger (hier Elektronen) mit Verunreinigungen, Fehlstellen und Gitterbaufehlern; dieser Anteil ist nicht von der Temperatur, sondern von der Konzentration der Gitterfehler abhängig.

Der temperaturabhängige Anteil am spezifischen Widerstand ist bei allen Leitern in einem jeweils begrenzten Temperaturbereich näherungsweise linear:

$\rho(T) = \rho(T_0) \cdot (1 + \alpha \cdot (T-T_0))$

wobei α der Temperaturkoeffizient, T die Temperatur und T₀ eine beliebige Temperatur, z. B. T₀ = 293,15 K = 20 °C, bei der der spezifische elektrische Widerstand ρ(T₀) bekannt ist (siehe Tabelle unten).

Je nach Vorzeichen des linearen Temperaturkoeffizienten unterscheidet man zwischen Kaltleitern (engl.: positive temperature coefficient of resistance, PTC) und Heißleitern (engl.: negative temperature coefficient of resistance, NTC). Die lineare Temperaturabhängigkeit gilt nur in einem begrenzten Temperaturintervall. Dieses kann bei reinen Metallen vergleichsweise groß sein. Darüber hinaus muss man Korrekturen anbringen (siehe auch: Kondo-Effekt).

Der spezifische elektrische Widerstand von Legierungen ist nur gering von der Temperatur abhängig, hier überwiegt der Anteil der Störstellen. Ausgenutzt wird dies beispielsweise bei Konstantan oder Manganin.

Spezifischer Widerstand als Tensor

Bei den meisten Materialien ist der elektrische Widerstand richtungsunabhängig (isotrop). Für den spezifische Widerstand genügt dann eine einfache skalare Größe, also eine Zahl mit Einheit.

Anisotropie beim elektrischen Widerstand findet man bei Einkristallen (oder Vielkristallen mit Vorzugsrichtung) mit weniger als kubischer Symmetrie. Die meisten Metalle haben kubische Kristallstruktur und sind schon daher isotrop. Zusätzlich hat man oft eine viel-kristalline Form ohne ausgeprägte Vorzugsrichtung (Textur). Ein Beispiel für anisotropen spezifischen Widerstand ist Graphit als Einkristall oder mit Vorzugsrichtung. Der spezifische Widerstand ist dann ein Tensor 2. Stufe, der die Elektrische Feldstärke $\vec E$ mit der Stromdichte $\vec j$ verknüpft.

$\vec E = \rho \cdot \vec j$

Zusammenhang mit dem elektrischen Widerstand

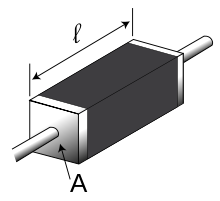
Der elektrische Widerstand eines Leiters mit einer über seine Länge konstanten Querschnittsfläche (Schnitt senkrecht zur Längsachse eines Körpers) beträgt:

Widerstand mit Kontakten an beiden Enden

$R=\rho\cdot\frac{l}{A}$

wobei R der elektrische Widerstand, ρ der spezifische Widerstand, l die Länge und A die Querschnittsfläche des Leiters ist.

Folglich kann man ρ aus der Messung des Widerstandes eines Leiterstückes bekannter Geometrie bestimmen:

$\rho={R}\cdot\frac{A}{l}$

Die Querschnittsfläche A eines runden Leiters (zum Beispiel einem Draht) errechnet sich aus dem Durchmesser d zu:

$A=\pi\cdot\frac{d^2}{4}$

Die Voraussetzung für die Gültigkeit dieser Formel für den elektrischen Widerstand R ist eine konstante Stromdichteverteilung über den Leiterquerschnitt A, das heißt, an jedem Punkt des Leiterquerschnitts ist die Stromdichte J gleich groß. Nährungsweise ist das gegeben, wenn die Länge des Leiters groß im Vergleich zu den Abmessungen seines Querschnitts ist beziehungsweise der Strom ein Gleichstrom oder niederfrequent ist. Bei hohen Frequenzen führen der Skin-Effekt und bei inhomogenen hochfrequenten Magnetfeldern und Geometrien der Proximity-Effekt zu einer inhomogenen Stromdichteverteilung.

Weitere aus dem spezifischen Widerstand ableitbare Kenngrößen sind

• der Flächenwiderstand (Schichtwiderstand einer Widerstandsschicht); Einheit Ω oder $\Omega/\Box$
• der Widerstand pro Länge eines Drahtes oder Kabels; Einheit Ω/m

Einteilung von Materialien

Der spezifische Widerstand eines Materials wird häufig für die Einordnung als Leiter, Halbleiter oder Isolator verwendet. Die Unterscheidung erfolgt anhand des spezifischen Widerstands:

• Leiter: ρ < 10⁻⁶ Ωm
• Halbleiter: ρ = 10⁻⁶…10¹⁰ Ωm
• Isolatoren oder Nichtleiter: ρ > 10¹⁰ Ωm

Wichtig ist, dass diese Einteilung keine festen Grenzen hat und daher nur als Richtlinie zu betrachten ist. Hauptgrund dafür ist die Temperaturabhängigkeit des elektrischen Widerstands, vor allem bei Halbleitern. Eine Einteilung anhand der Lage des Fermi-Niveaus ist hier sinnvoller.

Es gilt: 1 Ω · mm²/m = 10⁻⁶ Ω · m

Spezifischer Widerstand ausgewählter Materialien bei 20 °C

Material	Spezifischer Widerstand in Ω · mm2/m	Linearer Widerstands- Temperaturkoeffizient in 1/K
Akkusäure	p5041.51,5 ⋅ 104
Aluminium	p4982.652,65 ⋅ 10−2[1]	3,9 ∙ 10−3
Aluminiumoxid	p51811 ⋅ 1018
Bernstein	p52211 ⋅ 1022
Blei	p4992.082,08 ⋅ 10−1[1]	4,2 ∙ 10−3
Blut	p5061.61,6 ⋅ 106
Chromnickel	p5001.11,1	1,4 ∙ 10−4
Edelstahl (1.4301, V2A)	p4997.27,2 ⋅ 10-1[2]
Eisen	p4991.01,0 ⋅ 10−1 bis 1,5 ∙ 10−1	5,6 ∙ 10−3
Fettgewebe	p5073.33,3 ⋅ 107
Germanium	p5054.64,6 ⋅ 105
Glas	p51611 ⋅ 1016 bis 1 ∙ 1021
Glimmer	p51511 ⋅ 1015 bis 1 ∙ 1018
Gold	p4982.2142,214 ⋅ 10−2[1]	3,9 ∙ 10−3
Graphit	p50088	−2 ∙ 10−4
Gummi (Hartgummi) (Werkstoff)	p51911 ⋅ 1019
Holz (trocken)	p51011 ⋅ 1010 bis 1 ∙ 1016
Kochsalzlösung (10 %)	p5047.97,9 ⋅ 104
Kohlenstoff	p5013.53,5 ⋅ 101	−2 ∙ 10−4
Konstantan	p49955 ⋅ 10−1	5 ∙ 10−5
Kupfer (rein)	p4981.6781,678 ⋅ 10−2[1][3]	3,9 ∙ 10−3
Kupfersulfatlösung (10 %)	p50533 ⋅ 105
Meerwasser	p50555 ⋅ 105
Messing	p49877 ⋅ 10−2	1,5 ∙ 10−3
Muskelgewebe	p50622 ⋅ 106
Nichrome (Nickel-Chrom Legierung)	p5001.51,5
Nickel	p4986.936,93 ⋅ 10−2[1]	p4976.76,7 ⋅ 10−3
Papier	p51511 ⋅ 1015 bis 1 ∙ 1017
Platin	p4991.051,05 ⋅ 10−1[1]	3,8 ∙ 10−3
Polypropylenfolie	p51111 ⋅ 1011
Porzellan	p51811 ⋅ 1018
Quarz-glas	p5237.57,5 ⋅ 1023
Quecksilber	p4999.69,6 ⋅ 10−1	9 ∙ 10−4
Salzsäure (10 %)	p5041.51,5 ⋅ 104
Schwefel	p52111 ⋅ 1021
Schwefelsäure (10 %)	p5042.52,5 ⋅ 104
Silber	p4981.5871,587 ⋅ 10−2[1]	3,8 ∙ 10−3
Silizium	p5092.32,3 ⋅ 109
Stahl	p49911 ⋅ 10-1 bis 2 ∙ 10-1	5,6 ∙ 10−3
Titan	p49988 ⋅ 10−1
Wasser (destilliert)	p51011 ⋅ 1010
Wolfram	p4985.285,28 ⋅ 10−2[1]	4,1 ∙ 10−3

Literatur

Als Standardwerk für tabellarische Daten zum spezifischen (elektrischen) Widerstand empfiehlt sich:

• David R. Lide: CRC Handbook of Chemistry and Physics: A ready-reference book of chemical and physical data. 90. Auflage. CRC Taylor & Francis, Boca Raton Fla. 2009, ISBN 978-1-4200-9084-0.

Weblinks

• Virtuelles Experiment zum Spezifischen Widerstand
• Conductivity and Resistivity Values for Iron & Alloys. Collaboration for NDT Education, März 2002 (PDF-Datei, Tabelle mit spezifischem Widerstand vieler Legierungen).

Einzelnachweise

1. ↑ ^{a b c d e f g h} David R. Lide: CRC Handbook of Chemistry and Physics: A ready-reference book of chemical and physical data. 90. Auflage. CRC Taylor & Francis, Boca Raton Fla. 2009, ISBN 978-1-4200-9084-0, S. 12-41 bis 12-42.
2. ↑ http://www.alleghenyludlum.com/ludlum/Documents/302_305.pdf
3. ↑ In vielen Büchern findet sich ein Wert von ≈ 1,78 ∙ 10⁻² Ω · mm²/m; dieser Wert bezieht sich meist auf typische Kupferkabel, das heißt, sie sind nicht hochrein.