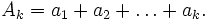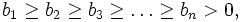Abelsche Teilsummation

In der Mathematik ist die abelsche partielle Summation (nach N. H. Abel) eine bestimmte Umformung einer Summe von Produkten jeweils zweier Zahlen.

Es seien n eine natürliche Zahl und $a_1,a_2,\ldots,a_n,b_1,b_2,\ldots,b_n$ irgendwelche Zahlen (z. B. reelle Zahlen). Dann gilt

$a_1b_1 + a_2b_2 + \ldots + a_nb_n = A_nb_n + \sum_{k=1}^{n-1}A_k(b_k-b_{k+1})$

mit

$A_k = a_1 + a_2 + \ldots + a_k.$

(Zur Notation siehe hier.)

Die Aussage besitzt eine gewisse formale Ähnlichkeit zur partiellen Integration, wenn man die Entsprechung zwischen Summen und Integralen sowie zwischen Differenzen und Ableitungen berücksichtigt. Dies motiviert die Bezeichnung.

Abelsche Ungleichung

Ist (b_k) eine monoton fallende Folge mit positiven Folgegliedern, d. h. gilt

$b_1\geq b_2\geq b_3\geq\ldots\geq b_n>0,$

und sind die Zahlen a_k beliebig reell (oder komplex), so gilt

$\bigg|\sum_{k=1}^na_kb_k\bigg|\leq b_1\cdot\max_{k=1,\ldots,n}|A_k|.$

(Zur Notation „max“ siehe größtes und kleinstes Element.)

Diese Aussage folgt direkt durch Anwendung der Dreiecksungleichung auf die rechte Seite der oben angegebenen Gleichung für die abelsche partielle Summation.

Anwendungsbeispiel

Abel benutzt die Ungleichung in seiner Arbeit (siehe Quellen), um zu beweisen, dass eine Potenzreihe

$a_0 + a_1x + a_2x^2 + \ldots,$

die für eine bestimmte positive reelle Zahl x = x₀ konvergiert, auch für jede kleinere positive Zahl x < x₀ konvergent ist und auf 0 < x < x₀ eine stetige Funktion darstellt. Der wesentliche Schritt dabei ist die Umformung

$a_mx^m + a_{m+1}x^{m+1} + \ldots = \Big(\frac x{x_0}\Big)^m\cdot a_mx_0^m + \Big(\frac x{x_0}\Big)^{m+1}\cdot a_{m+1}x_0^{m+1} + \ldots,$

und da (x / x₀)^k eine monoton fallende Folge ist, kann man die Summe auf der rechten Seite nach der abelschen Ungleichung durch

$\bigg|\frac x{x_0}\bigg|^m\cdot\sup_{k\geq m}\bigg|\sum_{\nu=m}^k a_\nu x_0^\nu\,\bigg|$

nach oben abschätzen, und die beiden Faktoren werden für großes m beliebig klein.

Quellen

• H. Heuser, Lehrbuch der Analysis, 9. Aufl., Stuttgart 1991. ISBN 3-519-22231-0
• Niels Henrik Abel, Untersuchungen über die Reihe

$1+\frac m1x+\frac{m\,.\,(m-1)}{1\,.\,2}\,.\,x^2+\frac{m\,.\,(m-1)\,.\,(m-2)}{1\,.\,2\,.\,3}\,.\,x^3+\ldots$ u.s.w.,

J. Reine Angew. Math. 1 (1829) 311–331

Die abelsche Ungleichung zusammen mit der relevanten Umformung findet sich als Lehrsatz III auf S. 314.

Weblinks

http://mathworld.wolfram.com/AbelsInequality.html