Cliquenweite

Die Cliquenweite ist ein Begriff aus der Graphentheorie und ordnet jedem ungerichteten Graphen  $G = (V, E)\,$  eine natürliche Zahl zu. Sie ist daher ein Graphparameter. Auf Graphen mit beschränkter Cliquenweite lassen sich viele NP-vollständige Probleme wie zum Beispiel UNABHÄNGIGE MENGE, HAMILTONKREIS oder CLIQUE in polynomieller Zeit lösen.

Definition

Der Begriff der Cliquenweite eines Graphen wurde erstmalig von Bruno Courcelle und Stephan Olariu eingeführt ^[1].
Für die Definition der Cliquenweite muss zunächst der Begriff des k-markierten Graphen eingeführt werden:

k-markierter Graph

• Für ein  $\, k \in \N$ sei  $\, \lbrack k \rbrack\, := \lbrace 1,\ldots,k \rbrace$
• Ein k-markierter Graph  $\ G = (V_{G}, E_{G}, lab_{G}) \$  ist ein Graph  $\ (V_{G}, E_{G})\$, dessen Knoten mit einer Markierungsabbildung  $\, lab_{G}: V_{G} \rightarrow \lbrack k \rbrack$ markiert werden
• Ein Graph mit genau einem mit $i \in \lbrack k \rbrack$ markierten Knoten wird mit $\bullet_{i}$ bezeichnet

Cliquenweite

Ein k-markierter Graph  $G \,$  hat eine Cliquenweite von höchstens k, wenn  $G \,$  in der Graphklasse $CW_{k} \,$ enthalten ist. Dabei ist $CW_{k} \,$ wie folgt definiert:

1. Der k-markierte Graph $\bullet_{i}$ ist in $CW_{k} \,$, $i \in \lbrack k \rbrack$
2. Seien  $G = (V_{G}, E_{G}, lab_{G}) \,$  und  $J = (V_{J}, E_{J}, lab_{J}) \,$  knotendisjunkte k-markierte Graphen. Der k-markierte Graph  $G \oplus J = (V', E', lab')$  ist in  $CW_{k} \,$ , mit
   
   
   1. $V' := V_{G} \cup V_{J}$
      
      
   2. $E' := E_{G} \cup E_{J}$
      
      
   3. $lab'(u) = \begin{cases} lab_{G}(u), & \text{falls } u \in V_{G},\\ lab_{J}(u), & \text{falls } u \in V_{J} \end{cases}$    $\forall u \in V'$
      
      
3. Seien $i, j \in \lbrack k \rbrack$ mit $i \neq j$ und  $G = (V_{G}, E_{G}, lab_{G}) \,$  ein k-markierter Graph. Es sind
   1. der k-markierte Graph  $\rho_{i \rightarrow j}(G) = (V_{G}, E_{G}, lab')$  in  $CW_{k}\,$  mit $lab'(u) = \begin{cases} lab_{G}(u), & \text{falls } lab_{G}(u) \neq i, \\ j, & \text{falls } lab_{G}(u) = i \end{cases}$    $\forall u \in V'$
      
      
   2. der k-markierte Graph  $\,\eta_{i, j}(G) = (V_{G}, E', lab_{G})$ in  $CW_{k}\,$  mit $E' = E_{G} \cup \lbrace \lbrace u, v \rbrace | lab(u) = i, lab(v) = j \rbrace$

Die Cliquenweite eines markierten Graphen  $G\,$  ist die kleinste natürliche Zahl  k  mit $G \in CW_{k}$ und wird mit  $cw(G)\,$  bezeichnet.

Ein Ausdruck $X\,$, der sich aus den Operationen  $\bullet_{i}$, $\oplus$, $\rho_{i \rightarrow j}$ und $\eta_{i,j}\,$, wobei $i, j \in \lbrack k \rbrack$ , zusammensetzt, wird als Cliquenweite-k-Ausdruck oder k-Ausdruck bezeichnet.

Beispiel

Der ungerichtete Graph mit 6 Knoten C₆ hat eine Cliquenweite von 3, da er sich mit den folgenden Operationen erzeugen lässt:

3-Ausdrucksbaum für die Konstruktion des C₆

Cliquenweite-Operation	Visualisierung des Graphen
$G_{1} = \bullet_{1}$
$G_{2} = \bullet_{2}$
$G_{3} = G_{1} \oplus G_{2}\,$
$G_{4} = \eta_{1,2}(G_{3})\,$
$G_{5} = G_{4} \oplus G_{4}$
$G_{6} = G_{5} \oplus \bullet_{3}$
$G_{7} = \eta_{1,3}(G_{6})\,$
$G_{8} = \rho_{3 \rightarrow 1}(G_{7})$
$G_{9} = G_{8} \oplus \bullet_{3}$
$C_{6} = \eta_{2,3}(G_{9})\,$

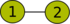
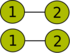
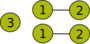
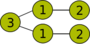
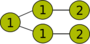
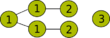
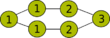
Der zugehörige 3-Ausdruck ist

    $X = \eta_{2, 3}(\rho_{3 \rightarrow 1}(\eta_{1, 3}(\eta(\bullet_{1} \oplus \bullet_{2}) \oplus \eta(\bullet_{1} \oplus \bullet_{2}) \oplus \bullet_{3})) \oplus \bullet_{3})$

Rechts ist der entsprechende 3-Ausdrucksbaum für $X\,$ abgebildet.

Cliquenweite spezieller Graphklassen

Obwohl das Bestimmen der Cliquenweite eines Graphen unter allgemeinen Voraussetzungen nicht in polynomieller Zeit möglich ist, so lässt sich die Cliquenweite von gewissen Graphen mit speziellen Eigenschaften zumindest nach oben abschätzen. Es existieren die folgenden Zusammenhänge:

• Jeder vollständige Graph hat eine Cliquenweite von höchstens 2
• Jeder Weg hat eine Cliquenweite von höchstens 3
• Auch Bäume und distanzerhaltende Graphen haben eine Cliquenweite von höchstens 3

Weiterhin ist bekannt, dass Co-Graphen eine Cliquenweite von höchstens 2 haben und dass jeder Graph mit einer Cliquenweite von höchstens 2 ein Co-Graph ist.

Zusammenhang zwischen Cliquenweite und Baumweite

Es existieren mehrere Zusammenhänge zwischen der Cliquenweite  $cw(G)\,$  und der Baumweite  $tw(G)\,$  eines ungerichteten Graphen  $G\,$.

Die folgende Aussage zeigt, dass sich  $cw(G)\,$  durch  $tw(G)\,$  nach oben abschätzen lässt^[2]:

    $cw(G) \leq 3 \cdot 2^{tw(G) - 1}$

Umgekehrt hingegen lässt sich die Baumweite eines Graphen im Allgemeinen nicht durch seine Cliquenweite beschränken, wie man sich leicht am Beispiel vollständiger Graphen überlegen kann:

Der vollständige Graph K_n mit n Knoten hat eine Baumweite von n − 1 und eine Cliquenweite von höchstens 2. Somit gilt:

    Für alle  $n\,$  mit  $n \geq 4: cw(K_{n}) < tw(K_{n})$ .

Allerdings lässt sich unter gewissen Umständen auch die Baumweite durch die Cliquenweite nach oben abschätzen.
Besitzt  $G\,$  keinen vollständig bipartiten Graphen  $K_{n, n}\,$  als Teilgraphen, so gilt die folgende Aussage^[3]:

    $tw(G) \leq 3 \cdot (n - 1) \cdot cw(G) - 1$

Zusammenhang zwischen Cliquenweite und NLC-Weite

Die Cliquenweite lässt sich sowohl nach unten als auch nach oben durch die NLC-Weite  $nlcw(G)\,$  abschätzen:

    $nlcw(G) \leq cw(G) \leq 2 \cdot nlcw(G)$

Einzelnachweise

1. ↑ Bruno Courcelle, Stephan Olariu: Upper bounds to the clique width of graphs, Discrete Applied Mathematics 101 (1–3): 77–144, 2000, doi:10.1016/S0166-218X(99)00184-5
2. ↑ Derek Corneil , Udi Rotics: On the Relationship between Clique-Width and Treewidth, Lecture Notes in Computer Science, 2001, Volume 2204/2001, 78-90, doi:10.1007/3-540-45477-2_9
3. ↑ Frank Gurski, Egon Wanke: The Tree-Width of Clique-Width Bounded Graphs without K_n,n, Lecture Notes in Computer Science, 2000, Volume 1928/2000, 221-232, doi:10.1007/3-540-40064-8_19

Literatur

• Bruno Courcelle, Stephan Olariu: Upper bounds to the clique width of graphs, Discrete Applied Mathematics 101 (1–3): 77–144, 2000, doi:10.1016/S0166-218X(99)00184-5
• Frank Gurski, Irene Rothe, Jörg Rothe, Egon Wanke: Exakte Algorithmen für schwere Graphenprobleme, Springer-Verlag, Berlin Heidelberg, 2010, ISBN 978-3-642-04499-1
• Jörg Rothe: Komplexitätstheorie und Kryptologie, Springer-Verlag, Berlin Heidelberg, 2008, ISBN 978-3-540-79744-9