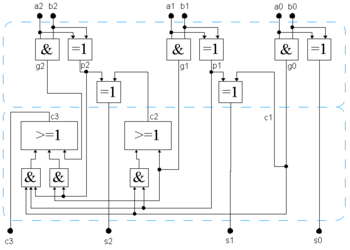
Carry-Look-Ahead-Adder

Carry-Look-Ahead-Adder

Der Paralleladdierer mit Übertragsvorausberechnung bzw. Carry-Look-Ahead-Addierer (kurz: CLA-Addierer) ist ein elektronischer Baustein zur Addition mehrstelliger Binärzahlen (siehe auch Addierwerk).

Der CLA-Addierer addiert zwei n-stellige Binärzahlen, verfügt also über 2·n Eingänge. Da das Ergebnis einen etwaigen Übertrag enthalten kann, gibt es n+1 Ausgänge.

Während beim Carry-Ripple-Addierer die Bits der beiden Summanden zwar parallel addiert werden, die etwaigen Überträge aber sequentiell von Volladdierer zu Volladdierer weitergereicht werden, ist die Laufzeit recht hoch. Der CLA-Addierer dagegen verfügt über eine spezielle Logik, die die Überträge bereits im ersten Additionsschritt ermittelt. Dies ist allerdings mit einem größeren Schaltungsaufwand verbunden.

Ein CLA-Addierer mit n Bit Wortbreite benötigt unter anderem ein Und-Gatter und ein Oder-Gatter mit n Eingängen. Logikgatter mit vielen Eingängen haben meist hohe Verzögerungszeiten beim Schalten, weshalb CLA-Addierer nur bei kleinen Wortbreiten effektiv sind.

Ein ähnlich schnell addierendes Rechenwerk stellt die Conditional Sum Addition dar.

Funktionsweise

3-Bit-Carry-Look-Ahead-Addierer

a und b sind die Summanden. g (generate: generieren, erzeugen) gibt an, ob an einer Stelle ein Übertrag erzeugt wird. p (propagate: propagieren, verbreiten) gibt an, ob an einer Stelle der Übertrag von der vorherigen Stelle weitergegeben wird oder ob der Übertrag absorbiert wird (1 = wird weitergegeben, 0 = wird absorbiert). s (sum) ist die Summe und c (carry) der Übertrag.

  • gi = ai AND bi
  • pi = ai XOR bi
  • si = pi XOR ci
  • ci+1 = gi OR pici
  • c0 = 0
  • c1 = g0 OR (p0 AND c0)
  • c2 = g1 OR (p1 AND g0) OR (p0 AND p1 AND c0)
  • c3 = g2 OR (p2 AND g1) OR (p2 AND p1 AND g0) OR (p0 AND p1 AND p2 AND c0)
  • ...

Erklärung in Worten am Beispiel c3: An der 3ten Stelle gibt es einen Übertrag, wenn die 2. Stelle einen Übertrag erzeugt, oder wenn die 2. Stelle den von der 1. Stelle erzeugten Übertrag weitergibt, oder wenn die 2. und 1. Stelle den von der 0ten Stelle erzeugten Übertrag weitergibt.

Im 3-Bit-CLA-Addierer in der Abbildung wurde c0 weggelassen, da dieses stets 0 ist. s0 ist somit immer gleich p0.

Weblinks


Wikimedia Foundation.

Игры ⚽ Нужен реферат?

Schlagen Sie auch in anderen Wörterbüchern nach:

  • Carry look-ahead adder — A carry look ahead adder is a type of adder used in digital logic. It can be contrasted with the simpler, but usually slower, ripple carry adder ( see adder for detail on ripple carry adders ). A ripple carry adder works in the same way as pencil …   Wikipedia

  • Carry — or carrying may refer to: *Carry (arithmetic), when a digit becomes bigger than limit and the extra is moved to the left **Carry flag, the equivalent in calculation in a computer *Carrying (basketball), a rule breach in basketball *Carry… …   Wikipedia

  • Carry-lookahead adder — 4 bit adder with carry lookahead A carry lookahead adder (CLA) is a type of adder used in digital logic. A carry lookahead adder improves speed by reducing the amount of time required to determine carry bits. It can be contrasted with the simpler …   Wikipedia

  • Carry-save adder — MotivationA carry save adder is a type of digital adder, used in computer microarchitecture to compute the sum of three or more n bit numbers in binary. It differs from other digital adders in that it outputs two numbers of the same dimensions as …   Wikipedia

  • Adder-subtracter — In digital circuits, an adder subtracter is a circuit that is capable of adding or subtracting numbers (in particular, binary).Below is a circuit that does adding or subtracting depending on a control signal.However, it is possible to construct a …   Wikipedia

  • Adder (electronics) — In electronics, an adder or summer is a digital circuit that performs addition of numbers.In modern computers adders reside in the arithmetic logic unit (ALU) where other operations are performed.Although adders can be constructed for many… …   Wikipedia

  • Carry-Bypass-Adder — Das Addiernetz bildet aus den Summanden a3..0 und b3..0 die Summe s3..0, carry in und carry out ermöglichen die Kaskadierung des Schaltnetzes Das Addierwerk ist die Hauptkomponente des Rechenwerks einer CPU. Das Addierwerk ermöglicht die Addition …   Deutsch Wikipedia

  • Lookahead Carry Unit — A Lookahead Carry Unit (LCU) is a logical unit in digital circuit design used to decrease calculation time in adder units and used in conjunction with carry look ahead adders (CLAs).16 bit adderBy combining four 4 bit CLAs, a 16 bit adder can be… …   Wikipedia

  • Kogge-Stone Adder — The Kogge Stone adder is a parallel prefix form carry look ahead adder. It generates the carry signals in O(log n) time, and is widely considered the fastest adder design possible. It is the common design for high performance adders in… …   Wikipedia

  • Ling adder — In electronics, an adder is a combinatorial or sequential logic element which computes the n bit sum of two numbers. The family of Ling adders is a particularly fast adder and is designed using H. Ling s equations and generally implemented in… …   Wikipedia

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”