Catalanzahl

Eugène Charles Catalan

Die Catalan-Zahlen oder catalanschen Zahlen, benannt nach dem belgischen Mathematiker Eugène Charles Catalan (1814–1894), sind eine Folge natürlicher Zahlen, die in vielen Problemen der Kombinatorik auftaucht. Die n-te Catalan-Zahl C_n ist z. B. die Anzahl der verschiedenen Möglichkeiten, ein konvexes (n+2)-Eck durch Diagonalen in Dreiecke zu zerteilen (Triangulation). Die ersten Catalan-Zahlen beginnend mit C₀ sind

1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862, … (Folge A000108 in OEIS)

Für ein Fünfeck gibt es fünf mögliche Triangulationen.

Für die Catalan-Zahlen gilt für $n\ge0$:

$C_{n}=\frac{1}{n+1}{2n \choose n}$

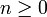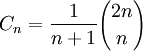
wobei 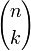${n \choose k}$ den Binomialkoeffizienten bezeichnet.

Eine Rekursionsformel lautet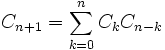

$C_{n+1}=\sum_{k=0}^n C_kC_{n-k}$ (also z. B. C₃ = C₀C₂ + C₁C₁ + C₂C₀)

und die erzeugende Funktion ist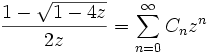

$\frac{1-\sqrt{1-4z}}{2z}=\sum_{n=0}^\infty C_nz^n$.

Weitere Interpretation für die Catalan-Zahlen

• C_{n + 1} ist die Anzahl der möglichen Beklammerungen eines Produktes, in dem n Multiplikationen vorkommen (also mit n+1 Faktoren), so dass immer nur die Multiplikation von zwei Faktoren durchzuführen ist. Es ist C₃ = 5, denn alle möglichen Beklammerungen von x₁x₂x₃x₄ sind die folgenden:
  • (x₁x₂)(x₃x₄)
  • (x₁(x₂x₃))x₄
  • x₁((x₂x₃)x₄)
  • ((x₁x₂)x₃)x₄
  • x₁(x₂(x₃x₄))

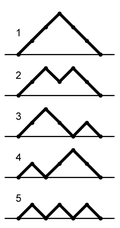
• C_n ist die Anzahl aller eindimensionalen Irrfahrten von 0 nach 2n mit Anfangs- und Endpunkt in 0, so dass sich der Pfad nie unterhalb der x-Achse befindet. Es ist wieder C₃ = 5, denn alle möglichen Pfade sind:

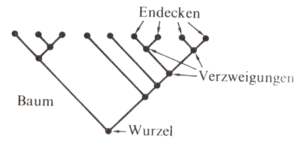
• C_n ist die Anzahl der möglichen Binärbäume, die sich aus (2n+1) Knoten bilden lassen, das heißt (n+1) Endecken/Blätter haben.

Ein Baum mit neun Endecken

Weblinks

• Catalan-Zahlen Zulassungsarbeit zum Staatsexamen