Diagonale (Geometrie)

Diagonale (von altgriech. διά dia: "durch" und γωνία gonia: "Ecke, Winkel") ist ein Begriff aus der Geometrie. Allgemein bezeichnet der Begriff gewisse Strecken, die Ecken von Flächen oder Körpern miteinander verbinden; für die präzise Definition siehe unten.

Diagonalen in der ebenen Geometrie

In der ebenen Geometrie bezeichnet man als Diagonalen die Verbindungsstrecken von nicht nebeneinander liegenden Ecken in einem Polygon (Vieleck), welches daher mind. vier Ecken haben muss.

Anzahl der Diagonalen

Die Anzahl d der Diagonalen in einem n-Eck, also in einem Vieleck mit der Eckenzahl n, beträgt $d = \frac{n(n-3)}{2}$.

Denn jede der n Ecken wird mit (n − 3) Ecken durch eine Diagonale verbunden (nicht mit sich selbst und nicht mit den beiden Nachbarecken). Durch den Nenner (Divisor) 2 in der Formel wird berücksichtigt, dass mit dieser Betrachtung bei einem vollständigen Umlauf über alle Eckpunkte jede Diagonale zweimal erzeugt würde.

Daraus ergibt sich für die Eckenzahl 3 bis 25:

n	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23	24	25
d	0	2	5	9	14	20	27	35	44	54	65	77	90	104	119	135	152	170	189	209	230	252	275

Bei einem konvexen Polygon liegen alle Diagonalen vollständig innerhalb des Polygons, bei einem konkaven Polygon mindestens eine Diagonale komplett außerhalb.

Längen von Diagonalen

Allgemein

Die Diagonallänge d von einer Ecke zur übernächsten Ecke berechnet sich aus der Länge der beiden dazwischenliegenden Seiten s₀ und s₁ und dem dazwischenliegenden Winkel ϕ₁ nach dem Kosinussatz:

$d = \sqrt{s_0^2+s_1^2-2s_0s_1\cos\varphi_1}$

Sind bei einer Diagonale für einen Teilumfang zwischen den Enden der Diagonale die Seiten und die Innenwinkel der dazwischenliegenden Ecken bekannt, so lässt sich die Diagonallänge daraus berechnen.

Bezeichnet man, von einem Diagonalenende ausgehend, die Seiten mit s_i und den jeweils davor liegenden Innenwinkel mit ϕ_i so gilt:

• Für die Diagonale über drei Seiten:

$d_3 = \sqrt{(s_0-s_1 \cdot \cos(\varphi_1) + s_2 \cdot \cos(\varphi_1+\varphi_2))^2 + (s_1 \cdot \sin(\varphi_1) - s_2\cdot \sin((\varphi_1+\varphi_2))^2}$

• Für die Diagonale über vier Seiten gilt:

$\begin{align} d_4^2 & = (s_0 - & s_1 \cdot \cos(\varphi_1) + s_2 \cdot \cos(\varphi_1+\varphi_2) - s_3 \cdot \cos(\varphi_1+\varphi_2+\varphi_3))^2\\ & + ( & s_1 \cdot \sin(\varphi_1) - s_2 \cdot \sin(\varphi_1+\varphi_2) + s_3 \cdot \sin(\varphi_1+\varphi_2+\varphi_3))^2 \end{align}$

• Allgemein für eine Diagonale über n Seiten:

$d_n =\sqrt{ \left( s_0 + \sum_{i=1}^{n-1} (-1)^i \cdot s_i \cdot \cos \left( \sum_{k=1}^{i} \varphi_k \right) \right) ^2 + \left( \sum_{i=1}^{n-1} - (-1)^i \cdot s_i \cdot \sin \left( \sum_{k=1}^{i} \varphi_k \right) \right) ^2}$

Spezialfälle

Für einige Spezialfälle existieren einfache Formeln für die Diagonalenlänge:

• Die Diagonalenlängen eines Parallelogramms mit den Seitenlängen a und b sowie dem Innenwinkel α sind:

$e = \sqrt{a^2+b^2+2ab\cos\alpha}$

und

$f = \sqrt{a^2+b^2-2ab\cos\alpha}$

• Für die Diagonalenlänge eines Rechtecks (ϕ = 90°) mit den Seitenlängen a und b gilt daher nach dem Satz des Pythagoras:

$d = \sqrt{a^2+b^2}$.

Regelmäßige Polygone

• Die Diagonalenlänge eines Quadrats mit Seitenlänge a lässt sich berechnen gemäß

$d = a\sqrt{2}$.

• Für die Diagonalenlänge eines regelmäßigen Fünfecks mit Seitenlänge a gilt

$d = \frac{a}{2} \left(1+\sqrt{5}\right)$

• Für die Diagonale über zwei Seiten im regelmäßigen Sechseck mit Seitenlänge a gilt

$d = a \frac{\sqrt{3}}{2}$.

Hauptdiagonale:

d = 2a.

Diagonalen in der Raumgeometrie

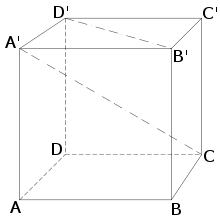
In der Stereometrie versteht man unter der Diagonale eines Polyeders eine solche Strecke, die zwei Ecken des Körpers miteinander verbindet, aber weder mit einer Kante noch mit einer Diagonale einer Seitenfläche zusammenfällt (Raum- oder Körperdiagonale).

Anzahl der Diagonalen

Um die Anzahl der Diagonalen eines Polyeders zu finden, zieht man von der Zahl der Ecken den Wert 1 ab, multipliziert den Rest mit der Anzahl der Ecken und halbiert das Produkt. Von der so erhaltenen Zahl zieht man zunächst die Anzahl sämtlicher Kanten und dann die Anzahl der Diagonalen sämtlicher Seitenflächen ab.

Bezeichnet man die Eckenzahl mit E, die Anzahl der Flächen mit F die Anzahl der Kanten mit K und die Anzahl der Ecken der Fläche Nr. i mit N_i einer so ergibt sich

$Z = \frac{E (E-1)}{2} - K - \sum_{i=1}^F \frac{N_i(N_i-3)}{2}$

Für alle Parallelepipede, z.B. Quader, ergibt sich mit

$E = 8 , \quad F = 6 , \quad K = 12 , \quad N_i = 4 \quad \forall i$:

$Z = \frac{8 (8-1)}{2} - 12- \sum_{i=1}^6 \frac{4(4-3)}{2}$

$Z = 28 - 12- 6 \cdot 2$

Z = 4

Längen von Diagonalen

• Die Länge der Raumdiagonale eines Quaders (Seitenlängen a, b, c) beträgt $d = \sqrt{a^2+b^2+c^2}$.

• Für den Spezialfall des Würfels ergibt sich daraus $d = a\sqrt{3}$.