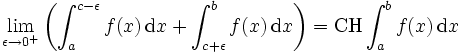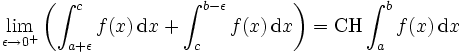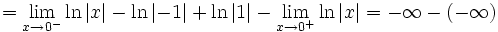- Cauchy'scher Hauptwert
- Dieser Artikel behandelt den Hauptwert in der Integralrechnung. Für die Bedeutung des Hauptwertes bei komplexen Logarithmen, siehe Logarithmus.
- uneigentlich an
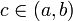 , so bezeichnet man den Grenzwert
, so bezeichnet man den Grenzwert
- uneigentlich an a und/oder b, so bezeichnet man den Grenzwert
![\Rightarrow \int_{-1}^{1} \frac{1}{x}\,\mathrm dx = \int_{-1}^{0} \frac{1}{x}\,\mathrm dx + \int_{0}^{1} \frac{1}{x}\mathrm dx = \left[ \ln\left|x\right| \right]_{x=-1}^0 + \left[ \ln\left|x\right| \right]_{x=0}^{1}](/pictures/dewiki/56/8165e390e0eca08e5a99b64c4cd73637.png)
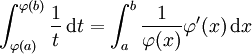
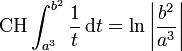
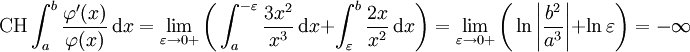
Als cauchyschen Hauptwert (nach A. L. Cauchy) bezeichnet man im mathematischen Teilgebiet der Analysis den Wert, den man einem divergenten Integral zuordnen kann, wenn sich divergente Teile verschiedenen Vorzeichens gegenseitig aufheben.
Definition
Ist das Integral 
als den Cauchyschen Hauptwert. Es ist auch gebräuchlich, "V.P." (aus dem Franz.: "valeur principal") oder "P.V." (aus dem Engl.: "principal value") anstatt "CH" zu schreiben.
Beispiel (CH 1/x)
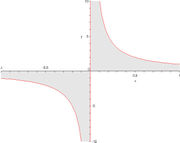
Wir betrachten das bestimmte Integral 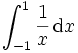 .
.
Der Integrand ist für x = 0 (ein innerer Punkt des Integrationsbereichs ( − 1,1)) nicht definiert. Damit ist dieses Integral uneigentlich an 0.
Die Stammfunktion des Integranden  ist
ist 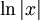 (siehe Tabelle von Ableitungs- und Stammfunktionen).
(siehe Tabelle von Ableitungs- und Stammfunktionen).
Mit dieser Methode kann dem Integral also kein eindeutiger Wert zugeordnet werden, der Cauchysche Hauptwert beträgt jedoch 0:
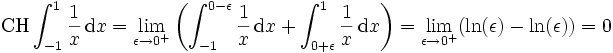
Der Cauchy-Hauptwert stellt somit eine Erweiterung des Integralbegriffs dar, da das Integral weder als Riemannintegral, noch als Lebesgue-Integral existiert.
Wenn f(x) auf der reellen Achse stetig und nur auf einem beschränkten Intervall von Null verschieden ist, existiert also insbesondere der Ausdruck 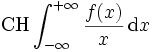 .
.
Das heißt, dass 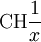 wie die Dirac-Funktion δ(x) als Verallgemeinerte Funktion (Distribution) definiert werden kann.
wie die Dirac-Funktion δ(x) als Verallgemeinerte Funktion (Distribution) definiert werden kann.
Substitution i.a. nicht erlaubt
Der Hauptwert eines Integrals bleibt jedoch im allgemeinen nicht unter Substitution invariant. Wenn man etwa die Funktion  durch
durch 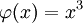 für
für 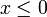 und
und 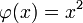 für
für 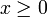 definiert, so gilt zwar nach der Substitutionsregel
definiert, so gilt zwar nach der Substitutionsregel
wann immer 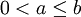 oder
oder 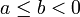 gilt. Für a < 0 < b ist jedoch der Hauptwert des einen Integrals eine endliche Zahl, der Hauptwert des zweiten Integrals ist aber
gilt. Für a < 0 < b ist jedoch der Hauptwert des einen Integrals eine endliche Zahl, der Hauptwert des zweiten Integrals ist aber 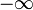 :
:
Wikimedia Foundation.