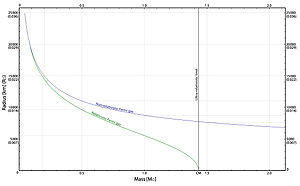
Chandrasekhar-Masse

Chandrasekhar-Grenze

Die Chandrasekhar-Grenze ist die theoretische obere Grenze für die Masse eines Weißen Zwergsterns, die von dem amerikanischen Astrophysiker und Nobelpreisträger Subrahmanyan Chandrasekhar hergeleitet wurde. Unabhängig von Chandrasekhar wurde dieselbe Obergrenze schon früher von Wilhelm Anderson (1929, Tartu) und Edmund Stoner (1930, Leeds) berechnet.

Nach dem Erlöschen seiner Kernfusionsprozesse fällt ein Stern wie die Sonne in sich zusammen und bildet einen Weißen Zwerg. Dies ist für alle Sterne möglich, deren Masse kleiner als die Chandrasekhar-Grenze ist. Andernfalls reicht der Druck der Sternmaterie nicht aus, um den Weißen Zwerg zu stabilisieren. Je nach Masse erfolgt stattdessen ein Kollaps zum Neutronenstern oder Schwarzen Loch.

Weiße Zwege werden als ein ideales entartetes Elektronengas beschrieben. Die Herleitung der Chandrasekhar-Grenze beruht daher auf der statistischen Quantenmechanik, genauer auf der Fermi-Dirac-Statistik, weil es sich bei Elektronen um Fermionen handelt. Effekte der allgemeinen Relativitätstheorie werden dabei außer Acht gelassen, da diese erst bei noch kompakteren Sternen eine Rolle spielen. Die Formel für die Grenzmasse ergibt sich zu

$M_{krit}=1.45727\left( \frac{2}{\eta} \right)^2 M_{\odot}$

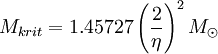
Dabei gibt η = A / Z an, wie viele Nukleonen im Mittel auf ein Elektron kommen, wenn man annimmt, dass weiße Zwerge elektrisch neutral sind. Die Sternmaterie ist dabei aus Atomen mit A Nukleonen und Z Protonen aufgebaut.

Beispiele

Für weiße Zwerge, die im Wesentlichen aus dem Kohlenstoff-Isotop 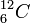${}^{12}_6 C$ oder dem Sauerstoff-Isotop 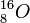${}^{16}_8 O$ bestehen, ist

η = 12 / 6 = 16 / 8 = 2.

Daraus ergibt sich direkt die erwähnte kritische Masse von 1,457 Sonnenmassen. Ein Beispiel für einen solchen Stern ist Sirius B. Für weiße Zwerge mit einem Eisenkern aus 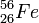${}^{56}_{26} Fe$ ist hingegen

$\eta = 56/26 \approx 2,154$.

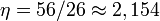Ihre Grenzmasse liegt demnach bei 1,256 Sonnenmassen. Die Chandrasekhar-Grenze ist daher nicht so zu verstehen, dass sie von jedem Stern erreicht werden kann. Es hängt von der Art der Sternmaterie ab, welche Obergrenze jeweils vorliegt.

Neutronensterne und Quarksterne

Für Neutronensterne gibt es eine äquivalente Grenze, die Tolman-Oppenheimer-Volkoff-Grenze. Ebenso wird für die hypothetischen Quarksterne eine entsprechende Grenze angenommen, doch sind die Zustandsgleichungen dieser exotischen Arten der entarteten Materie bislang nicht genau bekannt.

Weblinks

• On Stars, Their Evolution and Their Stability, Nobel Prize lecture, Subrahmanyan Chandrasekhar, December 8, 1983.
• White dwarf stars and the Chandrasekhar limit, Masters' thesis, Dave Gentile, DePaul University, 1995.
• Estimating Stellar Parameters from Energy Equipartition, sciencebits.com. Discusses how to find mass-radius relations and mass limits for white dwarfs using simple energy arguments.