- Linkwitz-Riley-Filter
-
Ein Linkwitz-Riley-Filter (L-R-Filter) ist ein elektronischer Filter, welcher in Linkwitz-Riley-Frequenzweichen benutzt wird. Es ist nach seinen Erfindern Siegfried Linkwitz und Russ Riley benannt.[1] Es ist auch als Doppeltes Butterworth-Filter bekannt, da er durch Kaskadierung zweier Butterworth-Filter gebildet wird.
Inhaltsverzeichnis
Allgemeines
Vergleich der Amplituden von Butterworth- und Linkwitz-Riley-Filtern in Frequenzweichen. Butterworth-Frequenzweichen haben eine +3dB-Spitze bei der Bemessungsfrequenz, der bei Linkwitz-Riley-Filtern nicht auftritt.
Eine L-R-Frequenzweiche besteht aus einer Parallelanordnung je eines L-R-Tiefpasses und eines L-R-Hochpasses, deren Ausgänge z.B. zur Ansteuerung von Leistungsendstufen zum Betrieb von Mehrwege-Aktiv-Lautsprechersystemen benutzt werden können. Die Bemessungsfrequenz beider Filter ist gleich und wird bei Frequenzweichen-Anordnung Übernahme-Frequenz genannt.
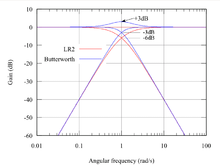
L-R-Filter werden durch Kaskadierung zweier Butterworth-Filter realisiert, die jeweils eine Verstärkung von −3 dB an ihrer Bemessungsfrequenz aufweisen. Das entstandene Linkwitz-Riley-Filter besitzt nun eine Verstärkung von −6 dB Bei der Bemessungsfrequenz.
Bei Summierung des Hochpass- und des Tiefpass-Ausgangs ist die Verstärkung bei der Übernahmefrequenz 0 dB, die ganze Anordnung verhält sich wie ein Allpass mit flachem Amplitudengang und sich über die Frequenz langsam ändernder Phase. Der flache Amplitudengang ist im Vergleich zu Butterworth-Frequenzweichen der größte Vorteil, weil diese bei Summation der Ausgänge eine Verstärkung von +3 dB bei der Übernahme-Frequenz haben.
Kaskadierung zweier Butterworth-Filter n-ter Ordnung ergeben ein Linkwitz-Riley-Filter 2n-ter Ordnung. Theoretisch kann auf diese Weise jede L-R-Frequenzweiche 2n-ter Ordnung gebaut werden. Frequenzweichen mit höherer als 4. Ordnung werden kaum genutzt, da die Gruppenlaufzeit um die Übernahmefrequenz herum zu stark zunimmt. Darüber hinaus steigt bei größeren Ordnungen als 4 die Komplexität der elektrischen Aufbaus zu stark. Das Mehr an Bauteilen macht das System fehler- und störanfällig und zu stark abhängig von Toleranzen der einzelnen Bauteile.
Oft genutzte Typen
Zweite Ordnung (LR2, LR-2)
Linkwitz-Riley-Frequenzweichen Zweiter Ordnung haben eine Steilheit von 12 dB/Oktave (40 dB/Dekade). Man kann sie aus zwei Passiven Filtern erster Ordnung bauen oder nach Sallen-Key-Topologie mit einer Güte von Q0=0.5. Die Phasendifferenz von 180° zwischen Tiefpass- und Hochpass-Ausgang der Weiche kann durch invertieren eines Signals ausgeglichen werden. In Lautsprechern wird dies durch umpolen eines Chassis erreicht, wenn man passive Frequenzweichen einsetzt. Bei aktiven Frequenzweichen fügt man einen als invertierenden Einheitsverstärker beschalteten Operationsverstärker (OPV) hinzu oder lässt einen OPV das Signal invertieren. Bei symmetrischer Verkabelung können hierzu beide Signaladern (der "kalte" mit dem "heißen" Leiter) vertauscht werden.
Vierte Ordnung (LR4, LR-4)
Linkwitz-Riley-Frequenzweichen Vierter Ordnung sind die meistgenutzten Lautsprecher-Frequenzweichen. Zwei Butterworth-Filter werden dazu kaskadiert. Die Steilheit beträgt 24 dB/Oktave (80 dB/Dekade). Die Phasendifferenz zwischen Tiefpass- und Hochpass-Ausgang der Weiche ist 360°, so scheinen sie in Phase zu sein, wobei der Tiefpass eine volle Periode nacheilt.
Achte Ordnung (LR8, LR-8)
Linkwitz-Riley-Frequenzweichen Achter Ordnung sind mit 48 dB/Oktave (160 dB/Dekade) sehr steil. Man baut sie aus zwei kaskadierten Butterworth-Filter 4. Ordnung.
Weblinks
- Linkwitz Lab: Crossovers
- Linkwitz Lab: Active Filters
- Linkwitz-Riley Crossovers: A Primer
- Glossary: Linkwitz-Riley
Einzelnachweise
Wikimedia Foundation.
