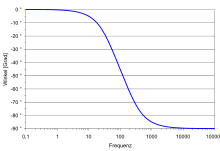
Phasengang

Der Phasengang, der auch Phasenfrequenzgang oder Phasenmaß heißt, englisch: phase response, wird meistens im Zusammenhang mit dem Amplitudengang oder Amplitudenfrequenzgang betrachtet.

Beispiel eines Phasengangs eines Tiefpasses

Aus der Phasenverschiebung lässt sich über eine Ableitung nach der Frequenz die Gruppenlaufzeit errechnen, die anschaulich gesprochen die frequenzabhängige Signalverzögerung beschreibt.

Amplituden- und Phasengang, zeigen in der Darstellung der Frequenzebene in einem Signal oder frequenzsensitiven System die Abhängigkeit der Amplitude und der Phase von der Frequenz (Amplituden- und Phasendiagramm).

Beide Größen als Graph dargestellt bezeichnet man auch als Amplitudengang (Betragsfrequenzgang) bzw. Phasengang (Phasenfrequenzgang), in Kombination auch Bode-Diagramm genannt. Werden beide Informationen zu einer komplexen Funktion zusammengefasst, spricht man auch vom komplexen Frequenzgang.

Messtechnische Einschränkungen

In der Messtechnik wird zum Aufnehmen des Phasengang üblicherweise ein kontinuierliches Sinussignal verwendet, was dazu führt, dass Phasenverschiebungen nur im Bereich von ±180° bzw. ±π gemessen werden können. Aus einem messtechnisch aufgenommenen Phasengang lässt sich daher nur bedingt die Gruppenlaufzeit ableiten.

Theorie

Zunächst trennt man die Übertragungsfunktion eines kausalen, linearen, zeitinvarianten Systems nach Real- und Imaginärteil auf:

$\mathcal {}H(\mathrm{j}\omega)=M(\omega)+\mathrm{j}N(\omega)$

In einem zweiten Schritt benötigt man das Übertragungsmaß

$\mathcal {}\Gamma(\omega) = A(\omega)+\mathrm{j}B(\omega)$,

das mit der Übertragungsfunktion durch folgende Gleichung zusammenhängt:

$H(j\omega) = e^{-\Gamma} = e^{-(A(\omega)+\mathrm{j}B(\omega))} = e^{-A(\omega)}\cdot e^{-\mathrm{j}B(\omega)}$

Der zweite Faktor, $\mathcal {}e^{-jB(\omega)}$, ist hierbei der Phasenterm, dementsprechend ist das $\mathcal {}B(\omega)$ die Phase in Abhängigkeit von der Frequenz und stellt den Phasengang dar.

Führt man nun die Phase $\mathcal {}B(\omega)$ auf die ursprüngliche Übertragungsfunktion zurück, ergibt sich

$B(\omega) = -\arctan{\frac{N(\omega)}{M(\omega)}}$

Die Nicht-Eindeutigkeit der Arkustangens-Funktion führt zu den in den oberen Abschnitten beschriebenen Einschränkungen (Wertebereich nur $\mathcal {}-\pi$ bis $\mathcal {}\pi$).

Problematisch sind diejenigen Stellen, an denen die Übertragungsfunktion $\mathcal {}H(j\omega)$ Null- oder Polstellen aufweist, da sich durch

$\mathcal {}\Gamma = - ln{H(\mathrm{j}\omega)}$

für $\mathcal {}\Gamma$ dort dann Singularitäten ergeben.

Um die Phase nun bestimmen zu können, ist es sinnvoll, vom Fourier-Bereich in den Laplace-Bereich (s-Ebene) zu wechseln (vgl. Laplace-Transformation), also nicht nur die imaginäre Achse, sondern die komplette komplexe Frequenzebene zu betrachten. Eine erste Forderung, die benötigt wird, um den Phasenverlauf bestimmen zu können ist

$\mathcal {}\Gamma(0) = 0$

Damit ist ein Startwert festgelegt, um die Nicht-Eindeutigkeit der Phase ($\mathcal {}\pm 2\pi$) zu umgehen. Um den Phasenverlauf nun tatsächlich bestimmen zu können, läuft man in der s-Ebene entlang der imaginären Achse ausgehend vom Ursprung zu den positiven Frequenzen und vom Ursprung aus in Richtung der negativen Frequenzen und umgeht dabei die Pol- und Nullstellen durch halbkreisförmige „Einbuchtungen“ in die rechte Halbebene.

Erklärung anhand eines Beispiels: n-fache Nullstelle von $\mathcal {}H(s)$ bei $\mathcal {}s = \mathrm{j}\omega_0$.

Taylor-Entwicklung in der Nähe der Nullstelle, Abbruch nach dem ersten Glied:

$\mathcal {}H(s) = (s-\mathrm{j}\omega_0)^n H^{(n)}$

wobei $\mathcal {}H^{(n)}$ den Wert der n-ten Ableitung an der Stelle $\mathcal {}\mathrm{j}\omega_0$ meint.

Halbkreisförmige Einbuchtung: Radius $\mathcal {}\rho$, Winkel $\mathcal {}\theta = [-\tfrac{\pi}{2} \ldots \tfrac{\pi}{2}]$

$\mathcal {}s = \mathrm{j}\omega_0+\rho e^{\mathrm{j}\theta}$

folgt:

$\mathcal {}H(s)(s-\mathrm{j}\omega_0)^n H^{(n)} = (\mathrm{j}\omega_0+\rho e^{\mathrm{j}\theta}-\mathrm{j}\omega_0)^n H^{(n)} = \rho^nH^{(n)}e^{\mathrm{j}n\theta}$

und demnach:

$\mathcal {}\Gamma(\omega) = -\ln{H(s)}=-\ln(\rho^nH^{(n)}e^{\mathrm{j}n\theta})=-n\ln{\rho}-\ln {H^{(n)}}-\mathrm{j}n\theta$

für die Phase gilt nun:

$\mathcal {}B(\omega) = \arg(H^{(n)})-n\theta$

Da sich $\mathcal {}\theta$ entlang dieser Einbuchtung um $\mathcal {}\pi$ ändert, ändert sich die Phase insgesamt um $\mathcal {}-n\cdot \pi$.

Bei einer Polstelle ergeben sich die umgekehrten Vorzeichenverhältnisse, die Phase nimmt um $\mathcal {}n\cdot \pi$ zu.

Literatur

• Alfred Fettweis: Elemente nachrichtentechnischer Systeme. 2. Auflage. J.Schlembach Fachverlag, Wilburgstetten 2004, ISBN 3-935340-41-9.
• Gert Hagmann: Grundlagen der Elektrotechnik. 6. Auflage. AULA-Verlag GmbH, Wiesbaden 1997, ISBN 3-89104-614-6.
• Curt Rint: Handbuch für Hochfrequenz- und Elektro- Techniker Band 2. 13. Auflage. Hüthig und Pflaum Verlag GmbH, Heidelberg 1981, ISBN 3-7785-0699-4.

Siehe auch

• Frequenzgang (System) | Ortskurve (Systemtheorie) | Bode-Diagramm | Smith-Diagramm

Weblinks

• Es gibt Tonmeister, die vom Phasengang falsch erwarten, dass er so konstant verläuft wie der Amplitudenfrequenzgang - pdf (547 kB)