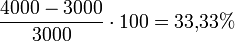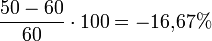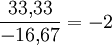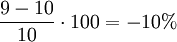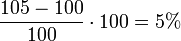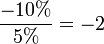Absatzelastizität

Die Preiselastizität ist ein Maß dafür, welche relative Änderung sich bei der Angebots bzw. Nachfragemenge ergibt, wenn eine relative Preisänderung eintritt. ^[1] Je höher die Preiselastizität ist, desto stärker reagiert die Menge auf den geänderten Preis. Die Preiselastizität eines Gesamtmarktes tendiert dazu, geringer als die Elastizität eines einzelnen Gutes zu sein, das bei einer Preisänderung gegen ein anderes ausgetauscht (substituiert) werden kann.

Eine besondere Form der Preiselastizität ist die Kreuzpreiselastizität, bei der dargestellt wird, wie sich die Preisänderung eines Gutes auf die Mengenänderung eines anderen Gutes auswirkt.

Grundsätzlich lässt sich bei den Elastizitäten die Beeinflussung der Nachfrage- und der Angebotsmenge unterscheiden, weshalb man in der Gesamtheit vier Elastizitäten genauer benennt. Wird die Preiselastizität ohne nähere Präzisierung genannt, ist in der Regel die Preiselastizität der Nachfrage gemeint.

• Preiselastizität der Nachfrage
• Preiselastizität des Angebots
• Kreuz-Preiselastizität der Nachfrage
• Kreuz-Preiselastizität des Angebots

Weiterhin unterscheidet man zwischen einer kurzfristigen und langfristigen Elastizität. Da es z. B. durch technischen Fortschritt möglich ist, sich an bestimmte Preisänderungen anzupassen, ist die langfristige Preiselastizität häufig geringer als die kurzfristige Preiselastizität.

Definition

Die Preiselastizität ist definiert als relative Mengenänderung (der am Markt zu diesem Preis angebotenen Güter) dividiert durch relative Preisänderung. Es werden hier verschiedene Herangehensweisen unterschieden.

Bogenelastizität

mit dem Preis P und der Menge Q, wobei P₁ der alte Preis und P₂ der neue bedeuten, Q analog,

$\eta_{Q,P} = \frac{\frac{(Q_{2}-Q_{1})}{Q_{1}}}{\frac{(P_{2}-P_{1})}{P_{1}}}$.

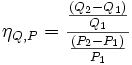Man könnte diese Elastizität als ungefähre durchschnittliche relative Änderung von Q interpretieren.

Mittelwertmethode

Sie ist eine Variante der Bogenelastizität, bei der die Änderungen nicht auf einen festen Wert Q oder P bezogen werden, sondern auf das Mittel von P₁ und P₂, Q analog. Man erhält dann

$\eta_{Q,P} = \frac{\frac{Q_{2}-Q_{1}}{(Q_{2}+Q_{1})/2}}{\frac{P_{2}-P_{1}}{(P_{2}+P_{1})/2}}$.

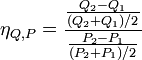Elastizitätsfunktion

Es wird hier eine infinitesimale (unendlich kleine) Änderung des Preises p bezüglich einer Preis-Absatz-Funktion p(q) betrachtet. Für die Bereiche, in denen p(x) und η_x,p definiert sind und in denen p(q) differenzierbar ist, ergibt sich die Elastizitätsfunktion

$\eta_{x,p} = \frac{\frac{\delta x}{x}}{\frac{\delta p}{p}} = \frac{\delta x}{\delta p}\cdot\frac{p}{x}$.

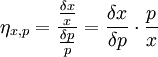Kategorisierung

Im folgenden sollen die möglichen Elastizitäten dargestellt werden. Die Beispiel behandeln, sofern nicht anders beschrieben, stehts die Auswirkungen einer Preissenkung auf die Nachfragemenge. Daraus ergibt sich, bis auf die anormale Elastizität, stehts ein negatives Vorzeichen der Elastizität.

quantitiv

also: in welchem Umfang beeinflusst der Preis die Mengenänderung bei Angebot und Nachfrage

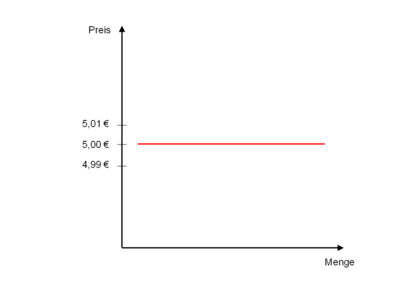
vollkommen elastisch (perfectly elastic demand)
Darstellung	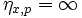$\eta_{x,p} = \infty$
Erklärung	Eine minimal (infinitesimale) Preisänderung bewirkt eine unendliche Mengenänderung. Die vollkommene Elastizität ist nur modellhaft zu betrachten, sie wird in der realen Wirtschaft nicht anzutreffen sein.
Beispiel	Eine 5-Euro Banknote würde zu einem Preis von 5,01 Euro keine Nachfrager finden. Kostet die Banknote hingegen genau 5,00 Euro, ist die nachgefragte Menge beliebig groß. Die Nachfrage kaufen die Banknote tatsächlich nur dann, wenn sie benötigt wird. Bei einem Preis von 4,99 Euro ist sie sogar unendlich groß, da jetzt jeder Nachfrage versuchen wird, diese Banknote zu erstehen.
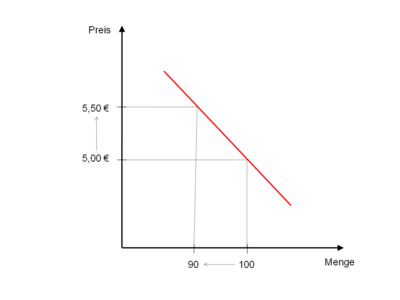
sehr elastisch (elastic demand)
Darstellung	ηx,p > 1
Erklärung	Eine Preisänderung bewirkt eine überproportionale Mengenänderung.
Beispiel	Eine starke Reaktion der Nachfrage auf Preisveränderungen zeigt sich beispielsweise bei guten Substituten, wie Nägel einer bestimmten Sorte. Wird der Preis erhöht, wechseln möglicherweise fast alle Kunden zur Konkurrenz, wird der Preis verringert, wechseln die Kunden wieder zurück.
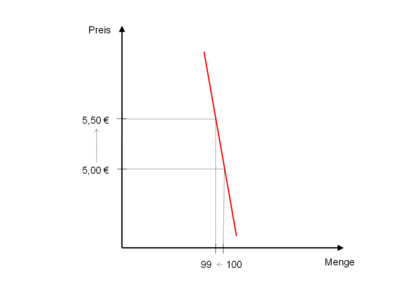
proportional elastisch (unit elastic demand)
Darstellung	ηx,p = 1
Erklärung	Eine 1%ige Preisänderung bewirkt eine 1%ige Mengenänderung.
Beispiel	Der Fall der Einheitselastizität ist nicht zu verwechseln mit dem der iso-elasticity: Im ersten Fall ist die Elastizität an einem Punkt der Nachfrage gleich eins. Im zweiten Fall ist die Preiselastizität der Nachfrage konstant, d.h. für jeden Preis gleich groß.
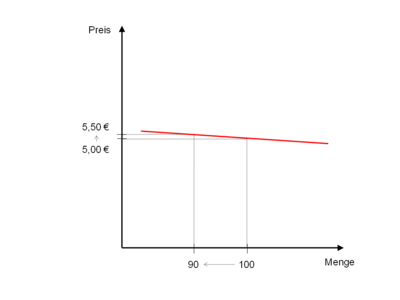
unelastisch (inelastic demand)
Darstellung	ηx,p < 1
Erklärung	Eine Preisänderung bewirkt eine unterproportionale Mengenänderung.
Beispiel	Eine schwache Reaktion der Nachfrage auf Preisveränderungen, zeigt sich besonders bei lebensnotwendigen Wirtschaftsgütern wie Nahrungsmittel, die schlecht substituiert werden können. Weitere Gründe sind die mangelnde Wahrnehmung der Preisänderung und die Aufwendigkeit der Suche nach Substituten.
vollkommen unelastisch (perfectly inelastic demand)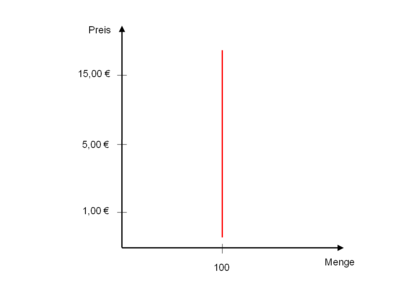
Darstellung	ηx,p = 0
Erklärung	Eine maximale Preisänderung bewirkt keine Mengenänderung.
Beispiel	Es tritt keine Reaktion der Nachfrage auf Preisveränderungen ein. Dies zeigt sich beispielsweise bei lebenswichtigen Medikamenten, da trotz Preiserhöhungen immer die gleiche Menge gekauft wird. In der Praxis findet dieser Fall seine Grenzen allerdings dort, wo sämtliche finanziellen Mittel ausgeschöpft sind.
anormal elastisch
Darstellung	ηx,p > 0
Erklärung	Die Nachfrage ist bei diesem Sonderfall positiv elastisch; ein höherer Preis induziert eine höhere Nachfrage. Die Preiselastizität der Nachfrage eines bestimmten Gutes kann allerdings nicht für jedes Preisniveau positiv sein; dies würde das Vorhandensein unendlicher finanzieller Mittel bei den Nachfragern erfordern.
Beispiel	Dies ist beispielsweise der Fall, wenn mit steigendem Preis eine zunehmende Exklusivität des Gutes assoziiert wird (Snobeffekt, demonstrativer Konsum) oder wenn aus der Erhöhung des Preises auf eine bevorstehende Verknappung des Gutes geschlossen wird (Hamsterkauf). Der Preis kann auch als Qualitätsindikator angesehen werden, oder es liegt ein Giffen-Gut (absolut inferiores Gut) vor.

kompetitiv (Triffinischer Koeffizient)

Die Verwendung der Kreuzpreiselastizität als Indikator der Stärke konkurrierender Unternehmen geht auf Robert Triffin zurück. Nach der Berechnung der Kreuzpreiselastizität der Nachfrage, im folgenden Triffinischer Koeffizient e, unterscheidet man drei Formen der Konkurrenz: ^[2]

e = 0	Keine Konkurrenz liegt vor, wenn die Kreuzpreiselastizität gleich Null ist. Die Änderung des Preises von Anbieter A wirkt sich nicht auf die Absatzmenge von Anbieter B aus.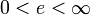
$0 < e < \infty$	Je kleiner e, desto geringer ist die Konkurrenz. Hebt Anbieter A den Preis für Milch um 100% an und steigt daraufhin die Absatzmenge der Milch von Hersteller B nur um 0,1%, ist e = 0,001 und deutet somit auf eine heterogene Konkurrenz hin.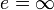
$e = \infty$	Je weiter sich e unendlich nähert, desto größer ist die Konkurrenz. Eine geringe Preisänderung eines Gutes hat bereits einen drastischen Absatzschub eines anderen Gutes zur Folge, es handelt sich um homogene Konkurrenz. e = unendlich -> homogene Konkurrenz: senkt Hersteller A den Preis seiner Milch infinitesimal, sinkt die Absatzmenge der Milch von Hersteller B drastisch

Anwendung

Beim Wettbewerb um die genaueste Einschätzung des Kundenverhaltens im Marketing hilft die Beobachtung der Preiselastizität der Nachfrage bei der Gestaltung einer strategischen Preispolitik. Im Gegensatz zu operativen Preismaßnahmen, die beispielsweise dem kurzzeitigen Abverkauf von Saisonware oder der Führung von Wettbewerbsaktionen dienen, hat die Kenntnis der Preiselastizität der Nachfrage im Markt eine strategische Bedeutung. Es wird unter anderem erfasst, ab welchem Marktpreis eine Erhöhung der Preise die abgesetzte Menge so stark senkt, dass der Gesamtumsatz geringer ist als vor der Preiserhöhung. Auch für den Fall, dass der Absatz eines Produktes oder einer Dienstleistung hinter den Erwartungen zurückbleibt, kann man mit Hilfe der Elastizität bestimmen, ob eine Preissenkung sinnvoll ist.

Die Preiselastizität kann als Kennzahl auch für das Controlling im Unternehmen angewendet werden, um die Stabilität der eigenen Preise bei Nachfrageschwankungen zu erfassen.

Im volkswirtschaftlichen Rahmen dient die Preiselastizität zu Berechnung von Steueraufkommen. Je höher die Elastizität, desto eher wird das besteuerte Gut nach einer Steuererhöhung nicht mehr konsumiert werden. Die Steuer hat deshalb eine Lenkung des Konsumverhaltens zum Ziel (siehe auch Lenkungssteuer). Ist die Elastizität hingegen gering, hat die Steuer den Charakter einer Aufkommenssteuer.

Beispiele

Preissenkung

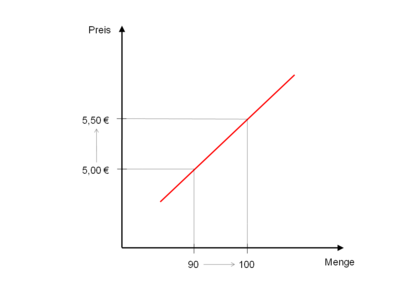
Ein Unternehmen verändert seinen Preis von derzeit 60 auf 50 Euro. Dies hat zur Folge, dass die Absatzmenge von derzeit 3.000 auf 4.000 Stück steigt.

Prozentuale Absatzsteigerung

• $\frac{4000 - 3000}{3000} \cdot 100 = 33{,}33 %$

Prozentuale Preissenkung

• $\frac{50 - 60}{60} \cdot 100 = -16{,}67 %$

Preiselastizität

• $\frac{33{,}33}{-16{,}67} = -2$

Die Nachfrage ist somit elastisch.

Preissteigerung

Ein Händler erhöht den Preis eines Marken-Sakkos von derzeit 100 auf 105 €. Dies hat zur Folge, dass die Nachfrage von derzeit 10 auf 9 Stück sinkt.

Prozentualer Absatzrückgang

• $\frac{9 - 10}{10} \cdot 100 = -10%$

Prozentuale Preiserhöhung

• $\frac{105 - 100}{100} \cdot 100 = 5%$

Preiselastizität

• $\frac{-10%}{5%} = -2$

Die Nachfrage ist somit elastisch.

Weiteres Beispiel

Zwischen einer Menge m und dem Marktpreis p besteht ein Zusammenhang, der durch folgende Funktion wiedergegeben wird:

m = 24 - 6p

Frage: Wie hoch ist der Elastizitätskoeffizient bei p = 3 ?

Lösung

Hier sind keine prozentualen Veränderungen vorhanden, die dividiert werden können. Es wird sodann mit der eingangs genannten Elastizitätsformel gerechnet. Zu beachten ist, dass der Teil „Delta (Wirkung) / Delta (Ursache)“ der Formel) gleich der Ableitung der folgenden gegebenen Funktion ist. Es bleibt sodann nur der Koeffizient von p übrig (hier −6) und dieser kann in die Elastzititätsformel eingesetzt werden.

Vorgehen

1)

• m = 24 - 6*p = ?

• m = 24 - 6*3 = 6 für p = 3

2) Ableiten von "24-6p" => = f'(m) = -6

3) Formel ist nun E = f'(m) * p/m

4) Einsetzen: (−6) * 3/6 = (−3) = E = > 1 (weil absoluter Betrag von −3 genommen wird)

E = > 1 bedeutet eine elastische Beziehung zwischen p und m. Würde eine Kreuzpreiselastizität (mit m1 und p2) dargestellt, so ließe das Vorzeichen auf substitutive (+) oder komplementäre (-) Güter schließen, im Falle der Einkommenselastizität auf superiore(+) bzw. inferiore(-) Güter. Eine E = 0 oder nahe 0 hingegen gälte für Zwangsgüter wie Lebensmittel, Drogen oder Kraftstoffe u. Ä. (vollkommen unelastisch).

Siehe auch

• Elastizität (Wirtschaft)
• Einkommenselastizität
• Amoroso-Robinson-Relation

Weblinks

• Kurvendiskussion mit Animation

Einzelnachweise

1. ↑ Gerhard Graf: Grundlagen der Volkswirtschaftslehre, Physica-Verlag, 2. Aufl., 2002, S. 41
2. ↑ vgl. Aus Wöhe: Triffin, R., Monopolistic Competition and General Equilibrium Theory, Cambridge (Mass). 1949, S. 97ff.