Hierarchische Clusteranalyse

Als Hierarchische Clusteranalyse bezeichnet man eine bestimmte Familie von distanzbasierten Verfahren zur Clusteranalyse (Strukturentdeckung in Datenbeständen). Cluster bestehen hierbei aus Objekten, die zueinander eine geringere Distanz (oder umgekehrt: höhere Ähnlichkeit) aufweisen als zu den Objekten anderer Cluster. Man kann die Verfahren in dieser Familie nach den verwendeten Distanz- bzw. Proximitätsmaßen (zwischen Objekten, aber auch zwischen ganzen Clustern) und nach ihrer Berechnungsvorschrift unterscheiden.

Untergliedert man nach der Berechnungsvorschrift, so unterscheidet man zwei wichtige Typen von Verfahren:

• die divisiven Clusterverfahren, in denen zunächst alle Objekte als zu einem Cluster gehörig betrachtet und dann schrittweise die bereits gebildeten Cluster in immer kleinere Cluster aufgeteilt werden, bis jeder Cluster nur noch aus einem Objekt besteht. (Auch bezeichnet als „Top-down-Verfahren“)

• die agglomerativen Clusterverfahren, in denen zunächst jedes Objekt einen Cluster bildet und dann schrittweise die bereits gebildeten Cluster zu immer größeren zusammengefasst werden, bis alle Objekte zu einem Cluster gehören. (Auch bezeichnet als „Bottom-up-Verfahren“)

Für beide Verfahren gilt, dass einmal gebildete Cluster nicht mehr verändert werden können. Die Struktur wird entweder stets nur verfeinert („divisiv“) oder nur vergröbert („agglomerativ“), so dass eine strikte Cluster-Hierarchie entsteht. An der entstandenen Hierarchie kann man nicht mehr erkennen, wie sie berechnet wurde.

Eine agglomerative Berechnung kommt in der Praxis und Forschung sehr viel häufiger vor, da sie im Allgemeinen eine einfachere Berechnung ermöglicht: Agglomerativ gibt es in jedem Schritt O(n²) Möglichkeiten, Cluster zusammenzufassen, was zu einer naiven Gesamtkomplexität von O(n³) führt. In speziellen Fällen sind auch Verfahren mit einer Gesamtkomplexität von O(n²) bekannt. Divisiv gibt es aber naiv in jedem Schritt O(2ⁿ) Möglichkeiten, den Datensatz zu teilen.

Vorteile und Nachteile

Die Vorteile der hierarchischen Clusteranalyse sind die Flexibilität durch Verwendung komplexer Distanzmaße, dass das Verfahren außer der Distanzfunktion keine eigenen Parameter hat und dass das Ergebnis eine Cluster-Hierarchie ist, die auch Unterstrukturen erlaubt.

Die großen Nachteile der hierarchischen Clusteranalyse sind die Laufzeit-Komplexität und der Analyseaufwand des Ergebnisses. Andere Verfahren, wie z.B. der k-Means-Algorithmus, DBSCAN oder der ebenfalls hierarchische OPTICS-Algorithmus, liefern eine einzelne Partitionierung der Daten in Cluster. Die hierarchische Clusteranalyse liefert zahlreiche solcher Partitionierungen, und der Anwender muss sich entscheiden, auf welcher Höhe des Dendrogramms er partitioniert. Gibt es hierarchische Cluster mit unterschiedlicher Dichte, so kann es notwendig sein, auf unterschiedlichen Höhen zu partitionieren: während ein Cluster auf einer Höhe noch mit seinen Nachbarn verbunden ist, zerfällt ein anderer ("dünnerer") Cluster auf dieser Höhe schon in einzelne Objekte.

Als weiterer Nachteil der hierarchischen Clusteranalyse gilt, dass sie keine Clustermodelle liefert. So entstehen beispielsweise je nach verwendeten Maßen Ketteneffekte ("single-link effekt") und es werden aus Ausreißern oft winzige Cluster erzeugt, die nur aus wenigen Elementen bestehen. Die gefundenen Cluster müssen daher meist nachträglich analysiert werden, um Modelle zu erhalten.

Visualisierung als Dendrogramm

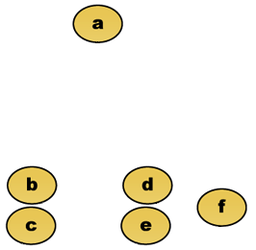
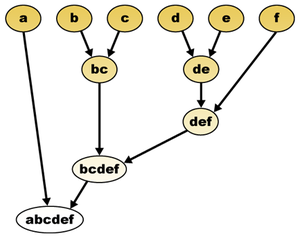
Zur Visualisierung der bei einer hierarchischen Clusterung entstehenden Baumstruktur kann das Dendrogramm (griech. δένδρον (dendron) = Baum) genutzt werden. Das Dendrogramm ist ein Baum, der die hierarchische Zerlegung der Datenmenge O in immer kleinere Teilmengen darstellt. Die Wurzel repräsentiert ein einziges Cluster, das die gesamte Menge O enthält. Die Blätter des Baumes repräsentieren Cluster, in denen sich je ein einzelnes Objekt der Datenmenge befindet. Ein innerer Knoten repräsentiert die Vereinigung aller seiner Kindknoten. Jede Kante zwischen einem Knoten und einem seiner Kindknoten hat als Attribut noch die Distanz zwischen den beiden repräsentierenden Mengen von Objekten.

• Datensatz und Dendrogramm
• 

  Datensatz. Die Objekte b und c sowie d und e liegen sehr dicht zusammen.

• 

  Dendrogramm für single-linkage. b und c sowie d und e werden als erstes zusammengefasst.

Agglomerative Berechnung

Die agglomerative Berechnung einer hierarchischen Clusteranalyse ist der einfachste und flexibelste Fall. Hierbei können beliebige Distanzmaße mit polynomial vielen Distanzberechnungen verwendet werden.

Beschreibung

Beim Anhäufen der Cluster wird zunächst jedes Objekt als ein eigener Cluster mit einem Objekt aufgefasst. Nun werden in jedem Schritt die jeweils einander nächsten Cluster zu einem Cluster zusammengefasst. Das Verfahren kann beendet werden, wenn alle Cluster eine bestimmte Distanz/Ähnlichkeit zueinander überschreiten/unterschreiten oder wenn eine genügend kleine Zahl von Clustern ermittelt worden ist. Dies ist bei Clustern mit nur einem Objekt, wie sie zu Anfang vorgegeben sind, trivial. Sobald ein Cluster aus mehreren Objekten besteht, muss jedoch entschieden werden, welches Objekt aus dem Cluster zur Proximitätsmessung mit dem nächsten Objekt/Cluster verwendet wird. Hier gibt es unterschiedliche Möglichkeiten, in denen sich die einzelnen agglomerativen Verfahren unterscheiden.

Für die Durchführung einer agglomerativen Clusteranalyse müssen

• ein Fusionierungsalgorithmus zur Zusammenfassung von Clustern ausgewählt werden und
• ein Proximitätsmaß zur Abstandsbestimmung.

Dabei ist die Wahl des Fusionierungsalgorithmus oft wichtiger als die des Proximitätsmaßes.

Beispiel

Besonders deutlich wird dies im zweiten Schritt des Algorithmus. Bei der Verwendung eines bestimmten Distanzmaßes wurden im ersten Schritt die beiden einander nächsten Objekte zu einem Cluster fusioniert. Dies kann wie folgt als Distanzmatrix dargestellt werden:

Distanz zw.	Cluster1 Objekt1	Cluster2 Objekt2	Cluster3 Objekt3	Cluster4 Objekt4
Objekt1	0
Objekt2	4	0
Objekt3	7	5	0
Objekt4	8	10	9	0

Die kleinste Distanz findet sich zwischen dem Objekt1 und Objekt2 (rot in der Distanzmatrix) und man würde daher Objekt1 und Objekt2 zu einem Cluster zusammenfassen (fusionieren). Nun muss die Matrix neu erstellt werden ("o." steht für oder), das heißt die Distanz zwischen dem neuen Cluster und Objekt3 bzw. Objekt4 muss neu berechnet werden (gelb in der Distanzmatrix):

Distanz zw.	Cluster1 Objekt1&2	Cluster2 Objekt3	Cluster3 Objekt4
Objekt1&2	0
Objekt3	7 o. 5	0
Objekt4	8 o. 10	9	0

Welcher der beiden Werte für die Distanzbestimmung relevant ist, bestimmt das Verfahren:

Verfahren	Distanz zw.	Cluster1 Objekt1&2	Cluster2 Objekt3	Cluster3 Objekt4
Single Linkage Das Single Linkage Verfahren würde den kleinsten/kleineren Wert aus dem Cluster zur Bestimmung der neuen Abstände zu den anderen Objekten verwenden, also min(5,7) = 5 und min(8,10) = 8. Dieses Verfahren neigt zur Kettenbildung.	Objekt1&2	0
	Objekt3	5	0
	Objekt4	8	9	0
Complete Linkage Das Complete Linkage Verfahren würde den größten Wert aus dem Cluster zur Bestimmung der neuen Abstände zu den anderen Objekten verwenden, also max(5,7) = 7 und max(8,10) = 10. Dieses Verfahren neigt zur bildung kleiner Gruppen.	Objekt1&2	0
	Objekt3	7	0
	Objekt4	10	9	0
Average Linkage Das Average Linkage verwendet einen Durchschnittswert auf Basis aller Distanzen zwischen dem neuen Cluster und dem betrachteten Cluster: $\tfrac1{2*1}(7+5)=6$ und $\tfrac1{2*1}(8+10)=9$	Objekt1&2	0
	Objekt3	6	0
	Objekt4	9	9	0
Average Group Linkage Das Average Group Linkage verwendet einen Durchschnittswert auf Basis aller Distanzen der Objekte des neuen Cluster und des betrachteten Cluster: $\tfrac13(4+5+7)=5,\bar{3}$ und $\tfrac13(4+8+10)=7,\bar{3}$	Objekt1&2	0
	Objekt3	5,3	0
	Objekt4	7,3	9	0
Centroid Verfahren Dieses Verfahren verwendet eine gewichtete Distanz zwischen den Clusterzentren und aufgrund der Formel unten ergibt sich: $\tfrac12 7+\tfrac12 5 -\tfrac14 4=5$ und $\tfrac12 8+\tfrac12 10 -\tfrac14 4=8$	Objekt1&2	0
	Objekt3	5	0
	Objekt4	8	9	0
Ward-Verfahren Die hier zu verwendende Distanzfunktion wird weiter unten beschrieben. Dieses Verfahren neigt zur Bildung von gleich großen Gruppen.	Objekt1&2	0
	Objekt3		0
	Objekt4		9	0

Fusionierungsmethoden

Der Abstand D zweier Cluster A und B kann beispielsweise über eine der folgenden Distanzfunktionen berechnet werden (d ist hierbei der Abstand von zwei einzelnen Objekten):

Single linkage
Minimaler Abstand aller Elementpaare aus den beiden Clustern $D_\mbox{single-linkage}(A,B):=\min_{a\in A, b\in B}\{d(a,b)\}$
Complete linkage
Maximaler Abstand aller Elementpaare aus den beiden Clustern $D_\mbox{complete-linkage}(A,B):=\max_{a\in A, b\in B}\{d(a,b)\}$
Average linkage
Durchschnittlicher Abstand aller Elementpaare aus den beiden Clustern $D_\mbox{average-linkage}(A,B):=\tfrac{1}{|A||B|}\sum_{a\in A, b\in B} d(a,b)$
Average group linkage
Durchschnittlicher Abstand aller Elementpaare aus der Vereinigung von A und B $D_\mbox{average-group-linkage}(A,B):=\tfrac{1}{(|A|+|B|)(|A|+|B|-1)}\sum_{x,y\in A \cup B} d(x,y)$
Centroid method
Abstand der Zentren der beiden Cluster $D_\mbox{centroid-distance}(A,B):=d(\bar a, \bar b)$ wobei $\bar a$ das Zentrum des Clusters A sei, $\bar b$ das des Clusters B.
Ward’s method
Zunahme der Varianz beim Vereinigen von A und B $D_\mbox{Ward}(A,B):=\frac{d(\bar a, \bar b)}{1/|A|+1/|B|}$ wobei $\bar a$ das Zentrum des Clusters A sei, $\bar b$ das des Clusters B.

Weitere Methoden sind Density Linkage, Uniform-Kernel, Wong’s Hybrid, EML, Flexible-Beta, McQuitty’s Similarity Analysis und Medoid. Von praktischer Relevanz ist hierbei vor allem single linkage, da es mit dem Algorithmus SLINK eine effiziente Berechnungsmethode erlaubt.

Zum Fusionieren der Cluster ist es jedoch nicht notwendig, immer wieder die Distanzen zwischen den Objekten neu zu berechnen. Stattdessen startet man wie in obigem Beispiel mit einer $n\times n$ Distanzmatrix. Steht fest, welche Cluster fusioniert werden, so müssen nur die Distanzen zwischen dem fusionierten Cluster und alle anderen Clustern neu berechnet werden. Jedoch kann die neue Distanz zwischen dem fusionierten Cluster $A \cup B$ einem anderen Cluster c aus den alten Distanzen mit Hilfe einer Formel berechnet werden:

$D(A \cup B,C)=\delta_1 d(A,C)+\delta_2 d(B,C)+ \delta_3 d(A,B) + \delta_4 |d(A,C)-d(B,C)|.$

Für die verschiedenen Methoden ergeben sich verschiedene Konstanten δ_i, die der folgenden Tabelle entnommen werden können. Dabei bedeutet | A | die Anzahl der Objekte im Cluster A.

Methode	δ1	δ2	δ3	δ4
Single linkage	1/2	1/2	0	-1/2
Complete linkage	1/2	1/2	0	1/2
Median method	1/2	1/2	-1/4	0
Average linkage	1/2	1/2	0	0
Average group linkage	$\tfrac{|A|}{|A|+|B|}$	$\tfrac{|B|}{|A|+|B|}$	0	0
Centroid method	$\tfrac{|A|}{|A|+|B|}$	$\tfrac{|B|}{|A|+|B|}$	-$\tfrac{|A||B|}{(|A|+|B|)^2}$	0
Ward's method	$\tfrac{|A|+|C|}{|A|+|B|+|C|}$	$\tfrac{|B|+|C|}{|A|+|B|+|C|}$	-$\tfrac{|C|}{|A|+|B|+|C|}$	0

Proximitätsmaß

→ Hauptartikel: Ähnlichkeitsanalyse

Je nach Skalenniveau der zugrunde liegende Variablen kommen verschieden Proximitätsmaße zum Einsatz:

• Bei nominalen und ordinalen Variablen werden Ähnlichkeitsmaße benutzt, d.h. ein Wert von Null bedeutet, dass die Objekte eine maximale Unähnlichkeit haben. Diese können in Distanzmaße umgewandelt werden.
• Bei metrischen Variablen werden Distanzmaße benutzt, d.h. ein Wert von Null bedeutet, dass die Objekte einen Abstand von Null, also maximale Ähnlichkeit haben.

Die folgende Tabelle zeigt einige Ähnlichkeits- bzw. Distanzmaße für binäre und metrische Variablen. Kategorielle Variablen mit mehr als zwei Kategorien können in mehrere binäre Variablen umgewandelt werden. Die Gower Distanz kann auch für nominal skalierte Variablen definiert werden.

Ähnlichkeitsmaß	s(i,j)	Distanzmaß	d(i,j)
Jaccard	$\frac{n_{11}}{n_{01}+n_{10}+n_{11}}$	Lr	$\left(\sum_{k=1}^p (x_{ik}-x_{jk})^r\right)^{1/r}$
Tanimoto	$\frac{n_{00}+n_{11}}{n_{00}+2(n_{01}+n_{10})+n_{11}}$	Euklidisch L2	$\sqrt{\sum_{k=1}^p (x_{ik}-x_{jk})^2}$
Simple Matching	$\frac{n_{00}+n_{11}}{p}$	Pearson	$\sqrt{\sum_{k=1}^p \frac{(x_{ik}-x_{jk})^2}{s_k^2}}$ mit sk die Standardabweichung der Variable k
Russel Rao	$\frac{n_{11}}{p}$	City-Block Manhattan L1	$\sum_{k=1}^p |x_{ik}-x_{jk}|$
Dice	$\frac{2n_{11}}{n_{01}+n_{10}+2n_{11}}$	Gower	$\sum_{k=1}^p \frac{|x_{ik}-x_{jk}|}{r_k}$ mit rk die Spannweite der Variable k
Kulczynski	$\frac{n_{11}}{n_{01}+n_{10}}$	Mahalanobis	$\sqrt{(x_i - x_j)^T S^{-1}(x_i - x_j)}$ mit S die Kovarianzmatrix der Variablen xi

Beispiele

• Ein Internetbuchhändler weiß für zwei Besucher, welche Buch-Webseiten sie sich angesehen haben, für jede der p Webseiten wird also eine 0=nicht angesehen oder 1=angesehen gespeichert. Welches Ähnlichkeitsmaß bietet sich an, um zu erfahren, wie ähnlich die beiden Besucher sind? Die Anzahl der Buch-Webseiten, die sich keiner der beiden Besucher angesehen hat ( = n₀₀), von denen es viele gibt, sollten in die Berechnung nicht einfließen. Eine möglicher Koeffizient wäre der Jaccard-Koeffizient, d.h. die Anzahl der Buch-Webseiten, die sich beide Besucher angesehen haben ( = n₁₁), dividiert durch die Anzahl der Buch-Webseiten, die sich mindestens einer der beiden Besucher angesehen hat (n₁₀ Anzahl der Buch-Webseiten, die sich nur der erste Besucher angesehen hat, und n₀₁ Anzahl der Buch-Webseiten, die sich nur der zweite Besucher angesehen hat).
• In den ALLBUS Daten wird u.a. nach der Einschätzung der aktuellen Wirtschaftslage mit den Antwortmöglichkeiten Sehr gut, Gut, Teils-Teils, Schlecht und Sehr Schlecht gefragt. Für jede der möglichen Antworten wird nun eine binäre Variable gebildet, so dass die binären Ähnlichkeitsmaße verwendet werden können. Zu beachten ist, dass bei mehreren Variablen mit unterschiedlichen Kategorienzahl noch eine Gewichtung bzgl. der Kategorienzahl stattfinden sollte.
• Im Iris Datensatz werden die vier ( = p) Abmessungen von Schwertlilienblütenblättern betrachtet. Um Abstände zwischen zwei Blütenblättern i und j zu berechnen, kann z.B. der euklidische Abstand benutzt werden.

Welches Ähnlichkeits- bzw. Distanzmaß verwendet wird, hängt letztlich von der gewünschten inhaltlichen Interpretation des Ähnlichkeits- bzw. Distanzmaßes ab.

Divisive Berechnung

Wie oben angesprochen gibt es theoretisch $\mathcal{O}(2^n)$ Möglichkeiten, einen Datensatz mit n Objekten in zwei Teile zu teilen. Divisive Verfahren brauchen daher normalerweise eine Heuristik, um Kandidaten zu generieren, die dann beispielsweise mit denselben Maßen wie in der agglomerativen Berechnung bewertet werden können.

Effiziente Algorithmen

Während die naive Berechnung einer hierarchischen Clusteranalyse eine schlechte Komplexität hat (bei komplexen Ähnlichkeitmaßen kann eine Laufzeit von O(n³) oder O(n²log n) auftreten), so gibt es für manche Fälle effizientere Lösungen.

So gibt es für single-linkage ein agglomeratives optimal effizientes Verfahren namens SLINK^[1] mit der Komplexität O(n²), und eine Verallgemeinerung davon auf complete-linkage CLINK^[2] ebenfalls mit der Komplexität O(n²). Für andere Fusionierungsmethoden wie Average-Linkage sind keine effizienten Algorithmen bekannt.^[3]

Beispiel

1000 Schweizer Franken Banknote.

Der Schweizer Banknoten Datensatz besteht 100 echten und 100 gefälschten Schweizer 1000 Franken Banknoten. An jeder Banknote wurden sechs Variablen erhoben:

• Die Breite der Banknote (WIDTH),
• die Höhe an der Banknote an der linken Seite (LEFT),
• die Höhe an der Banknote an der rechten Seite (RIGHT),
• der Abstand des farbigen Drucks zur Oberkante der Banknote (UPPER),
• der Abstand des farbigen Drucks zur Unterkante der Banknote (LOWER) und
• die Diagonale (links unten nach rechts oben) des farbigen Drucks auf der Banknote (DIAGONAL).

Als Distanzmaß bietet sich hier die euklidische Distanz an

$d_{ij}=\sqrt{\sum_{k=1}^6 (x_{ik}-x_{jk})^2}$.

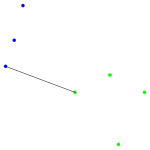
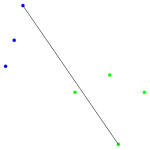
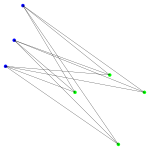
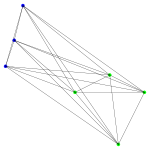
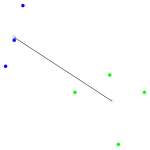
und für die folgende Grafiken wurden dann verschiedene hierarchische Clustermethoden angewandt. Jede Grafik besteht aus zwei Teilen:

• Im linken Teil werden die ersten zwei Hauptkomponenten der Daten gezeigt. Diese Darstellung wird gewählt, weil bei dieser (zweidimensionalen) Darstellung die Abstände in der Fläche gut den Abständen in sechsdimensionalen Raum entsprechen. Gibt es also zwei klar getrennte Cluster (Abstände zwischen den Clustern sind groß), so hofft man diese auch in dieser Darstellung zu sehen. Die Datenpunkte, die zu einem Cluster gehören sind mit der gleichen Farbe markiert; lediglich bei den schwarzen Datenpunkten ist es so, dass jeder Datenpunkt ein Cluster bildet.
• Im rechten Teil sehen wir das zugehörige Dendrogramm. Die "Height" auf der y-Achse gibt bei welcher "Distanz" Beobachtungen bzw. Cluster zu einem neuen Cluster zusammen gefügt werden (entsprechend dem Fusionierungsalgorithmus). Gehören die beiden Teilcluster für eine Fusionierung zum gleichen Cluster ist das Dendrogramm in der entsprechenden Farbe des Clusters gezeichnet; gehören sie zu verschiedene Clustern, dann wird die Farbe schwarz benutzt. Die grauen Punkte links im Dendrogramm geben nochmal an, bei welcher "Distanz" eine Fusionierung stattfand. Um eine gute Clusterzahl zu bestimmen, wird eine möglichst grosse Lücke bei den grauen Punkten gesucht. Denn eine große Lücke bedeutet, dass bei der nächsten Fusionierung eine große Distanz zwischen den zu fusionierenden Clustern besteht.

• 

  Daten und Dendrogramm für das Average linkage Verfahren.

• 

  Daten und Dendrogramm mit der Ward Methode.

• 

  Daten und Dendrogramm für das Complete linkage Verfahren.

• 

  Daten und Dendrogramm für das Single linkage Verfahren.

• 

  Daten und Dendrogramm mit der Median Methode.

• 

  Daten und Dendrogramm mit der Centroid Methode.

Einzelnachweise

1. ↑ R. Sibson: SLINK: an optimally efficient algorithm for the single-link cluster method. In: The Computer Journal. 16, Nr. 1, British Computer Society, 1973, S. 30-34 (http://www.cs.gsu.edu/~wkim/index_files/papers/sibson.pdf (PDF-Datei)).
2. ↑ D. Defays: An efficient algorithm for a complete link method. In: The Computer Journal. 20, Nr. 4, British Computer Society, 1977, S. 364-366.
3. ↑ Johannes Aßfalg, Christian Böhm, Karsten Borgwardt, Martin Ester, Eshref Januzaj, Karin Kailing, Peer Kröger, Jörg Sander, Matthias Schubert, Arthur Zimek: Knowledge Discovery in Databases, Kapitel 5: Clustering. In: Skript KDD I. 2003 (http://www.dbs.ifi.lmu.de/Lehre/KDD/WS1011/skript/kdd-5-clustering4.pdf (PDF-Datei)).

Literatur

Grundlagen und Verfahren

• Ester, M., Sander, J. Knowledge Discovery in Databases. Techniken und Anwendungen, Springer, Berlin, 2000
• Backhaus, K., Erichson, B., Plinke, W., Weiber, R. Multivariate Analysemethoden. Springer
• Bickel, S., Scheffer, T., Multi-View Clustering. Proceedings of the IEEE International Conference on Data Mining, 2004
• Shi, J., Malik, J. Normalized Cuts and Image Segmentation, in Proc. of IEEE Conf. on Comp. Vision and Pattern Recognition, Puerto Rico 1997
• Xu, L., Neufeld, J., Larson, B. and Schuurmans, D., Maximum margin clustering. in Advances in Neural Information Processing Systems 17 (NIPS*2004), 2004

Anwendung

• Bacher, J., Pöge, A., Wenzig, K., Clusteranalyse - Anwendungsorientierte Einführung in Klassifikationsverfahren, 3. Auflage. München, Oldenbourg 2010, 978-3-486-58457-8
• Bortz, J. (1999), Statistik für Sozialwissenschaftler. (Kap. 16, Clusteranalyse). Berlin: Springer
• Härdle, W.; Simar, L. Applied Multivariate Statistical Analysis, Springer, New York, 2003
• Homburg, C., Krohmer. H. Marketingmanagement: Strategie - Instrumente - Umsetzung - Unternehmensführung, 3 Edition, Kapitel 8.2.2, Gabler, Wiesbaden, 2009
• Moosbrugger, H., Frank, D.: Clusteranalytische Methoden in der Persönlichkeitsforschung. Eine anwendungsorientierte Einführung in taxometrische Klassifikationsverfahren. Huber, Bern 1992, ISBN 3-456-82320-7.

Siehe auch

• Clusteranalyse
• Data-Mining
• Knowledge Discovery in Databases
• Klasseneinteilung