p-Wert

Der p-Wert (auch Überschreitungswahrscheinlichkeit, Signifikanzwert; englisch p-value von probability, engl. für Wahrscheinlichkeit) ist eine Kennzahl zur Auswertung statistischer Tests. Er steht in enger Beziehung mit dem Signifikanzniveau, lässt sich aber nicht so einfach in Tabellen fassen, sodass die praktische Anwendung erst mit Einführung von Computern und Statistik-Software möglich geworden ist.

Der p-Wert ist ein Wert zwischen Null und Eins, bestimmt durch die gezogene Stichprobe. Er deutet an, wie glaubhaft es ist, ein solches Stichprobenergebnis zu erhalten, wenn die Nullhypothese wahr ist und damit umgekehrt, wie glaubhaft die Nullhypothese bei Erhalt dieses Stichprobenergebnisses ist. Der p-Wert ist die Wahrscheinlichkeit, unter Gültigkeit der Nullhypothese das erhaltene Ergebnis oder ein extremeres zu erhalten. Mit dem p-Wert wird also angedeutet, wie extrem das Ergebnis ist: je kleiner der p-Wert, desto mehr spricht das Ergebnis gegen die Nullhypothese. Werte kleiner als eine im voraus festgesetzte Grenze, wie 5 %, 1 % oder 0,1 % sind Anlass, die Nullhypothese abzulehnen. Wenn die Nullhypothese verworfen wird, wird das Resultat als statistisch signifikant betrachtet.

Mathematische Formulierung

Bei einem statistischen Test wird eine Vermutung (Nullhypothese) H₀ überprüft, indem ein passendes Zufallsexperiment durchgeführt wird, das die Zufallsgrößen $X_1, X_2, \dots X_n$ liefert. Diese Zufallsgrößen werden zu einer einzelnen Zahl („Statistik“)

$Y=u(X_1,X_2,\dots X_n)$

zusammengefasst. Für einen konkreten Versuchsausgang $x_1, x_2, \dots x_n$ des Experiments erhält man einen Wert

$y=u(x_1,x_2,\dots x_n)$.

Der p-Wert des Versuchsausgangs ist dann die Wahrscheinlichkeit, dass ein zufälliger Versuch bei gültiger Nullhypothese mindestens so „extrem“ ausgeht wie der beobachtete Versuch. Die gewählte "Statistik" ist daher sehr wichtig.

Bei rechtsseitigem Test:

$p_{\text{rechts}}=P(Y\geq y|H_0).$

Bei linksseitigem Test:

$p_{\text{links}}=P(Y\leq y|H_0).$

Und bei zweiseitigem Test:

$p=2\cdot\min(p_{\text{rechts}},p_{\text{links}}).$

Für diese Realisation x im Ablehnbereich K ist der p-Wert kleiner als α

Der p-Wert gibt an, "wie extrem" der auf Basis der erhobenen Daten berechnete Wert der Teststatistik ist. Er entspricht der Wahrscheinlichkeit, bei Gültigkeit der Nullhypothese den errechneten oder einen extremeren Wert der Teststatistik zu erhalten. Für zusammengesetzte Nullhypothesen ist diese bedingte Wahrscheinlichkeit nur noch nach oben abschätzbar.

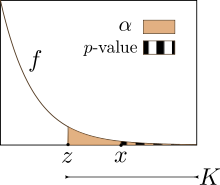
Je kleiner der p-Wert ist, desto mehr Grund gibt es die Nullhypothese zu verwerfen. Üblicherweise wird vor dem Test ein Signifikanzniveau α festgelegt und die Nullhypothese dann verworfen, wenn der p-Wert kleiner oder gleich α ist.

Nach frequentistischer Sichtweise enthält der von R. A. Fischer eingeführte p-Wert keine weiterführende Information, nur die Tatsache, ob er kleiner ist als ein vorgegebenes Niveau α, ist von Interesse. In dieser Form ist $p \le \alpha$ nur eine andere Formulierung dafür, dass die Observation in der kritischen Region liegt und fügt der Neyman-Pearsonschen Theorie der Hypothesentests nichts Neues hinzu.

Beispiel

Gegeben sei eine Münze. Die zu prüfende Nullhypothese sei, dass die Münze fair ist, dass also Kopf und Zahl gleich wahrscheinlich sind; die Alternativhypothese sei, dass ein Ergebnis wahrscheinlicher ist, wobei nicht festgelegt wird, welches der beiden wahrscheinlicher sein soll. Das Zufallsexperiment zum Testen der Nullhypothese bestehe nun darin, dass die Münze zwanzig Mal geworfen wird. K bezeichne die Anzahl der Würfe, die „Kopf“ als Ergebnis liefern. Bei einer fairen Münze wäre zehnmal „Kopf“ zu erwarten. Als Statistik wählt man daher sinnvollerweise

Y = | K − 10 | .

Angenommen, der Versuch liefert k = 14 Mal das Ergebnis „Kopf“, also y = 4. Unter der Nullhypothese ist die Anzahl der Köpfe binomialverteilt mit n = 20 und $p=\tfrac{1}{2}$. Der p-Wert für diesen Versuchsausgang ist daher

$P(Y\geq y|H_0)=P(Y\geq 4|H_0)=\sum_{j=0}^{6}{20\choose j}\frac{1}{2^{20}}+\sum_{j=14}^{20}{20\choose j}\frac{1}{2^{20}}=$

$=2\sum_{j=0}^{6}{20\choose j}\frac{1}{2^{20}}\approx 0{,}115.$

Bei einem Signifikanzniveau von 5 % würde man die Nullhypothese nicht verwerfen, d. h., man kann aus den Daten nicht folgern, dass die Münze nicht fair sei.

Wäre das Versuchsergebnis k = 15 Mal Kopf, also y = 5, dann wäre der p-Wert für diesen Versuchsausgang

$P(Y\geq 5|H_0)=2\sum_{j=0}^{5}{20\choose j}\frac{1}{2^{20}}\approx 0{,}041.$

Bei einem Signifikanzniveau von 5 % würde man also in diesem Fall die Nullhypothese verwerfen, also schließen, dass die Münze nicht fair ist, bei einem Signifikanzniveau von 1 % hingegen weiterhin akzeptieren. (Genauer gesagt: Man würde die Datenlage für unzureichend ansehen, um den Schluss zu rechtfertigen, die Münze sei nicht fair. Dies als einen Beweis zu nehmen, dass die Münze fair ist, wäre jedoch falsch.)

Beziehung zum Signifikanzniveau

Es besteht eine enge Beziehung zwischen dem (beobachteten) p-Wert p und dem (im Voraus gewählten) Signifikanzniveau. Wenn t das Ergebnis der Teststatistik (Prüfgröße) T ist, und k der kritische Wert beim Signifikanzniveau α ist, so gilt z. B. rechtsseitig:

$\!p=P(T\ge t|H_0)$

$\!\alpha = P(T\ge k|H_0)$

und

$p < \alpha \Leftrightarrow t>k$

KS-Test für die Variable „Mittlerer Hauspreis pro Bezirk“ des Boston-Housing-Datensatzes.

In statistischer Software wird bei der Durchführung eines Tests der p-Wert, siehe rechts unter Asymptotische Signifikanz (letzte Zeile im Kasten), angegeben. Ist der p-Wert kleiner als das vorgegebene Signifikanzniveau α, so ist die Nullhypothese abzulehnen.

Auf der einen Seite enthebt die Ausgabe des p-Wertes bei einem Test die Software explizit davon, nach dem vorgegebenen Signifikanzniveau zu fragen, um eine Testentscheidung zu treffen. Auf der anderen Seite besteht die Gefahr, dass der Forscher das eigentlich im voraus festzulegende Signifikanzniveau anpasst, um sein gewünschtes Ergebnis zu bekommen.

Weitere Eigenschaften

Falls die Test-Statistik eine kontinuierliche Verteilung hat, ist der P-Wert, unter der (punktförmigen) Nullhypothese, uniform verteilt auf dem Interval [0,1]. ^[1]

Weblinks

• Kurze Darstellung des p-Wertes auf Englisch (Queen's University, Kingston, Canada)
• CDF Statistics Committee: Simple facts about p-values.. Memo, CDF/MEMO/STATISTICS/PUBLIC/8023. 2006. [1] (englisch, PDF, 113 KiB)
• P-value calculator, Seite zur automatischen Berechnung des p-Werts

Einzelnachweise

1. ↑ Besag, Clifford: Sequential Monte Carlo p-values. In: Biometrika Nr. 78(2), 1991. S. 301-304. doi:10.1093/biomet/78.2.301.