Stetige Gleichverteilung

Dichtefunktion der Gleichverteilung für a = 4,b = 8 (blau), a = 1,b = 18 (grün) und a = 1,b = 11 (rot)

Die stetige Gleichverteilung, auch Rechteckverteilung oder Uniformverteilung genannt, ist eine stetige Wahrscheinlichkeitsverteilung. Sie hat auf einem Intervall (a,b) eine konstante Wahrscheinlichkeitsdichte. Dies ist gleichbedeutend damit, dass alle Teilintervalle gleicher Länge dieselbe Wahrscheinlichkeit besitzen.

Definition

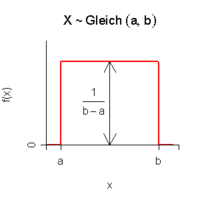
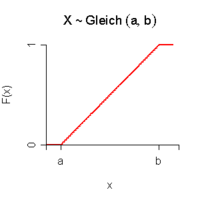
Eine stetige Zufallsvariable X bezeichnet man als gleichverteilt auf dem Intervall [a,b], wenn Dichtefunktion f(x) und Verteilungsfunktion F(x) gegeben sind als

$f(x)=\begin{cases} \frac 1{b-a} & a \le x \le b\\ 0 & \text{sonst} \end{cases}$
$F(x)= \begin{cases} 0 & x \le a\\ \frac{x-a}{b-a} & a < x < b\\ 1 & x\ge b \end{cases}$

Als abkürzende Schreibweise für die stetige Gleichverteilung wird häufig $\mathcal U(a,b)$ oder $\mathcal{SG}(a,b)$ verwendet. In einigen Formeln sieht man auch Gleich(a,b) oder uniform(a,b) als Bezeichnung für die Verteilung.

Eigenschaften

Erwartungswert und Median

Der Erwartungswert und der Median der stetigen Gleichverteilung ist

$\operatorname E(X) = \int\limits_{-\infty}^\infty xf(x)dx = \frac 1{b-a}\int\limits_a^b x\cdot 1dx = \frac 12\frac{b^2-a^2}{b-a} = \frac{a+b}2.$

Varianz

Die Varianz der stetigen Gleichverteilung ist

$\begin{align} \operatorname{Var}(X) &= \operatorname E(X^2) - \left(\operatorname E(X)\right)^2\\ &= \frac 1{b-a}\int\limits_a^b x^2 \cdot 1dx - \left(\frac{a+b}2\right)^2\\ &= \frac 13\frac{b^3-a^3}{b-a} - \left(\frac{a+b}2\right)^2\\ &= \frac 1{12}\left(4b^2 + 4ab + 4a^2 - 3a^2 - 6ab - 3b^2\right)\\ &= \frac 1{12}(b-a)^2. \end{align}$

Standardabweichung

Aus der Varianz erhält man die Standardabweichung

$\sigma_x = \sqrt{\frac{(b-a)^2}{12}} = \frac{b-a}{2\sqrt 3}.$

Variationskoeffizient

Für den Variationskoeffizienten ergibt sich:

$\operatorname{VarK}(X) = \frac 1{\sqrt 3}\frac{b-a}{a+b}.$

Schiefe

Die Schiefe lässt sich darstellen als

$\operatorname v(X) = 0.$

Wölbung und Exzess

Der Wölbung und der Exzess lassen sich ebenfalls geschlossen darstellen als

$\beta_2 = \frac{9}{5} = 1,8$ (Wölbung) bzw.

$\gamma_2 = -\frac 65. = -1,2$ (Exzess).

Momente der Ordnung k

Moment	$m_k = \frac{1}{k+1}\sum_{i=0}^k a^i b^{k-i}$
Zentrales Moment	$\mu_k = \begin{cases}\frac{(b-a)^k}{2^k(k+1)} & \text{ k gerade}\\ 0 & \text{ k ungerade}\end{cases}$

Summe gleichverteilter Zufallsvariablen

Verteilungsdichten der Summe von bis zu 6 Gleichverteilungen U(0,1)

Die Summe zweier identischer unabhängiger und stetig gleichverteilter Zufallsvariablen ist dreiecksverteilt; die Summe der Gleichverteilungen zu Intervallen [a,b] bzw. [c,d] mit $b-a \neq d-c$ besitzt dagegen eine trapezförmige Verteilung. Wegen des Zentralen Grenzwertsatzes nähert sich die Summe von unabhängigen gleichverteilten Zufallsvariablen umso mehr der Normalverteilung an, je mehr Zufallsvariablen aufsummiert werden.

Eine zuweilen verwendete Methode (Zwölferregel) zur approximativen Erzeugung (standard-)normalverteilter Zufallszahlen funktioniert so: man summiert 12 (unabhängige) auf dem Intervall [0,1] gleichverteilte Zufallszahlen und subtrahiert 6 (das liefert die richtigen Momente, da die Varianz einer U(0,1)-verteilten Zufallsvariablen 1/12 ist und sie den Erwartungswert 1/2 besitzt).

Charakteristische Funktion

Die charakteristische Funktion hat die Form

$\phi_X(t) = \frac{1}{(b-a)it}\left(e^{itb}-e^{ita}\right)$,

wobei i die imaginäre Einheit darstellt.

Momenterzeugende Funktion

Die momenterzeugende Funktion der stetigen Gleichverteilung ist

$m_X(s) = \begin{cases}\frac{\displaystyle e^{bs}-e^{as}}{\displaystyle (b-a)s} & s\neq 0 \\ 1 & s=0. \end{cases}$

und speziell für a = 0 und b = 1

$m_X(s) = \frac 1s(e^s-1).$

Damit ergeben sich die ersten allgemeinen Momente zu

$m_1 = \frac 12(a+b).$

Beziehung zu anderen Verteilungen

Mit der Inversionsmethode lassen sich gleichverteilte Zufallszahlen in andere Verteilungen überführen. Wenn X eine gleichverteilte Zufallsvariable ist, dann genügt beispielsweise $Y=-\tfrac 1g \ln(X)$ der Exponentialverteilung mit dem Parameter g.

Beispiel für das Intervall [0,1]

Häufig wird a = 0 und b = 1 angenommen, also $X=\mathcal U(0,1)$ betrachtet. Dann ist die Dichtefunktion f(x) = 1 und die Verteilungsfunktion F(x) = x auf dem Intervall [0,1]. Der Erwartungswert beträgt E(X) = 0,5 und die Varianz Var(X) = 1/12, somit ist die Standardabweichung $\sigma = \sqrt{1/12} \approx 0{,}29$. Siehe hierzu auch den obigen Abschnitt Summe gleichverteilter Zufallsvariablen.

Siehe auch

• Diskrete Gleichverteilung

Weblinks

• Universität Konstanz – Interaktive Animation

Diskrete univariate Verteilungen

Diskrete univariate Verteilungen für endliche Mengen:
Benford | Bernoulli | beta-binomial | binomial | kategorial | hypergeometrisch | Rademacher | Zipf | Zipf-Mandelbrot

Diskrete univariate Verteilungen für unendliche Mengen:
Boltzmann | Conway-Maxwell-Poisson | negativ binomial | erweitert negativ binomial | Compound-Poisson | diskret uniform | discrete-Phase-Type | Gauss-Kuzmin | geometrisch | logarithmisch | parabolisch-fraktal | Poisson | Poisson-Gamma | Skellam | Yule-Simon | Zeta