- Schergesetz
-
Dieser Artikel wurde den Mitarbeitern der Redaktion Physik zur Qualitätssicherung aufgetragen. Wenn Du Dich mit dem Thema auskennst, bist Du herzlich eingeladen, Dich an der Prüfung und möglichen Verbesserung des Artikels zu beteiligen. Der Meinungsaustausch darüber findet derzeit nicht auf der Artikeldiskussionsseite, sondern auf der Qualitätssicherungs-Seite der Physik statt.
Ein Schergesetz gibt in den Materialwissenschaften an, wie sich ein Material unter dem Einfluss von Scherkräften verhält. Schergesetze werden in technischen Gebieten wie Maschinenbau und Bauwesen verwendet, um die maximale Belastbarkeit einer Konstruktion abzuschätzen. In der Geotechnik dienen sie zur Bestimmung der maximalen Tragfähigkeit des Bodens und zur Vorhersage von Setzungen.
Inhaltsverzeichnis
Schergesetz von Charles Augustin de Coulomb
Schergesetz von Coulomb. Bei Scherspannungen oberhalb der blauen Linie kommt es zu bleibenden Verformungen.
Bei einer Scherung eines Körpers treten sowohl Spannungen in Richtung der Scherung als auch solche senkrecht dazu auf. Eine Spannung senkrecht zur Scherung wirken hemmend auf die Scherung. Je größer sie ausfällt, desto größer kann die Scherspannung τ werden bevor eine dauerhafte Verformung eintritt. Dies ist ähnlich wie bei der Reibung, die in der Lage ist, einen Körper auf einer schiefen Ebene an der Bewegung zu hindern. Zusätzlich kann zwischen Körnern, oder Molekülen des Körpers eine Haltekraft wirken, die überwunden werden müssen, bevor ein Teil des Körpers abschert. Die durch diese Kräfte bewirkte Spannung wird Kohäsion genannt.
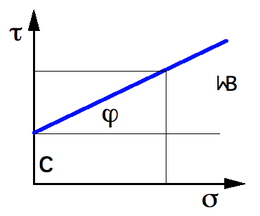
Die Spannung τscher, oberhalb der eine dauerhafte Verformung eintritt, kann für ein bestimmtes Material mit dem Schergesetz von Coulomb bestimmt werden:
Dabei ist c die vom Material abhängige Kohäsion und φ ein ebenfalls vom Material abhängiger Parameter. Die senkrecht zur Scherung wirkende Spannung σ ist proportional zum Druck an der betrachteten Stelle im Körper.
Mit diesem Schergesetz werden alle Böden und auch Felsen beschrieben. Auch für Metalle und bei anderen natürlichen Stoffen (Schütt- und Lagerstoffe mit fester Konsistenz) ist es anwendbar.
Anwendung auf Böden mit Porenwasser
Eine Besonderheit bei körnigen Medien wie Boden ist das Porenwasser. Drückt man auf einen trockenen Boden, so werden hauptsächlich die Poren zusammengedrückt. Die einzelnen Körner rücken damit näher zusammen und übernehmen den Druck. Sind nun die Poren mit Wasser gefüllt, ist die Situation etwas komplizierter. Das Wasser ist inkompressibel und nimmt zuerst die äußere Belastung als Porenwasserdruck auf. Da seitlich der Last ein geringerer Porendruck herrscht, fließt das Wasser zum niedrigen Druck ab und die Poren können sich deformieren (verringern) und so kann die Belastung auf die Körner des Bodens abgeleitet werden. Diesen Vorgang nennt man Konsolidieren des Bodens. Der Porenwasserdruck, der durch die Belastung entsteht, nennt man Porenwasserüberdruck. Dieser wird bei der Konsolidierung abgebaut.
Bei einem wassergesättigten Boden werden die Gewichtskräfte von Korn zu Korn übertragen. Diese Übertragung erfolgt nach dem Stoffgesetz von Coulomb. Wird nun ein wassergesättigter Boden durch eine Zusatzlast belastet, so entsteht durch die Zusatzlast ein Porenwasserüberdruck. Das Korngerüst spürt vorerst nichts von dieser Zusatzbelastung, da das Wasser den Druck aufnimmt. So ist die Korn zu Kornspannung im ersten Moment gleich groß wie ohne Zusatzbelastung. Erst mit der Zeit, wenn das Porenwasser abrinnt, werden die Korn zu Kornspannungen sich so vergrößern, bis die Zusatzspannung voll von der Korn zu Kornspannung aufgenommen wird. Dies muss also auch beim Schergesetz berücksichtigt werden. Das Schergesetz von Coulomb gilt aber nur für Korn zu Kornspannungen. Es muss der Porenwasserüberdruck noch von der Gesamtspannung abgezogen werden.
σ' = σ – u
σ' = Korn zu Kornspannung u = Porenwasserüberdruck σ = Gesamtspannung
damit kommt man zum erweiterten Stoffgesetz von Coulomb:
τ = c + σ' * tan ϕ bzw.
τ = c + (σ – u) * tan ϕ
Siehe auch
Literatur
- Bernhard Wietek: Grundbau – Einführung in Theorie und Praxis. 4. Auflage; Manz-Verlag, Wien 2004, ISBN 978-3706812061
- Bernhard Wietek: Stahlfaserbeton. 2. Auflage; Vieweg+Teubner Verlag 2010, ISBN 978-3834805928
Wikimedia Foundation.
