Cobb-Douglas-Produktionsfunktion

Die Cobb-Douglas-Funktion, eine Spezialfunktion der CES-Produktionsfunktion, wird sowohl in der Mikro- und Makroökonomie als auch in der Produktionswirtschaft häufig verwendet. Sie wird sowohl als Nutzen- als auch als Produktionsfunktion eingesetzt.

Geschichte

Die Cobb-Douglas-Funktion basiert auf Erkenntnissen, die Johann Heinrich von Thünen bereits in der ersten Hälfte des 19. Jahrhunderts in der Landwirtschaft sammelte. Knut Wicksell (1851–1926) gelang es 1913 die Zusammenhänge zwischen Input und Output bei einer vorhandenen Substitutionselastizität in einer speziellen Produktionsfunktion konkreten zu formulieren, die schließlich von den US-amerikanischen Ökonomen Paul Howard Douglas und Charles Wiggins Cobb im Jahre 1928 statistisch nachgewiesen wurde.

allgemeine Form

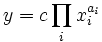$y=c\prod_i x_i^{a_i}$ mit c, a_i > 0

c ist ein Niveauparameter, der bei geeigneter Normierung von y aber verzichtbar ist. Die a_i sind die partiellen Elastizitäten von y bzgl. x_i.

Die Funktion ist homogen vom Grad $\sum a_i$.

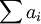Die Funktion wird als Beispiel für Nutzenfunktionen sowie als Produktionsfunktion eingesetzt.

Cobb-Douglas-Nutzenfunktion

Nachfragefunktionen, die aus einer Cobb-Douglas-Nutzenfunktion gewonnen werden, haben die Eigenschaft, dass die Haushalte für die Güter x_i immer einen konstanten Anteil a_i ÷ 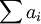$\sum a_i$ von ihrem Einkommen ausgeben. Es gilt das Gesetz der abnehmenden Grenzrate der Substitution.U(c,g).

Beispiel einer Cobb-Douglas-Nutzenfunktion: u(x,y) = x^c * y^d

Im obigen Zweigüterfall ist die Grenzrate der Substitution $GRS=\frac{c}{d}\frac{y}{x}$.

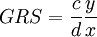Cobb-Douglas-Produktionsfunktion

Meist in der Form $Y = c \cdot K^a \cdot L^b$.

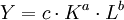• Y: Produktionsmenge
• c: Nichtkonstanter Faktor. Ist c nicht konstant, sondern wird mit der Zeit größer, dann kann so technischer Fortschritt abgebildet werden. Als Faktor vor der gesamten Produktionsfunktion wie hier bildet c(t) (t = Zeit) Hicks-neutralen technischen Fortschritt ab.
• K: Kapitalstock
• L: Arbeitseinsatz

Die partiellen Produktionselastizitäten lassen sich als a und b ebenso wie die Skalenelastizität a + b unmittelbar ablesen. Abnehmende Grenzproduktivitäten liegen vor, wenn a,b < 1.

Die Exponenten einer Cobb-Douglas-Produktionsfunktion müssen sich nach aktuellen Erkenntnissen nicht immer zu 1 addieren lassen, obwohl dies den Regelfall darstellt (a + b = 1). Werden K und L um einen bestimmten Prozentsatz erhöht, erhöht sich die Ausbringung Y um denselben Prozentsatz.

Linear-homogene Cobb-Douglas-Produktionsfunktion

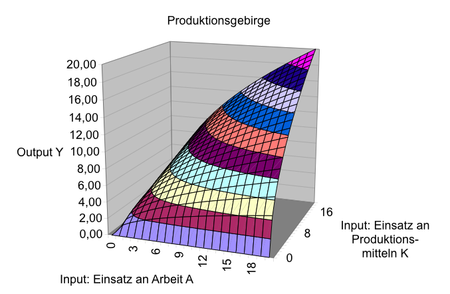
In der Abbildung ist eine linear homogene Cobb-Douglas-Produktionsfunktion als "Produktionsgebirge" dargestellt. Die Fläche des Gebirges setzt sich aus Geraden zusammen, die vom Ursprung (0,0,0) ausgehen. Hält man einen Produktionsfaktor konstant und erhöht den anderen Produktionsfaktor, dann erhöht sich auch der Output, aber in immer geringerem Maße, die partielle Grenzproduktivität eines Faktors nimmt mit steigender Einsatzmenge dieses Faktors ab. Die partielle Grenzproduktivität ist die Steigung des Produktionsgebirges, wenn man sich auf ihm senkrecht zur Achse des konstant gehaltenen Produktionsfaktors bewegt.

Bewegt sich die Volkswirtschaft entlang einer "Höhenlinie", dann wird der Einsatz eines Produktionsfaktors durch den des anderen substituiert. Es gilt das Gesetz von der abnehmenden Grenzrate der technischen Substitution.

Literatur

• Charles W. Cobb, Paul H. Douglas: „A Theory of Production“ in American Economic Review, March 1928 Supplement, Vol. 18 Issue 1, S. 139-165.

Weblinks

• Graphische Darstellung verschiedener Typen von Cobb-Douglas-Funktionen (in Englisch)