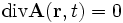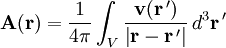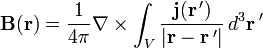Coulombeichung

Die Coulomb-Eichung (auch Strahlungseichung oder transversale Eichung) stellt eine mögliche Einschränkung des Vektorpotentials 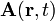$\mathbf A (\mathbf r,t)$ dar. Die Variable 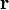$\mathbf r$ ist eine vektorielle Größe und repräsentiert den Ort. Die skalare Variable t steht für die Zeit. Auf Grund der Coulomb-Eichung wird das Vektorpotential 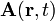$\mathbf A (\mathbf r,t)$ so gewählt, dass

${\rm div} \mathbf A (\mathbf r,t)=0$

gilt, d.h. dass die Divergenz des Vektorpotentials 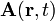$\mathbf A (\mathbf r,t)$ verschwindet.

Für ein zeitlich konstantes Vektorfeld 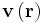$\mathbf v \,(\mathbf r)$ im $\mathbb{R}^3$, das im Unendlichen gegen Null geht, führt folgende Coulomb-Eichung zum gesuchten Potential:

$\mathbf A (\mathbf r)= \frac{1}{4\pi} \int_{V} \frac{\mathbf v(\mathbf r \,')}{\left|\mathbf r-\mathbf r \,'\right|}\,d^3\mathbf r \,'$

Zur Lösung der Maxwell-Gleichungen, der Grundgleichungen der Theorie des Elektromagnetismus, werden üblicherweise Potentialfunktionen eingeführt, nämlich das skalare Potential 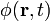$\phi(\mathbf r,t)$ und das Vektorpotential 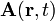$\mathbf A (\mathbf r,t)$. Die Potentialfunktionen sind lediglich Hilfsfunktionen zur Lösung der Maxwell-Gleichungen. Das Vektorpotential 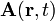$\mathbf A (\mathbf r,t)$ wird durch die folgende Gleichung definiert:

$\mathbf B (\mathbf r,t)= {\rm {rot}} \mathbf A (\mathbf r,t)$.

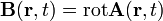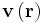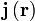
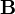also mit $\mathbf v \,(\mathbf r)$ gleich der Ladungsstromdichte $\mathbf j \,(\mathbf r)$

$\mathbf B (\mathbf r)= \frac{1}{4\pi} \mathbf \nabla \times \int_{V} \frac{\mathbf j(\mathbf r \,')}{\left|\mathbf r-\mathbf r \,'\right|}\,d^3\mathbf r \,'$

$\mathbf B$ repräsentiert die magnetische Induktion am Ort 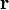$\mathbf r$ zum Zeitpunkt t. Die Rotation des Vektorpotentials 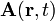$\mathbf A (\mathbf r,t)$ erzeugt die magnetische Induktion $\mathbf B (\mathbf r,t)$.

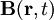Das skalare Potential 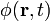$\phi(\mathbf r,t)$ wird durch folgende Gleichung definiert:

$\mathbf E (\mathbf r,t)=-{\rm grad}\phi(\mathbf r,t)-\frac{{\partial\mathbf A}(\mathbf r,t)}{\partial t}$.

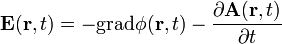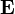$\mathbf E$ repräsentiert das elektrische Feld am Ort 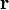$\mathbf r$ zum Zeitpunkt t. Der negative Gradient des skalaren Potentials 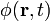$\phi(\mathbf r,t)$ und die negative partielle Ableitung des Vektorpotentials 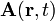$\mathbf A (\mathbf r,t)$ nach der Zeit erzeugen das elektrische Feld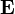 $\mathbf E$

Das Vektorpotential 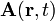$\mathbf A (\mathbf r,t)$ wird durch die vorstehende Definition und die Maxwell-Gleichungen nicht eindeutig festgelegt. Die Maxwell-Gleichungen lassen eine Menge von Lösungen für das Vektorpotential 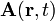$\mathbf A (\mathbf r,t)$ und das skalare Potential 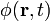$\phi(\mathbf r,t)$ zu. Sofern eine bestimmte Lösung für das Vektorpotential gefunden wurde, können daraus durch Eichtransformation weitere Lösungen erzeugt werden. Die Eichtransformationen haben keine Auswirkung auf die resultierenden elektrischen und magnetischen Felder; sie haben keinerlei physikalische Auswirkung. Die zusätzlichen unphysikalischen Freiheitsgrade können durch Eichung des Vektorpotentials festgelegt werden. Zu den bekannten Eichungen in der Elektrodynamik zählen die Coulomb-Eichung und die Lorenz-Eichung.

Die Coulomb-Eichung legt nicht nur das Vektorpotential sondern auch das skalare Potential fest. Die Lösung für das skalare Potential 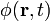$\phi(\mathbf r,t)$ entspricht im Falle der Coulomb-Eichung dem Coulomb-Potential, welches das Potential einer elektrostatischen Ladungsverteilung beschreibt. Daher rührt der Name Coulomb-Eichung.