Gradient (Mathematik)

Zwei Skalarfelder dargestellt als Grauschattierung (dunklere Färbung entspricht größerem Funktionswert). Die blauen Pfeile darauf symbolisieren den zugehörigen Gradienten.

Der Gradient ist ein mathematischer Operator, genauer ein Differentialoperator, der auf ein Skalarfeld angewandt werden kann und in solchem Fall ein Gradientenfeld genanntes Vektorfeld liefert, das die Änderungsrate und Richtung der größten Änderung des Skalarfeldes angibt.

Interpretiert man beispielsweise die Reliefkarte einer Landschaft als eine Funktion h(x,y), die jedem Ort die Höhe an dieser Stelle zuordnet, dann ist der Gradient von h an der Stelle (x,y) ein Vektor in der x-y-Ebene, der in die Richtung des steilsten Anstiegs von h an dieser Stelle zeigt und dessen Länge ein Maß für die Steilheit (Steigung) ist. Zur besseren Abgrenzung zwischen Operator und Resultat seiner Anwendung bezeichnet man solche Gradienten skalarer Feldgrößen in manchen Quellen auch als Gradientvektoren. ^[1]

Der Gradient wird zusammen mit anderen Differentialoperatoren wie Divergenz und Rotation in der Vektoranalysis, einem Teilgebiet der mehrdimensionalen Analysis untersucht. Sie werden mit dem gleichen Vektoroperator gebildet, und zwar mit dem sog. Nabla-Operator $\nabla\,$ (um anzudeuten, dass der Nabla-Operator ein Vektor ist, bisweilen auch $\vec{\nabla}$ oder $\underline \nabla$).

Gradient

Definition

Auf $\R^{n}$ sei das Skalarprodukt $\langle.,.\rangle$ gegeben. Der Gradient der partiell differenzierbaren Funktion $\ f: \R^n \to \R$ im Punkt $a \in \R^n$ ist der durch die Forderung

$\mathrm{d} f(a) h = \langle \nabla f(a) , h \rangle$

eindeutig bestimmte Vektor $\nabla f(a)$. Der Operator d ist die totale Ableitung. Im Fall des Standardskalarproduktes ist $\nabla f(a)$ der Spaltenvektor

$\nabla f=\operatorname{grad}(f)=\frac{\partial f}{\partial x_{1}}\hat{e}_{1}+\cdots+\frac{\partial f}{\partial x_{n}}\hat{e}_{n}=\begin{pmatrix}\frac{\partial f}{\partial x_{1}}\\ \vdots\\ \frac{\partial f}{\partial x_{n}}\end{pmatrix};$

gesprochen "Nabla-f(a)". Die Einträge $\tfrac{\partial f}{\partial x_i}$ sind die partiellen Ableitungen von f in x_i Richtung. Der Gradient hat auch Darstellungen bezüglich anderer Koordinaten, welche zumeist in der Physik betrachtet werden.

Darstellung in drei Dimensionen

• Darstellung in kartesischen Koordinaten : $V = V\left(x;y;z \right)$

$\operatorname{grad}\, V=\nabla V=\frac{{\partial V}}{{\partial x}}\hat{e}_{x}+\frac{{\partial V}}{{\partial y}}\hat{e}_{y}+\frac{{\partial V}}{{\partial z}}\hat{e}_{z}$

• Darstellung in Zylinderkoordinaten : $V = V\left( \rho;\varphi ;z \right)$

$\operatorname{grad}\, V=\nabla V=\frac{{\partial V}}{{\partial\rho}}\hat{e}_{\rho}+\frac{1}{\rho}\frac{{\partial V}}{{\partial\varphi}}\hat{e}_{\varphi}+\frac{{\partial V}}{{\partial z}}\hat{e}_{z}$

• Darstellung in Kugelkoordinaten : $V = V\left( r;\vartheta ;\varphi \right)$

$\operatorname{grad}\, V=\nabla V=\frac{{\partial V}}{{\partial r}}\hat{e}_{r}+\frac{1}{r}\frac{{\partial V}}{{\partial\vartheta}}\hat{e}_{\vartheta}+\frac{1}{{r\sin\vartheta}}\frac{{\partial V}}{{\partial\varphi}}\hat{e}_{\varphi}$

Dies sind Spezialfälle des Gradienten auf riemannschen Mannigfaltigkeiten. Für diese Verallgemeinerung siehe unter äußere Ableitung nach.

Orthogonale Koordinaten

In allgemeinen orthogonalen Koordinaten hat der Gradient die Darstellung

$\mathrm{grad\,\,}f = \nabla f = \sum_{a}{\frac{1}{h_a}\frac{\partial f}{\partial{q_a}}\,\hat{{e}}_{q_a}}\,,$

wobei die h_a den Betrag und $\hat e_{q_a}$ die Richtung des Vektors $\frac{\partial \vec r}{\partial{q_a}}$ angeben.

Geometrische Interpretation

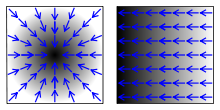
Geometrisch betrachtet ist der Gradient eines Skalarfelds an einem Punkt ein Vektor, der in Richtung des steilsten Anstieges des Skalarfeldes weist. Dabei entspricht der Betrag des Vektors der Stärke des Anstieges. Befindet man sich an einem lokalen Minimum oder Maximum (Extremum) oder einem Sattelpunkt, so ist der Gradient an dieser Stelle gerade der Nullvektor, vorausgesetzt, dass dieser Extrempunkt im Inneren des betrachteten Gebietes liegt.

Mit Hilfe des Gradienten lässt sich auch der Anstieg in jeder beliebigen Richtung, Richtungsableitung genannt, ermitteln, der – im Unterschied zum Gradienten – wieder ein Skalar ist.

Richtungsableitung

Hauptartikel: Richtungsableitung

Unter der Richtungsableitung versteht man die Ableitung, also den Anstieg eines Skalarfeldes $\varphi\left(\vec r\right)$ in Richtung eines normierten Vektors $\vec v$, genauer

$D_{\vec v} \varphi = \frac{\partial\varphi}{\partial\vec v}=\lim_{t\to 0}\frac{\varphi(\vec r+t\vec v)-\varphi(\vec r)}t.$

Ist φ in einer Umgebung von $\vec r$ differenzierbar, dann kann man die Richtungsableitung berechnen als das Skalarprodukt aus $\vec v$ und dem Gradienten von φ.

$D_{\vec v} \varphi = {{\partial\varphi} \over {\partial\vec v}}=\left\langle\mathrm{grad}\,\varphi,\vec v\right\rangle$

Totales Differential

Vollständiges oder totales Differential eines dreidimensionalen Skalarfeldes

$\mathrm d \varphi = \frac{\partial\varphi}{\partial x} \mathrm{d} x + \frac{\partial\varphi}{\partial y}\mathrm{d} y + \frac{\partial\varphi}{\partial z} \mathrm{d}z = \operatorname{grad}\,\varphi\cdot\mathrm{d}\vec{r},\qquad\text{wobei}\quad \mathrm{d}\vec{r} = \begin{pmatrix}\mathrm{d}x\\\mathrm{d}y\\\mathrm{d}z\end{pmatrix}.$

Die Verallgemeinerung auf n Dimensionen ist offensichtlich.

Vektorgradient

In der Mathematik ist der Gradient nur für Funktionen mit Bildbereich in $\mathbb R$ definiert. In der Physik und den Ingenieurswissenschaften wird jedoch ein sogenannter Vektorgradient auch für Funktionen $\vec F:\mathbb R^n\rightarrow\mathbb R^m$ eingeführt. Dieser im folgenden definierte Vektorgradient ist mit der Jacobi-Matrix identisch.

Für $\vec v \in \mathbb R^n$ (mit Standardskalarprodukt) ist

$(\vec{v}\cdot\nabla)\vec{F} = J_\vec{F}\,\vec{v}$

eine Funktion $\mathbb R^n \to \mathbb R^m$, deren Komponenten die Änderung der Komponenten von $\vec F$ in Richtung von $\vec v$ beschreiben. Schreibt man statt $\nabla$ nun $\operatorname{grad}$ und unterdrückt die Klammern, so ergibt sich der sogenannte Vektorgradient $\operatorname{grad}\,\vec{F}$ über die definierende Eigenschaft

$\vec{v}\cdot\operatorname{grad}\,\vec{F} := J_\vec{F}\,\vec{v}.$

Dabei bezeichnet $J_\vec{F}\,\vec{v}=J_\vec{F}\cdot\vec{v}$ die Matrizenmultiplikation der Jacobi-Matrix $J_{\vec{F}}$, einer $m\times n$-Matrix, mit dem Spaltenvektor $\vec{v}$, also einer $n\times 1$-Matrix.

Dass diese Definition keine mathematisch sinnvolle Verallgemeinerung des Gradienten sein kann zeigt sich z.B. dadurch, dass die Definition der Jacobi-Matrix unabhängig vom Skalarprodukt ist, während dieses in die Definition des Gradienten wesentlich eingeht.

Der Vektorgradient lässt sich als transponiertes dyadisches Produkt des Nabla-Operators und eines Vektors auffassen:

$\operatorname{grad}\,\vec{F}=(\nabla\otimes\vec{F})^{T}=(\nabla\vec{F})^{T}$

In Indexschreibweise:

$(\operatorname{grad}\,\vec{F})_{ij}=\frac{\partial F_i}{\partial x_j}$

Der Vektorgradient wird u. a. in der Kontinuumsmechanik (z.B. in den Navier-Stokes-Gleichungen) benutzt.

In der Literatur gibt es auch andere Definitionen des Vektorgradienten, nämlich als transponierte Jacobimatrix $\operatorname{grad}\,\vec{F} := J_\vec{F}^{T}$ oder als das Skalarprodukt eines Vektors mit dem Nablaoperator $\operatorname{grad}\,\vec{F}:= (\vec{v}\cdot\nabla)\vec{F}$.

Totales Differential

Betrachte für ein Vektorfeld eine infinitesimale Verschiebung:

$\vec{F}(\vec{r}+\mathrm{d}\vec{r})=\vec{F}(\vec{r})+J_{\vec{F}}\cdot\mathrm{d}\vec{r}=\vec{F}(\vec{r})+(\operatorname{grad}\vec{F})\cdot\mathrm{d}\vec{r}=\vec{F}(\vec{r})+(\mathrm{d}\vec{r}\cdot\nabla)\vec{F}=\vec{F}(\vec{r})+\mathrm{d}\vec{F}$

Das vollständige oder totale Differential eines Vektorfeldes $\vec{F}(\vec{r})$ ist:

$\mathrm{d}\vec{F}=(\operatorname{grad}\vec{F})\cdot\mathrm{d}\vec{r}$   bzw. in Indexschreibweise   $\mathrm{d}F_{i}=\sum_{j}\frac{\partial F_{i}}{\partial x_{j}}\mathrm{d}x_{j}$

Das totale Differential eines Skalarfeldes und eines Vektorfeldes haben somit dieselbe Form.

Rechenregeln

Gradient

Für alle Konstanten $c\in\R$ und Skalarfelder $u,v:\R^n\to\R$ gilt:

$\operatorname{grad}\,c=\vec{0}$

Linearität

$\operatorname{grad}\,(c\cdot u)=c\cdot\operatorname{grad}\,u$

$\operatorname{grad}\,(u+v)=\operatorname{grad}\,u+\operatorname{grad}\,v$

Produktregel

$\operatorname{grad}\,(u\, v) = u\ \operatorname{grad}\,v + v\ \operatorname{grad}\,u$

$\operatorname{grad}\,(u^n) = n\, u^{n-1}\ \operatorname{grad}\,u$     für   $n\neq 0$

Vektorgradient

Die Rechenregeln sind diejenigen der Jacobi-Matrix. $\operatorname{grad}\vec{A}$ bezeichnet hier den Vektorgradienten.

Für alle Konstanten $c\in\R$, Vektorfelder $\vec{A},\,\vec{B}:\mathbb R^n\rightarrow\mathbb R^m$ und Skalarfelder $u:\R^n\to\R$ gilt:

Linearität

$\operatorname{grad}\,(c\cdot\vec{A})=c\cdot\operatorname{grad}\,\vec{A}$

$\operatorname{grad}\,(\vec{A}+\vec{B})=\operatorname{grad}\,\vec{A}+\operatorname{grad}\,\vec{B}$

Produktregel

$(\vec{A}\cdot\nabla)\vec{B}=(\operatorname{grad}\,\vec{B})\cdot\vec{A}$

$\operatorname{grad}(\vec{A}\cdot\vec{B})=(\operatorname{grad}\,\vec{A})^{T}\cdot \vec{B}+(\operatorname{grad}\,\vec{B})^{T}\cdot\vec{A}$

$\operatorname{grad}(\vec{A}^{\,2}) =2\,(\operatorname{grad}\,\vec{A})^{T}\cdot\vec{A}$

Speziell für Vektorfelder $\vec{A},\,\vec{B}:\mathbb R^3\rightarrow\mathbb R^3$ lassen sich obige Beziehung noch umformen:

$\operatorname{grad}(\vec{A}\cdot\vec{B}) =(\vec{B}\cdot\nabla)\vec{A}+\vec{B}\times(\nabla\times\vec{A})+(\vec{A}\cdot\nabla)\vec{B}+\vec{A}\times(\nabla\times\vec{B})$

$\operatorname{grad}(\vec{A}^{\,2}) =2(\vec{A}\cdot\nabla)\vec{A}+2\vec{A}\times(\nabla\times\vec{A})$

Anwendungen

• Hydrodynamik

Die Strömungsfelder sogenannter Potentialströmungen sind Gradientenfelder.

• Thermodynamik

Sind Teile eines Körper unterschiedlich heiß, so strömt Wärme von den heißeren zu den kühleren Bereichen. Ist die Wärmeleitfähigkeit überall gleich, so ist der Wärmestrom ein Vielfaches des Temperaturgradienten. Für den Wärmestrom j_w gilt also beispielsweise $\mathbf{j_w}=-\lambda\,\mathrm{grad}\,\,T\,,$ mit der sog. „Wärmeleitfähigkeit“ λ.

• Akustik

Der Druckgradient ist das Verhältnis von Druckdifferenz und dem Abstand zweier Punkte. Bei Richtmikrofonen im Schallfeld hat dieser Begriff eine besondere Bedeutung.

• Elektrodynamik

Statische elektrische Felder E sind stets Gradientenfelder elektrostatischer Potentiale $\,\phi (x,y,z)$ ; präziser gilt mit einem Minuszeichen :   $\mathbf E(x,y,z)=-\mathrm{grad}\,\,\phi (x,y,z)\,.$

• Mechanik

Hier gilt Analoges für sog. „konservative Kraftfelder“.

Integrabilitätsbedingung

Eine wichtige Beziehung für Gradientenfeldern in n Dimensionen , $\mathbf G(x_1, ... , x_n)=\mathrm{grad\,\,} f(x_1,...,x_n)\,,$ ist die Aussage, dass diese immer „integrabel“ sind, und zwar in folgendem Sinne: Es gilt für alle i und k   (=1, ...,n):   $\frac{\partial G_i}{\partial x_k}-\frac{\partial G_k}{\partial x_i}\equiv 0\,.$ Diese direkt nachprüfbare Beziehung - in drei Dimensionen identisch mit der Rotationsfreiheit des Feldes - ist notwendig für die Existenz einer „Potentialfunktion“ $\,f$ (präziser: der Funktion $\,\phi =-f$). Die G_i bzw. G_k sind die Komponenten des Vektorfeldes. Die Integrabilitätsbedingung impliziert ferner, dass für alle  geschlossenen Wege W im $\mathbb R^n$ das Linienintegral $\oint_W \mathbf G\cdot\mathrm d\mathbf r$ verschwindet, was in der Mechanik bzw. der Elektrodynamik große Bedeutung hat.

Beispiele

Folgende Gradienten treten häufig in der Physik auf. Es wird der Ortsvektor $\vec{r}=r\hat{e}_{r}$ verwendet.

Gradient

$\operatorname{grad}\, r=\hat{e}_{r}=\frac{\vec{r}}{r}$

$\operatorname{grad}\, U(r)=\frac{\partial U}{\partial r}\hat{e}_{r}$

$\operatorname{grad}\,\frac{1}{r}=-\frac{1}{r^{2}}\,\operatorname{grad}\, r=-\frac{\hat{e}_{r}}{r^{2}}=-\frac{\vec{r}}{r^{3}}$

$\operatorname{grad}\,\frac{1}{|\vec{r}-\vec{r}^{\,\prime}|}=-\frac{1}{|\vec{r}-\vec{r}^{\,\prime}|^{2}}\,\operatorname{grad}\,|\vec{r}-\vec{r}^{\,\prime}|=-\frac{\vec{r}-\vec{r}^{\,\prime}}{|\vec{r}-\vec{r}^{\,\prime}|^{3}}$

Man beachte, dass beim letzten Beispiel der Gradient nur auf $\vec{r}$ und nicht auf $\vec{r}^{\,\prime}$ wirkt. Er wird deshalb auch als $\nabla_{\vec{r}}$ geschrieben.

Vektorgradient

$\operatorname{grad}\, \vec{r}=I$     wobei I die Einheitsmatrix ist.

$(\operatorname{grad}\frac{\vec{r}}{r^{3}})^{T}=\nabla\otimes\frac{\vec{r}}{r^{3}}=(\nabla\frac{1}{r^{3}})\otimes\vec{r}+\frac{1}{r^{3}}(\nabla\otimes\vec{r})=-\frac{3}{r^{5}}\vec{r}\otimes\vec{r}+\frac{1}{r^{3}}I=-\frac{1}{r^{5}}(3\vec{r}\otimes\vec{r}+r^{2}I)$

Die beiden Formeln werden z. B. bei der kartesischen Multipolentwicklung verwendet.

Literatur und Einzelnachweise

• Adolf J. Schwab: Begriffswelt der Feldtheorie, Springer Verlag, ISBN 3-540-42018-5
• Konrad Königsberger: Analysis 2. Springer-Verlag, Berlin/Heidelberg, 2000, ISBN 3-540-43580-8

1. ↑ Grimsehl: Lehrbuch der Physik, Bd. I; Leipzig 1954, S.579.

Siehe auch

• Gradient (Meteorologie)

Weblinks

• Druckgradient und Schallschnelle sind nicht das Gleiche (PDF; 144 kB)
• Wie "krümme" ich Nabla und Delta? – Herleitung des Nablaoperators für orthonormal krummlinige Koordinaten auf www.matheplanet.com