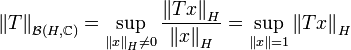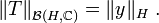- Darstellungssatz
-
Der rieszsche Darstellungssatz (nach Frigyes Riesz) charakterisiert in der Mathematik den Dualraum der Banachräume Lp, beziehungsweise in seiner Version auf C0(X) dem Dualraum der stetigen Funktionen auf einem lokalkompaktem Hausdorff-Raum. Er stellt die stetigen linearen Funktionale als Integral dar. Mit diesem Satz kann man schließlich das Lemma von Lax-Milgram beweisen, welches eine zufriedenstellende Existenztheorie für viele partielle Differentialgleichungen sichert.
Inhaltsverzeichnis
Aussage auf Lp
Sei zunächst zu
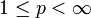 der konjugierte Exponent q mit
der konjugierte Exponent q mit 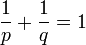 gegeben. Im Falle p = 1 wähle man
gegeben. Im Falle p = 1 wähle man 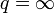 . Dann gibt es zu jedem stetigen linearen Funktional
. Dann gibt es zu jedem stetigen linearen Funktional 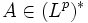 ein
ein 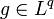 , so dass
, so dass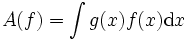 für alle
für alle 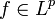
erfüllt ist.
Zum Beweis betrachtet man zunächst den Hilbertraumfall, also p=2, und beweist diese Aussage mit dem Projektionssatz. Den allgemeinen Fall führt man dann geschickt auf den soeben bewiesenen Spezialfall unter Anwendung eines Regularitätssatzes zurück.
Aussage auf C0(X)
X sei ein lokalkompakter Hausdorff-Raum und
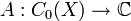 ein nicht-negatives, lineares Funktional. Dann existiert ein eindeutiges Radon-Maß μ auf X, so dass
ein nicht-negatives, lineares Funktional. Dann existiert ein eindeutiges Radon-Maß μ auf X, so dassA(f) = ∫ f(x)dμ(x) X für alle
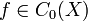 erfüllt ist.
erfüllt ist.Zum Beweis definiert man zunächst
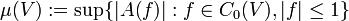 für alle offenen
für alle offenen 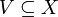
und
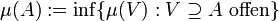 für alle
für alle 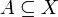 .
.
Anschließend wir nachgewiesen, dass dies ein Maß, dann dass es ein Radon-Maß ist.
Alternative Formulierung
Diese Formulierung ist allgemeiner und wird in der Fachliteratur als Darstellungssatz von Frechét-Riesz bezeichnet.
Sei H ein Hilbertraum mit Skalarprodukt
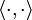 und induzierter Norm
und induzierter Norm 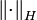 . Die Menge
. Die Menge 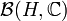 der linearen, stetigen (und also auch beschränkten) Funktionale über H wird mit der durch
der linearen, stetigen (und also auch beschränkten) Funktionale über H wird mit der durchdefinierten Norm zu einem Banachraum.
Dann gilt: Für jedes lineare und stetige Funktional
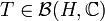 existiert ein eindeutiges
existiert ein eindeutiges 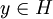 mit
mit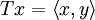 für alle
für alle 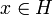
und
Konsequenzen
Neben dem oben erwähnten Lemma von Lax-Milgram folgt aus dem Satz auch noch die Existenz eines isometrischen Isomorphismus von (Lp) * nach Lq. Zweimalige Anwendung dieser Überlegung liefert schließlich die Reflexivität der Banachräume Lp für
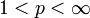 .
.Literatur
- Hans Wilhelm Alt: Lineare Funktionalanalysis. 5. Auflage. Springer, Berlin, Heidelberg, New York Juni 2006, ISBN 978-3-540-34186-4 (Dieses Buch ist eine schöne Einführung in dieses doch recht abstrakte Themengebiet. Besonderer Wert wird hier auf die Regularitätstheorie schwacher Lösungen partieller Differentialgleichungen gelegt.).
- Friedrich Sauvigny: Partielle Differentialgleichungen der Geometrie und der Physik. Band 1, Springer-Verlag, 2004 (Ein sehr ungewöhnliches Buch mit einer ausgeprägten Existenztheorie für klassische Lösungen und mit gut ausgearbeiteten Theorie über nicht-lineare Systeme in zwei Variablen. Hier ist auch der Beweis des Rieszschen Satzes im allgemeinen Fall zu finden.)
- Dirk Werner: Funktionalanalysis. Springer-Verlag, 2004 (Hier wird besonders viel Wert auf die Spektraltheorie auch unbeschränkter Operatoren gelegt. Die exakte Einführung der Distributionstheorie ist hier ebenfalls sehr gelungen.)
Wikimedia Foundation.