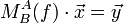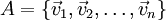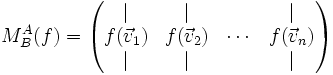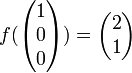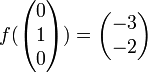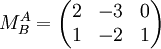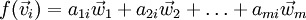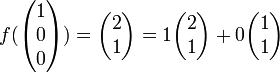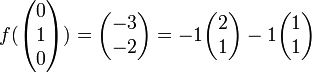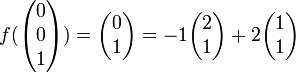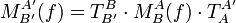- Darstellungsmatrix
-
Eine Abbildungsmatrix oder Darstellungsmatrix ist eine Matrix, die in der linearen Algebra verwendet wird, um eine lineare Abbildung zwischen zwei endlichdimensionalen Vektorräumen zu beschreiben.
Inhaltsverzeichnis
Verwendung von Abbildungsmatrizen
Voraussetzungen
Um eine lineare Abbildung von Vektorräumen durch eine Matrix beschreiben zu können, muss zunächst sowohl im Urbildraum als auch im Zielraum eine Basis (mit Reihenfolge der Basisvektoren) fest gewählt worden sein. Bei einem Wechsel der Basen in einem der betroffenen Räume muss die Matrix transformiert werden, sonst beschreibt sie eine andere lineare Abbildung!
Wenn in der Definitionsmenge und der Zielmenge eine Basis gewählt worden ist, dann lässt sich eine lineare Abbildung eindeutig durch eine Abbildungsmatrix beschreiben. Allerdings muss dafür festgelegt werden, ob man die Koordinaten von Vektoren in Spalten- oder Zeilenschreibweise notiert. Die üblichere Schreibweise ist die in Spalten.
Dazu muss man den Vektor, der abgebildet werden soll, als Spaltenvektor (bzgl. der gewählten Basis) schreiben.
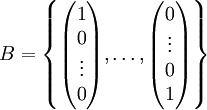
Aufbau der Abbildungsmatrix bei Verwendung von Spaltenvektoren
Nach der Wahl einer Basis aus der Definitionsmenge und der Zielmenge stehen in den Spalten der Abbildungsmatrix die Koordinaten der Bilder der Basisvektoren des abgebildeten Vektorraums bezüglich der Basis des Zielraums. Konkret: Der erste Basisvektor des Urbildraumes hat nach der Abbildung den Koordinatensatz aus der ersten Spalte usw. So wird die gesamte Abbildungsmatrix aufgebaut. Eine Abbildungsmatrix, die eine Abbildung aus einem 4-dimensionalen Vektorraum in einen 6-dimensionalen Vektorraum beschreibt, muss daher stets 6 Zeilen (für die sechs Bildkoordinaten der Basisvektoren) und 4 Spalten (für jeden Basisvektor des Urbildraums eine) haben.
Allgemeiner: Eine lineare Abbildungsmatrix
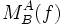 aus einem n-dimensionalen Vektorraum in einen m-dimensionalen Vektorraum hat m Zeilen und n Spalten. Das Bild eines Koordinatenvektors kann man dann so berechnen:
aus einem n-dimensionalen Vektorraum in einen m-dimensionalen Vektorraum hat m Zeilen und n Spalten. Das Bild eines Koordinatenvektors kann man dann so berechnen:Dabei ist
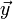 der Bildvektor,
der Bildvektor, 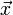 der Vektor, der abgebildet wird, jeweils in den Koordinaten ihres Raumes.
der Vektor, der abgebildet wird, jeweils in den Koordinaten ihres Raumes.Siehe hierzu auch: Aufbau der Abbildungsmatrix.
Verwendung von Zeilenvektoren
Verwendet man anstelle von Spalten- Zeilenvektoren, dann muss die Abbildungmatrix transponiert werden. Das bedeutet, dass nun die Koordinaten des Bildes des 1. Basisvektors im Urbildraum in der ersten Zeile stehen usw. Bei der Berechnung der Bildkoordinaten muss der (Zeilenkoordinaten-)vektor nun von links an die Abbildungsmatrix multipliziert werden.
Berechnung der Abbildungsmatrix
Abbildung in die Standardbasis
Sei
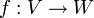 eine lineare Abbildung. Die Basis für V bezeichnen wir mit A:
eine lineare Abbildung. Die Basis für V bezeichnen wir mit A:Als Basis B für die Zielmenge W wählen wir die Standardbasis:
Die Abbildungsmatrix ergibt sich, indem man die Bilder der Basisvektoren von V als Spalten einer Matrix auffasst:
Beispiel: Sei
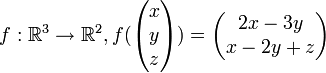 eine lineare Abbildung. Weiter sei
eine lineare Abbildung. Weiter sei 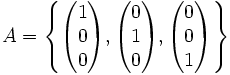 eine Basis des
eine Basis des  und
und 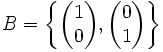 eine Basis des
eine Basis des 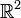 .
.Es gilt:
Damit ist die Abbildungsmatrix
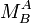 :
:Abbildung in eine allgemeine Basis
Ist die Basis der Zielmenge nicht die Standardbasis, sondern allgemein
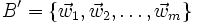 , so müssen die Bilder
, so müssen die Bilder  als Linearkombinationen der Basisvektoren von W dargestellt werden, um die Einträge aji der Abbildungsmatrix zu ermitteln:
als Linearkombinationen der Basisvektoren von W dargestellt werden, um die Einträge aji der Abbildungsmatrix zu ermitteln:Die Abbildungsmatrix ergibt sich dann, indem man die Koeffizienten der Linearkombinationen in die Matrix einträgt:
Beispiel: Wir nehmen wieder die lineare Abbildung f des obigen Beispiels. Diesmal bilden wir jedoch von der Basis A in die Basis
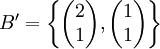 ab.
ab.Hier gilt nun:
Damit ist die Abbildungsmatrix
 :
:Basiswechsel
Ist die Abbildungsmatrix einer Abbildung für bestimmte Basen bekannt, so lässt sich die Abbildungsmatrix für dieselbe Abbildung, jedoch mit anderen Basen, leicht berechnen. Dieser Vorgang wird als Basiswechsel bezeichnet.
Die Abbildungsmatrix
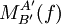 berechnet sich aus der Abbildungsmatrix
berechnet sich aus der Abbildungsmatrix 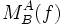 und den Basiswechselmatrizen
und den Basiswechselmatrizen 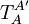 und
und 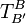 wie folgt:
wie folgt:Beschreibung von Endomorphismen durch Abbildungsmatrizen
Bei einer linearen Selbstabbildung (einem Endomorphismus) eines Vektorraums legt man gewöhnlich eine feste Basis des Vektorraumes als Definitionsmenge und Zielmenge zugrunde. Dann beschreibt die Abbildungsmatrix die Veränderung, die die Koordinaten eines beliebigen Vektors bezüglich dieser Basis bei der Abbildung erfahren. Die Abbildungsmatrix ist bei Endomorphismen stets quadratisch, d.h. die Zahl der Zeilen stimmt mit der Zahl der Spalten überein.
Beispiele für Abbildungsmatrizen
Im dreidimensionalen Raum (mit der kanonischen Basis) kann man die Projektion eines Vektors auf eine Ursprungsgerade durch folgende Abbildungsmatrix beschreiben:
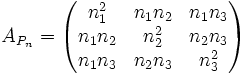 , dabei sind
, dabei sind 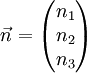 die Koordinaten des normierten Richtungsvektors der Geraden.
die Koordinaten des normierten Richtungsvektors der Geraden.Wird anstatt auf eine Gerade auf eine Ebene mit den beiden zueinander senkrechten, normierten Richtungsvektoren
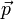 und
und 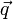 projiziert, so kann man dies in zwei Projektionen entlang der beiden Richtungsvektoren auffassen, und demnach die Projektionsmatrix für die Projektion auf eine Ursprungsebene folgendermaßen aufstellen:
projiziert, so kann man dies in zwei Projektionen entlang der beiden Richtungsvektoren auffassen, und demnach die Projektionsmatrix für die Projektion auf eine Ursprungsebene folgendermaßen aufstellen: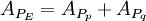
Die Projektionsmatrix um auf eine Ebene zu projizieren, ist also die Summe der Projektionsmatrizen auf ihre Richtungsvektoren.
Wird anstatt einer Projektion eine Spiegelung durchgeführt, so kann dies ebenfalls mit Hilfe der Projektionsmatrix dargestellt werden. Für die Spiegelung an einer Ursprungsgeraden mit normiertem Richtungsvektor
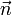 gilt:
gilt: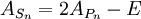 , wobei E die Einheitsmatrix darstellt.
, wobei E die Einheitsmatrix darstellt.Gleiches gilt für die Spiegelung an der Ebene:

Wenn man im dreidimensionalem Raum um eine Ursprungsgerade mit normiertem Richtungsvektor
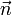 dreht, lässt sich die hierfür nötige Abbildungsmatrix ebenfalls folgendermaßen darstellen:
dreht, lässt sich die hierfür nötige Abbildungsmatrix ebenfalls folgendermaßen darstellen: , wobei E wieder die Einheitsmatrix, und α den Drehwinkel bezeichnet.
, wobei E wieder die Einheitsmatrix, und α den Drehwinkel bezeichnet.Siehe auch
Wikimedia Foundation.