- Dualer Operator
-
In der Funktionalanalysis kann zu jedem dicht definierten linearen Operator T ein adjungierter Operator (manchmal auch dualer Operator) T' definiert werden.
Lineare Operatoren können zwischen zwei Vektorräumen mit gemeinsamem Grundkörper K (
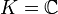 oder
oder 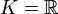 ) definiert werden, adjungierte Operatoren werden allerdings häufig nur auf Hilberträumen betrachtet, also beispielsweise (endlichdimensionalen) euklidischen Räumen. Auf endlichdimensionalen Räumen entspricht der adjungierte Operator der adjungierten Matrix. In der Matrizenrechnung mit reellen Einträgen entspricht die Bildung des adjungierten Operators dem Transponieren, bei komplexen Einträgen dem (komplex) Konjugieren und Transponieren der Ausgangsmatrix.
) definiert werden, adjungierte Operatoren werden allerdings häufig nur auf Hilberträumen betrachtet, also beispielsweise (endlichdimensionalen) euklidischen Räumen. Auf endlichdimensionalen Räumen entspricht der adjungierte Operator der adjungierten Matrix. In der Matrizenrechnung mit reellen Einträgen entspricht die Bildung des adjungierten Operators dem Transponieren, bei komplexen Einträgen dem (komplex) Konjugieren und Transponieren der Ausgangsmatrix.Inhaltsverzeichnis
Definition des adjungierten Operators
Seien X und Y Hilberträume. Die Operatoren
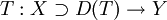 und
und 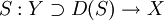 heißen formal zueinander adjungiert, falls
heißen formal zueinander adjungiert, falls 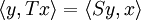 für alle
für alle 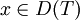 und
und 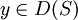 gilt. Unter diesen Voraussetzungen ist S im Allgemeinen nicht eindeutig durch T gegeben. Ist T dicht definiert, so existiert ein zu T maximaler formal adjungierter Operator T * . T * nennt man den adjungierten Operator von T.
gilt. Unter diesen Voraussetzungen ist S im Allgemeinen nicht eindeutig durch T gegeben. Ist T dicht definiert, so existiert ein zu T maximaler formal adjungierter Operator T * . T * nennt man den adjungierten Operator von T.Eigenschaften adjungierter Operatoren
Sei
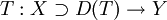 dicht definiert. Dann gilt:
dicht definiert. Dann gilt:- Ist D(T * ) dicht, so ist
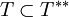 , d. h.
, d. h. 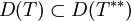 und T = T * * auf D(T)
und T = T * * auf D(T) 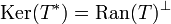
- T ist genau dann beschränkt, wenn T * beschränkt ist. In diesem Fall gilt
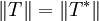
- Ist T beschränkt, so ist T * * die eindeutige Fortsetzung von T auf X
Sei
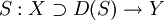 dicht definiert. Der Operator T + S ist definiert durch (T + S)x: = Tx + Sx für
dicht definiert. Der Operator T + S ist definiert durch (T + S)x: = Tx + Sx für 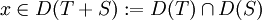 . Ist T + S dicht definiert, so ist
. Ist T + S dicht definiert, so ist 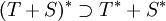 . Ist T beschränkt, so gilt sogar die Gleichheit.
. Ist T beschränkt, so gilt sogar die Gleichheit.Seien Z ein Hilbertraum und
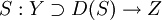 . Dann wird die Hintereinanderausführung bzw. Komposition TS von T und S definiert durch TSx: = T(Sx) für
. Dann wird die Hintereinanderausführung bzw. Komposition TS von T und S definiert durch TSx: = T(Sx) für 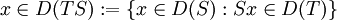 . Ist TS dicht definiert, so gilt
. Ist TS dicht definiert, so gilt 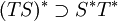 . Ist T beschränkt, erhält man (TS) * = S * T * .
. Ist T beschränkt, erhält man (TS) * = S * T * .Konstruktion für beschränkte Operatoren
Zur Vereinfachung kann der Bild- und Definitionsraum als gleich angenommen werden.
Beschränkte Operatoren können auf dem gesamten Hilbertraum X definiert werden. In diesem Fall ist für jedes
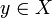 die Funktion
die Funktion 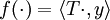 ein auf dem ganzen Hilbertraum definiertes, lineares stetiges Funktional, da aus der Beschränktheit des auf ganz X definierten linearen Operators T die Stetigkeit von f folgt.
ein auf dem ganzen Hilbertraum definiertes, lineares stetiges Funktional, da aus der Beschränktheit des auf ganz X definierten linearen Operators T die Stetigkeit von f folgt.Der Darstellungssatz von Riesz liefert für jedes stetige lineare Funktional f ein eindeutig bestimmtes Element
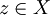 , sodass
, sodass 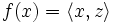 für alle
für alle  . Also existiert für jedes
. Also existiert für jedes 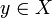 genau ein Element
genau ein Element 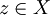 mit
mit 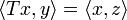 . Nun setzt man T * y: = z. Diese Konstruktion ist äquivalent zu obiger Definition.
. Nun setzt man T * y: = z. Diese Konstruktion ist äquivalent zu obiger Definition.Hermitesche, symmetrische und selbstadjungierte Operatoren; Entwicklungssatz
Ein Operator
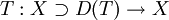 heißt
heißt- hermitesch, falls T zu sich selbst formal adjungiert ist
- symmetrisch, falls T hermitesch und dicht definiert ist
- selbstadjungiert, falls T dicht definiert und T = T *
Ist T beschränkt, so sind die Begriffe äquivalent. Bei nichtbeschränkten Operatoren impliziert zwar die Selbstadjungiertheit die Hermizität, aber die Umkehrung gilt nicht. Ein Gegenbeispiel gibt das folgende Paar:
- 1.) Der auf dem komplexen Hilbertraum
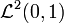 (generiert von den auf dem Intervall I = [0,1] quadratintegrierbaren komplexen Funktionen ψ(x)) definierte Operator, der durch den Differentialausdruck
(generiert von den auf dem Intervall I = [0,1] quadratintegrierbaren komplexen Funktionen ψ(x)) definierte Operator, der durch den Differentialausdruck 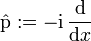 mit den „Dirichletschen Randbedingungen“
mit den „Dirichletschen Randbedingungen“ 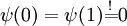 erzeugt wird.
erzeugt wird.
- 2.) Dessen Erweiterung, wo man nur „Periodizität“ fordert,
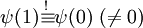 .
.
Aus der Identität
 erkennt man, dass zwar in beiden Fällen die Operatoren hermitesch sind, aber nur der zweite Operator selbstadjungiert ist, weil im ersten Fall der Definitionsbereich unnötig eingeengt wird. Schon auf den ersten Blick erkennt man den Unterschied ferner daran, dass im Fall 1.) der Operator gar keine Eigenfunktion besitzt, wogegen im Fall 2.) das System der Eigenfunktionen,
erkennt man, dass zwar in beiden Fällen die Operatoren hermitesch sind, aber nur der zweite Operator selbstadjungiert ist, weil im ersten Fall der Definitionsbereich unnötig eingeengt wird. Schon auf den ersten Blick erkennt man den Unterschied ferner daran, dass im Fall 1.) der Operator gar keine Eigenfunktion besitzt, wogegen im Fall 2.) das System der Eigenfunktionen, 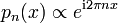 , mit
, mit 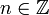 , sogar „vollständig“ ist (Fourieranalyse). Dies ist ein konkretes Beispiel für folgende Aussage: Jeder unbeschränkte hermitesche Operator im Hilbertraum kann zu einem selbstadjungierten erweitert werden.
, sogar „vollständig“ ist (Fourieranalyse). Dies ist ein konkretes Beispiel für folgende Aussage: Jeder unbeschränkte hermitesche Operator im Hilbertraum kann zu einem selbstadjungierten erweitert werden.Wichtiger ist der gleich anschließende Satz (er ist grundlegend für die Quantenmechanik):
- Ein selbstadjungierter Operator im Hilbertraum besitzt eine (vollständige) Spektralschar aus „eigentlichen“ bzw. „uneigentlichen“ Eigenfunktionen (Nebenbemerkung: die uneigentlichen Eigenfunktionen sind distributionswertig). Dies ist der sog. Entwicklungssatz.
Weitere Eigenschaften:
- Ist T ein dicht definierter Operator, dann ist T * T ein selbstadjungierter und positiver Operator.
Verallgemeinerung auf Banachräume
Adjungierte Operatoren können auch allgemeiner auf Banachräumen definiert werden. Für einen Banachraum X bezeichnet X' den topologischen Dualraum. Im Folgenden wird die Schreibweise
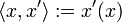 für
für  und
und 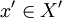 benutzt. Sind X,Y Banachräume, wird für einen dicht definierten Operator
benutzt. Sind X,Y Banachräume, wird für einen dicht definierten Operator 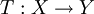 der adjungierte Operator durch
der adjungierte Operator durch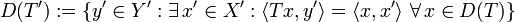
- T'y': = x' für
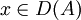
definiert.
Der Operator T' ist stets abgeschlossen, wobei D(T') = {0} möglich ist. Ist X ein reflexiver Banachraum und Y = X, dann ist T' genau dann dicht definiert, wenn T abschließbar ist. Insbesondere gilt dann
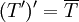 .
.Siehe auch
- Ist D(T * ) dicht, so ist
Wikimedia Foundation.
