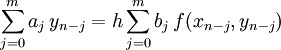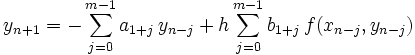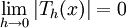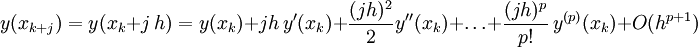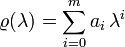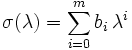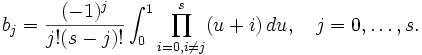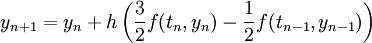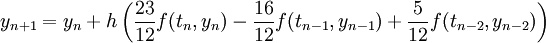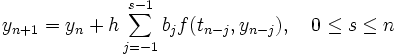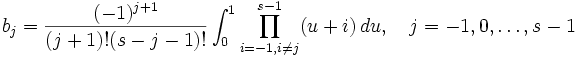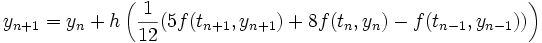Adams-Bashforth-Verfahren

Mehrschrittverfahren sind Verfahren zur numerischen Lösung von gewöhnlichen Differentialgleichungen. Im Gegensatz zu Einschrittverfahren, wie etwa dem Eulerschen Polygonzugverfahren oder den Runge-Kutta-Verfahren, nutzen Mehrschrittverfahren die Information aus den zuvor bereits errechneten Stützpunkten.

Theorie

Es sei ein Anfangswertproblem y'(x) = f(x,y(x)) für 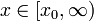$x\in [x_0,\infty)$ mit einer Anfangsbedingung y(x₀) = y₀ näherungsweise zu lösen. Ein lineares Mehrschrittverfahren (LMV) erzeugt zu einer gegebenen Schrittweite h>0 eine Folge 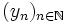$(y_n)_{n\in\N}$ von Näherungen zu den Funktionswerten $y_n\approx y(x_n)=y(x_0+n\,h)$.

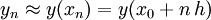Dabei besteht zwischen den Näherungswerten und der Differentialgleichung die lineare Rekursionsgleichung

$\sum_{j=0}^{m}a_{j} \, y_{n-j} = h \sum_{j=0}^m b_{j} \, f(x_{n-j},y_{n-j})$

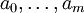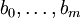Die Koeffizienten $a_0,\dots,a_m$ sowie $b_0,\dots,b_m$ bestimmen das Mehrschrittverfahren, dabei gilt a₀ = 1.

Man nennt das LMV implizit, falls 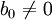$b_0 \neq 0$, und explizit, falls b₀ = 0. Implizite Verfahren können bei gleicher Länge m der Koeffiziententupel eine um 1 höhere Konsistenzordnung als explizite Verfahren haben. Ihr Nachteil besteht jedoch darin, dass bei der Berechnung von y_{n + 1} bereits f(x_{n + 1},y_{n + 1}) benötigt wird. Dies führt zu nichtlinearen Gleichungssystemen. Für explizite Verfahren kann man die lineare Rekursionsgleichung in die explizite Form

$y_{n+1}=-\sum_{j=0}^{m-1}a_{1+j} \, y_{n-j}+h \sum_{j=0}^{m-1} b_{1+j} \, f(x_{n-j},y_{n-j})$

umstellen.

In jedem Fall müssen die ersten m Glieder der Folge der Näherungswerte mit einem anderen Verfahren bestimmt werden, im einfachsten Fall wird linear extrapoliert,

$y_k=y_0+k\,h\,f(x_0,y_0)$, $k=1,\dots,m-1$.

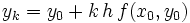Diese Werte können im Allgemeinen mit einem beliebigen Einschrittverfahren für den ersten Wert y₁, einem maximal 2-Schritt-Verfahren für den zweiten Wert y₂, usw. bis der m-1. Wert y_{m − 1} durch ein maximal m-1-Schritt-Verfahren gewonnen werden. Diese Berechnung nennt man auch Anlaufrechnung für das Mehrschrittverfahren.

Analyse

Man untersucht die LMV auf die Eigenschaften Konsistenz und Stabilität. Diese beiden Eigenschaften ergeben zusammen die Konvergenz des LMVs. Diese besagt, dass durch Verkleinern der Schrittweite h > 0 die Differenz | y_k − y(x_k) | zwischen Näherungswert und Wert der exakten Lösung für 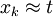$x_k\approx t$ für jedes fixierte t beliebig klein gehalten werden kann.

Konsistenz

Sei y(x) beliebige, in einer Umgebung eines Punktes x definierte und einmal stetig differenzierbare Funktion. Diese erfüllt die triviale Differentialgleichung y'(x) = f(x,y) = y'(x). Für diese kann der Fehler erster Ordnung des Mehrschrittverfahrens als

$T_h(x)=\frac{1}{h}\sum_{j=0}^{m}a_{j} \, y(x-j\,h) - \sum_{j=0}^m b_{j} \, y'(x-jh)$.

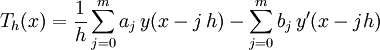bestimmt werden. Man definiert dann:

Ein LMV heißt konsistent, falls

$\lim_{h \to 0} |T_h(x)| = 0$

für beliebige Wahlen von x und der Funktion y. Es heißt konsistent der Ordnung p, falls in Landau-Notation

| T_h(x) | = O(h^p)

gilt, d. h. 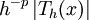$h^{-p}\,|T_h(x)|$ immer nach oben beschränkt ist.

Man prüft dies unter Zuhilfenahme der Taylor-Entwicklung. So ist für eine p-fach differenzierbare Differentialgleichung die Lösung p+1 mal differenzierbar und es gilt

$y(x_{k+j}) = y(x_k + j\, h) = y(x_k)+ jh \, y'(x_k)+ \frac{(jh)^2}{2}y''(x_k) + \dots + \frac{(jh)^p}{p!}\,y^{(p)}(x_k) + O(h^{p+1})$

wobei y^(l)(x_k) die l-te Ableitung an der Stelle x_k bezeichnet. Dies führt man für alle im LMV auftretenden Terme durch und setzt dies in T_h(x_k) ein. Es ist ausreichend, dies für die Exponentialfunktion und ihre Differentialgleichung zu untersuchen.

Stabilität

Man definiert zwei Polynome ρ,σ

$\varrho (\lambda) = \sum_{i=0}^ma_i \, \lambda^i$

$\sigma(\lambda) = \sum_{i=0}^mb_i \, \lambda^i$

Ein LMV wird durch diese beiden Polynome vollständig charakterisiert, so dass man anstelle von obiger Schreibweise des LMVs auch von einem „LMV (ρ,σ)“ spricht.

Sei λ₀ eine Nullstelle von ρ Ein LMV (ρ,σ) ist stabil, wenn für jede Nullstellen λ₀ gilt:

• sie liegt entweder im Innern des Einheitskreises, | λ₀ | < 1 oder
• auf dem Rand des Einheitskreises, | λ₀ | = 1, wobei sie dann eine einfache Nullstelle sein muss.

Beispiele

Explizite Verfahren

Ein explizites Verfahren bedeutet in diesem Zusammenhang, dass zur Berechnung der Näherungswerte nur Werte herangezogen werden, die zeitlich vor dem zu Berechnenden liegen. Das wohl bekannteste explizite LMV ist die s+1–Schritt Adams-Bashforth-Methode. Diese hat die Form:

$y_{n+1}=y_n + h \sum_{j=0}^s b_{j} \, f(t_{n-j},y_{n-j})$.

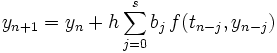mit

$b_j = {(-1)^j \over j!(s-j)!}\int_0^1 \prod_{i=0, i\ne j}^s (u+i) \,du,\quad j=0,\ldots, s.$

z. B.:

s = 1

$y_{n+1} = y_n + h\left( {3\over 2} f(t_n, y_n) - {1 \over 2} f(t_{n-1}, y_{n-1})\right)$

s = 2

$y_{n+1} = y_n + h\left( {23\over 12} f(t_n, y_n) - {16 \over 12} f(t_{n-1}, y_{n-1}) + {5\over 12}f(t_{n-2}, y_{n-2})\right)$

usw.

Implizite Verfahren

Bei impliziten Verfahren wird zur Berechnung auch der zu berechnende Wert selbst benutzt. Im Beispiel taucht so auf beiden Seiten der Gleichung y_{n + 1} auf. Das seinerseits bekannteste implizite LMV ist die Adams-Moulton-Methode. Dieses hat die Form:

$y_{n+1} = y_n + h \sum_{j=-1}^{s-1} b_j f(t_{n-j}, y_{n-j}),\quad 0 \le s \le n$

mit

$b_j = {(-1)^{j+1} \over (j+1)!(s-j-1)!}\int_0^1 \prod_{i=-1, i\ne j}^{s-1} (u+i) \,du,\quad j=-1,0,\ldots,s-1$

z. B.:

s = 2

$y_{n+1}=y_n+h\left({1 \over 12}(5f(t_{n+1}, y_{n+1})+8f(t_n,y_n)-f(t_{n-1},y_{n-1}))\right)$

Vorteile gegenüber Einschrittverfahren

Der offensichtliche Vorteil linearer Mehrschrittverfahren gegenüber Einschrittverfahren ist ihr Verhältnis zwischen Kosten und Konsistenzordnung. Dies liegt daran, dass bei einem LMV jeweils nur ein Wert aus bereits vorhandenem Datenmaterial berechnet werden muss.

Praxis

Startwerte

Oftmals hat man es in der Praxis mit Problemen der Art:

$y'(x)=f\left( x,y(x) \right) , \quad y(0)=y_0$

zu tun. Hier fehlt es an Startwerten. Diese werden zunächst durch Einschrittverfahren (z. B. dem klassischen Runge-Kutta-Verfahren) gewonnen.

Prädiktor-Korrektor-Methode

Mit dem Gedanken, die im Vergleich um 1 höhere Konsistenzordnung der impliziten LMVs zu nutzen, umgeht man das Lösen der nichtlinearen Gleichungen durch die sog. Prädiktor-Korrektor-Methode. Es wird der in der impliziten Methode benötigte Wert für y_{n + 1} durch eine explizite Methode berechnet, wonach durch Iteration der Wert für y_{n + 1} zu verbessern versucht wird. Dazu gibt es verschiedene Verfahren, die geläufigsten sind:

P(EC)^mE

Beim P(EC)^mE (P=predict, E=evaluate, C=correct) wird der durch das explizite Prädiktorverfahren gewonnene Wert y_{n + 1,alt} für y_{n + 1} wieder in das implizite Korrektorverfahren eingesetzt, wodurch man einen neuen Wert für y_{n + 1}, nämlich y_{n + 1,neu} erhält. Dies wird so lange iteriert, bis | y_{n + 1,neu} − y_{n + 1,alt} | kleiner als eine festgelegte Fehlertoleranz ist, oder m-mal iteriert wurde.