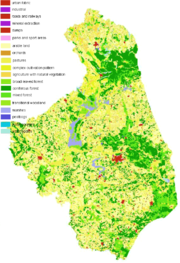
Dasymetrische Kartierung

Choroplethenkarte der Bevölkerungsdichte von Podlachien^[1]

Corin Land Cover von Podlachien^[2]

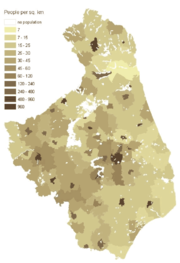Dasymetrische Karte von Podlachien (Binary Methode)^[3]

Von der Choroplethen- zur dasymetrischen Karte^[4]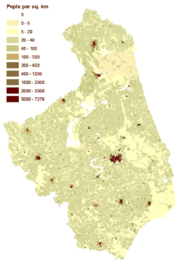

Dasymetrische Karte von Podlachien (Modifying Areal Weighting Methode)^[5]

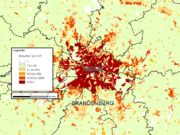Dasymetrische Karte von Berlin-Brandenburg^[6]

Dasymetrische Kartierung oder Darstellung, Dasymetrie, Dasymetric Mapping ist eine kartographische Ausdrucksform und Methode.

Definition

Dasymetrische Kartierung, bzw. Dasymetric Mapping ist eine Methode der thematischen Kartographie. Ihre Form entspricht der einer quantitative Karte, ähnlich einer Choroplethenkarte ^[7]. Inhaltliches Thema sind meist Populationsdarstellungen, hauptsächliche die Darstellung der Dichte. Besonders häufig ist sie in der Risikoanalyse und -kartierung zur Ermittlung der Anzahl der betroffenen Bevölkerung vorzufinden ^[8].

Nach Dent (1999)^[9] ist eine Charakteristik, die sie von der Choroplethenkarte abgrenzt, dass die statistische Oberfläche einer dasymetrischen Karte als Konstrukt aus Zonen mit einheitlichen Werten dargestellt wird, bei der die Abgrenzung der Zonen auf Basis der Wertunterschiede erfolgt. Diese Zonen sind getrennt durch Schwellen, die durch rapide Änderung der Werte definiert sind ^[10].

Obwohl etwas Ähnliches in Thematische Kartographie auf Seite 14 des ARNBERGER (1997)^[11] dargestellt wird, ist gerade im deutschsprachigen Raum die Darstellungsform des „Dasymetric Mapping“ nahe zu unbekannt. Das obwohl sie eine Vielzahl von Möglichkeiten offeriert, die die Choroplethenkarte nicht liefern kann.

Etymologie des Begriffs

Der Begriff Dasymetrie ist nicht sehr bekannt im deutschen Sprachraum. Das ist auch im Falle der „Dasymetrischen Darstellung“ kein Wunder. Den die Worte „Dasymetrie“ oder „dasymetrisch“ existiert in der deutschen Sprache nicht. Die einzige offizielle Verwendung in der deutschen Sprache ist das ähnlich klingende „Dasymeter“, der Luftwaage.

Tatsächlich aber wurde „Dasymetrie“ aus dem Englischen inoffiziell übertragen und bezieht sich auf „Dasymetric“ bzw. „Dasymetric Mapping“. „Dasymetric“ wiederum wurde abgeleitet von „dasýs“, griechisch für Dichte, lateinisch auch „dénsus“ und fand im Englischen seine Ausprägung als „density“. Somit kann man also sagen „Dasymetric Mapping“ ist zu übersetzen mit „Dichte messende Kartierung“.

Da „dasymetric“ auf „ic“ endet, lässt sich daraus schwer ein deutsches Adjektiv bilden. Z.B. würde „dasymeteric(al) Darstellung“ merkwürdig klingen. Daher wird für Vorgänge oder Beschreibungen das eingedeutschte „Dasymetrie“ oder „dasymetrisch“ verwendet, der Prozess als solches aber wird als „Dasymetric Mapping“ bezeichnet.

Ziel und Methodik

Das Ziel, ist die Modellierung einer genaueren räumlichen Verteilung von Populationen, als es bei der Choroplethenkarte möglich ist und deren Darstellung in Karten ^[12]. Genauer ist das Ziel, die Darstellung statistischer Oberflächendaten mittels größt möglicher Zerteilung der Fläche in Zonen deren Grenzen die darunterliegenden Unterscheide in der statistischen Oberfläche wiedergeben ^[13]. Stan Openshaw sagt zum Vergleich, dass die dasymetrische Methode eine quantitative Variable auf Grenzen, abgeleitet vom Charakter der Datenzusammensetzung, darstellt. Er nennt es eine Form der räumlichen Interpolation, die Zusatzdaten nutzt, um Populationsdaten von einem Satz räumlicher Einheiten in einen anderen zu transformieren ^[14]. Die Transformation vollzieht sich in Gestalt der Schaffung dasymetrischer Zonen. Diese entstehen durch das Verschneiden der Zonen der aggregierten Daten mit denen der unterstützenden Daten, z.B. der Landnutzung die ihrer Seits aus Zonen der verschieden Nutzungsklassen bestehen. Somit entstehen mehr und differenzierte Zonen, die eine Disaggregation der Daten erlauben, um selbst in Gebieten, in denen die Daten aggregiert aufgenommen wurden, eine genauere Darstellung als die der Ausgangsdaten zu ermöglichen. Eine dasymetrische Darstellung ist demnach ein Weg, diese Einschränkung der Genauigkeit zu vermeiden.

Durch den dasymetrischen Prozess werden die administrativen Einheiten in kleinere, mehr Karten relevante Einheiten, aufgespalten ^[15]. Das Wichtigste beim Dasymetric Mapping ist, laut Professor George F. McCleary, die Absicht und die Ausführung der Zusammenführung der Daten bei der Kartenherstellung durch den Kartographen. Des Weiteren schreibt er, es gäbe mehrere verschiedene Typen oder Formen der dasymetrischen Methode. McCleary hält 1969 die für die zweckmäßigste, die eine „innere Anpassung“ erfordert. Wenn man eine dasymetrische Oberfläche mittels der Methoden der innere Differenzierung entwickelt, sollte der Kartograph alle Elemente, die einen Einfluss auf das Muster der Zusammensetzung der dasymetrischen Zonen und auf die Schwellen der Variablen haben die er darstellen will, zum tragen bringen ^[16]. Das heißt der Kartograph definiert in der Karte Gebiete, mit denselben numerischen Werten, welche die dasymetrischen Zonen bilden. Die Zonen grenzen sich zueinander durch starke Gefälle der Werte ab. Die Methode benötigt intensive Arbeit bei der Produktion, viele Datenquellen und sorgfältig ausgewählte, im Zusammenhang stehende Vergleichs-karten und -daten.

Die dasymetrische Methode

Dieser Verschneidungsprozess weist den Zonen ihre disaggregierten Werte zu. Diese Zuweisung wird durch unterschiedliche, vom Kartographen bewusst gewählte mathematische Formeln, dasymetrische Methoden genannt, gesteuert.

Modifying Areal Weighting Methode

Der dasymetrische Prozess der veränderlichen Flächengewichtung wird Modifying Areal Weighting Methode genannt. Für diesen entwickelten Javier Gallego und Steve Peedell 2001 ^[17] den „Algorithmus von Gallego“. Dieser bedient sich einer iterativ ermittelten mittleren Populationsdichte für Landnutzungskategorien. Diese Landnutzungskategorien können z.B. durch Gruppieren von Landnutzungsklassen mit ähnlicher Populationsdichte erzeugt werden ^[18]. Errechnet wurde ein Ausgangskoeffizient für Landnutzungskategorien für Europa ^[19] Für jede Einheit kann iterativ ein Satz Gewichtungs-Populationskoeffizienten der Landnuntzungskategorien errechnet werden, bis die Differenz zum Indikator δ stabil geworden ist. Der Differenzindikator δ_r für ein Gebiet r ergibt sich aus der Summe der absoluten Werte der Differenz zwischen der zugeordneten 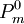$P_m^0$ und der statistisch bekannten Populationszahl P_m ^[20].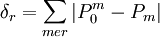

$\delta_r = \sum_{mer} |P_0^m-P_m|$

Um den Gewichtungs-Populationskoeffizienten in einer Einheit anzupassen, wird eine Korrelation ρ_cr zwischen dem Verhältnis von P_m^0 zu P_m und dem der Fläche der Landnutzungskategorie in der Einheit (A_cm) zur Gesamtfläche der Einheit (A_m) berechnet ^[21]. ρ_cr=corr((P_m^0)/P_m ,A_cm/A_m ) Diese Korrelation kann anschließend verwendet werden um eine neues U_c zu berechnen. U_cr^'=U_c (1-(ρ_cr×δ_r)/(2× P_r ))

Binary Methode

Die Binary Methode bzw. der binäre dasymetrische Prozess wurde besonders von Langford und Unwinn 1994^[22] und Eicher und Brewer 2001 ^[23] beschrieben. Die Individuendichte wird berechnet durch die Teilung der Anzahl der Individuen in einer Zähleinheit, durch die Fläche des bewohnten Teils. In Ab-bildung 2.2 kommt diese Methode bildhaft zum tragen. Der Hauptvorteil dieser Methode ist seine Einfachheit. Es ist nur nötig Landnutzungsdaten in bewohnte und unbewohnte Flächen einzuteilen. Der Nachteil ist die Subjektivität der Reklassifikation, der Einfluss der Größe der kleinsten dargestellten Einheit und anderen Zusatzinformationen über das Gebiet ^[24].

Intelligent Dasymetric Mapping

Diese Methode, auch IDM genannt, die besonders von Jeremy Mennis und Torin Hultren erforscht wird, beschäftigt sich mit dem Charakter der Beziehung zwischen Zusatzdaten und der erzeugten statistischen Oberfläche. Sie wird „intelligent“ genannt, da sie die Beziehungen herstellt die der Analyst sonst subjektiv durch sein Wissen herstellt. IDM stellt diese mit Hilfe von empirischer Sampling-Technologie her oder verbindet subjektive mit empirischen Methoden ^[25]. Die „intelligente“ Methode verbindet das Wissen des Analysten mit einer datenbasierten Methodologie, um den funktionalen Zusammenhang zwischen den Klassen der Zusatzda-ten und der statistischen Oberfläche die dargestellt wird zu spezifizieren. Die datenbasierte Komponente sammelt empirisch Informationen über die Datendichte der einzelnen Klassen der Zusatzdaten und nutzt das Verhältnis der Klassendichte zur Neuverteilung der Population auf Unter-Quell-Zonenflächen ^[26].

Literatur

• Bielecka, Elzbieta (2004): A Dasymetric population density map of Poland. Institut der Geodäsie und Kartographie, Warschau.
• Braumann, Birgit (2006): Objektorientierte Gebäudedetektion in Laserscannerdaten und multispektralen Bildern. Diplomarbeit am Institut für Photogrammetrie und Fernerkundung der TU Wien, S.25.
• Dent, Borden D. (1999): Cartography: Thematic Map Design. 5. Auflage, McGraw-Hill Publishing
• Chen, Keping et al. (2004): Defining area at risk and its effect in catastrophe loss estimation a dasymetric mapping approach. Applied Geography 24, S.101.
• Eicher, Corey L.; Brewer, Cynthia A. (2001): Dasymetric mapping and areal interpolation: implementation and evaluation. Cartography and Geographic Information Science 28, S.125-38.
• Gallego, Javier; Peedell, Steve (2001): Using CORINE Land cover to map population density. Towards agrienvironmental indicators. EEA Topic report 6, S.94-105.
• Langford, Mitchel; Unwin, David J. (1994): Generating and mapping population density surface within a geographical information system. The Cartographic Journal 31, S.21-26.
• McCleary, George F. Jr. (1969): The Dasymetric Method in Thematic Cartography. Unveröffentlichte Dissertation, Universität von Wisconsin.
• Openshaw, Stan (1983): The modifiable areal unit problem. Concepts and Techniques in Modern Geography vol. 38.
• Schulte, Bennet (2008): Dasymetrische Modellierung der Verteilung von Populationen. Technische Fachhochschule Berlin.
• Thieken et al. (2006): Risikokarten für Deutschland: erste Ergebnisse vom CEDIM. Zweijahresbericht 2004/2005, GeoForschungsZentrum Potsdam, S.141-152.
• Thieken, Annegret (2007): Risikokartierung. GS Magazin Nr.165, S.50.
• Mennis, Jeremy; Hultren, Torrin (2006): Intelligent Dasymetric Mapping and Its Application to Areal Interpolation. Cartography and Geographic Information Science, Volume 33, Nr. 3, Juli 2006, S.179-194.
• Mennis, Jeremy; Hultren, Torrin (2008): Dasymetric Mapping and Areal Interpolation. – Online in Internet: http://astro.temple.edu/~jmennis/research/dasymetric/index.htm [Stand 27.03.2008]

Einzelnachweise

1. ↑ Bielecka, Elzbieta (2004): A Dasymetric population density map of Poland. Institut der Geodäsie und Kartographie, Warschau.
2. ↑ Bielecka, Elzbieta (2004): A Dasymetric population density map of Poland. Institut der Geodäsie und Kartographie, Warschau.
3. ↑ Bielecka, Elzbieta (2004): A Dasymetric population density map of Poland. Institut der Geodäsie und Kartographie, Warschau.
4. ↑ Thieken, Annegret (2007): Risikokartierung. GS Magazin Nr.165, S.50.
5. ↑ Bielecka, Elzbieta (2004): A Dasymetric population density map of Poland. Institut der Geodäsie und Kartographie, Warschau.
6. ↑ Schulte, Bennet (2008): Dasymetrische Modellierung der Verteilung von Populationen. Technische Fachhochschule Berlin.
7. ↑ Dent, Borden D. (1999): Cartography: Thematic Map Design. 5. Auflage, McGraw-Hill Publishing
8. ↑ Thieken, Annegret (2007): Risikokartierung. GS Magazin Nr.165, S.50.
9. ↑ Dent, Borden D. (1999): Cartography: Thematic Map Design. 5. Auflage, McGraw-Hill Publishing
10. ↑ McCleary, George F. Jr. (1969): The Dasymetric Method in Thematic Cartography. Unveröffentlichte Dissertation, Universität von Wisconsin.
11. ↑ Arnberger, Erik (1997): Thematische Kartographie. 4. Auflage, Westermann, Braunschweig, S.16.
12. ↑ Thieken, Annegret (2007): Risikokartierung. GS Magazin Nr.165, S.50.
13. ↑ Mennis, Jeremy; Hultren, Torrin (2006): Intelligent Dasymetric Mapping and Its Application to Areal Interpolation. Cartography and Geographic Information Science, Volume 33, Nr. 3, Juli 2006, S.179-194.
14. ↑ Openshaw, Stan (1983): The modifiable areal unit problem. Concepts and Techniques in Modern Geography vol. 38.
15. ↑ Openshaw, Stan (1983): The modifiable areal unit problem. Concepts and Techniques in Modern Geography vol. 38.
16. ↑ McCleary, George F. Jr. (1969): The Dasymetric Method in Thematic Cartography. Unveröffentlichte Dissertation, Universität von Wisconsin.
17. ↑ Gallego, Javier; Peedell, Steve (2001): Using CORINE Land cover to map population density.
18. ↑ Bielecka, Elzbieta (2004): A Dasymetric population density map of Poland. Institut der Geodäsie und Kartographie, Warschau.
19. ↑ Gallego, Javier; Peedell, Steve (2001): Using CORINE Land cover to map population density.
20. ↑ Bielecka, Elzbieta (2004): A Dasymetric population density map of Poland. Institut der Geodäsie und Kartographie, Warschau.
21. ↑ Bielecka, Elzbieta (2004): A Dasymetric population density map of Poland. Institut der Geodäsie und Kartographie, Warschau.
22. ↑ Langford, Mitchel; Unwin, David J. (1994): Generating and mapping population density surface within a geographical information system. The Cartographic Journal 31, S.21-26.
23. ↑ Eicher, Corey L.; Brewer, Cynthia A. (2001): Dasymetric mapping and areal interpolation: implementation and evaluation. Cartography and Geographic Information Science 28, S.125-38.
24. ↑ Bielecka, Elzbieta (2004): A Dasymetric population density map of Poland. Institut der Geodäsie und Kartographie, Warschau.
25. ↑ Mennis, Jeremy; Hultren, Torrin (2006): Intelligent Dasymetric Mapping and Its Application to Areal Interpolation. Cartography and Geographic Information Science, Volume 33, Nr. 3, Juli 2006, S.179-194.
26. ↑ Mennis, Jeremy; Hultren, Torrin (2006): Intelligent Dasymetric Mapping and Its Application to Areal Interpolation. Cartography and Geographic Information Science, Volume 33, Nr. 3, Juli 2006, S.179-194.

Weblinks

• Dasymetric Mapping and Areal Interpolation (englisch)
• Semesterarbeit an der TFH Berlin (deutsch)