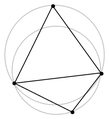
Delaunay-Triangulation

Die Delaunay-Triangulation ist ein gebräuchliches Verfahren, um aus einer Punktemenge ein Dreiecksnetz zu erstellen. Sie ist nach dem russischen Mathematiker Boris Nikolajewitsch Delone (1890–1980, franz. Form des Nachnamens: Delaunay) benannt, welcher sich 1934 in einer Veröffentlichung damit auseinandergesetzt hat.^[1]

Anwendung

Mit dem Verfahren der Delaunay-Triangulation werden Punkte im $\mathbb{R}^2$ so zu Dreiecken vernetzt, dass innerhalb des Kreises, auf dem die drei Dreieckspunkte liegen, keine anderen Punkte enthalten sind. Man verwendet das Verfahren zum Beispiel zur Optimierung von Berechnungsnetzen für die Finite-Elemente-Methode.

Prinzip

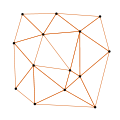
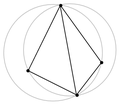
In einer Delaunay-Triangulation erfüllen alle Dreiecke des Dreiecksnetzes die sogenannte Umkreisbedingung: Der Umkreis eines Dreiecks des Netzes darf keine weiteren Punkte der vorgegebenen Punktmenge enthalten. Dadurch weisen die Dreiecke des Netzes möglichst große Innenwinkel auf; mathematisch gesprochen wird „der kleinste Innenwinkel über alle Dreiecke maximiert“. Diese Eigenschaft ist in der Computergrafik sehr erwünscht, denn sie minimiert Rundungsfehler.

Die Delaunay-Triangulation ist nicht eindeutig, falls auf einem Umkreis mehr als drei Punkte liegen, d. h. der Anwender kann sich beliebig aussuchen, welche drei Punkte er zu einem Dreieck verbindet.

Im dreidimensionalen Raum wird statt der Umkreisbedingung die analoge Umkugelbedingung verwendet, welche dann aus jeweils vier Punkten einen Tetraeder erzeugt.

Zusammenhang mit Voronoi-Diagrammen

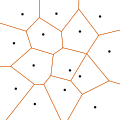
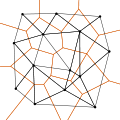
Die Delaunay-Triangulierung ist der duale Graph des Voronoi-Diagramms der Punktemenge: Die Ecken der Voronoizellen sind die Umkreismittelpunkte der Dreiecke der Delaunay-Triangulation (man erhält die Voronoi-Zellen, wenn man von allen Dreieckseiten die Mittelsenkrechten bis zum gemeinsamen Schnittpunkt mit den anderen beiden Mittelsenkrechten desselben Dreiecks einzeichnet; dieser Punkt kann, bei stumpfwinkligen Dreiecken durchaus außerhalb der Dreiecksfläche liegen, bei rechtwinkligen Dreiecken ist es der Punkt, der die Hypotenuse halbiert).

• 

  Delaunay-Triangulation einer Menge von Punkten in der Ebene.

• 

  Voronoi-Diagramm der gleichen Menge von Punkten.

• 

  Voronoi-Diagramm (orange) und Delaunay-Triangulation (schwarz)

Algorithmen

Es gibt mehrere Ansätze, um eine Delaunay-Triangulation durchzuführen^[2]. Die beste erreichte Laufzeit liegt bei $\mathcal{O}(n\,\log\,n)$ bei einem Speicherplatzbedarf von $\mathcal{O}(n)$.

Flip

Der Flip-Algorithmus ist eine spezielle Ausprägung für zweidimensionale Dreiecksnetze. Er basiert auf einer lokalen Auswertung der Umkreisbedingung.

Zunächst wird mit einem einfachen Algorithmus ein beliebiges Dreiecksnetz erzeugt. Dieses muss keineswegs die Umkreisbedingung erfüllen, es darf lediglich keine sich überschneidenden Kanten enthalten.

Für jedes Dreieck wird geprüft, ob der Umkreis dieses Dreiecks einen weiteren Punkt einschließt, der Teil eines angrenzenden Dreiecks ist. In diesem Fall wird ein Flip der gemeinsamen Kante durchgeführt. Das heißt, die gemeinsame Kante wird durch eine neue Kante ersetzt, die die beiden Punkte verbindet, die vorher nicht verbunden waren. Nach dem Flip ist die Umkreisbedingung lokal erfüllt. Allerdings kann dadurch die Umkreisbedingung in den benachbarten Dreiecken wieder gestört worden sein. Im schlechtesten Fall müssten also nach einem Flip alle anderen Dreiecke wieder überprüft werden, weshalb der Rechenaufwand des Flip-Algorithmus $\mathcal{O}(n^2)$ ist.

• 

  Diese beiden Dreiecke erfüllen die Umkreisbedingung nicht.

• 

  Nach dem Flip ist die Umkreisbedingung (lokal) erfüllt.

Incremental Construction (Inkrementelle Konstruktion)

Bei der Inkrementellen Methode^[3] werden die Punkte einer nach dem anderen hinzugefügt. Im Gegensatz zu den anderen Verfahren lässt sich so nicht nur die Delaunay-Triangulation einer festen Punktemenge erzeugen, sondern auch später noch durch Punkte erweitern, die zu Anfang noch nicht bekannt waren und erst durch einen Prozess bestimmt werden. Der Kern dieser Methode ist ein Algorithmus, der eine bestehende Delaunay-Triangulation voraussetzt und innerhalb dieser einen Punkt hinzufügt. Als Initialisierung genügt es, ein Dreieck vorzugeben, welches das Gebiet aller zu erwartenden Punkte einschließt. Der Algorithmus lässt sich in drei Schritte unterteilen:

• In der Triangulation wird jenes Dreieck gesucht, welches den neuen Punkt enthält. Eine naive Methode, einfach jedes Dreieck zu testen, hat den Aufwand $\mathcal{O}(n)$.
• Der neue Punkt wird mit den drei Ecken des gefundenen Dreiecks verbunden, sodass drei neue Dreiecke entstehen. Diese Triangulation erfüllt nun möglicherweise nicht mehr die Delaunay-Bedingung.
• Jedes der drei neuen Dreiecke wird dann auf die Umkreisbedingung getestet und gegebenenfalls wie im Flip-Algorithmus korrigiert. Nach jeder Korrektur gibt es weitere Dreiecke, die möglicherweise nicht mehr die Umkreisbedingung erfüllen. Dieses Testen und Korrigieren setzt sich durch die Triangulation fort, bis alle Dreiecke die Umkreisbedingung erfüllen. Da im schlechtesten Fall alle Dreiecke korrigiert werden müssen, ist der Aufwand theoretisch $\mathcal{O}(n)$. Dieser Fall wird aber selten auftreten. Werden die Punkte in zufälliger Reihenfolge eingefügt, müssen meist nur eine begrenzte Zahl von Korrekturen durchgeführt werden, sodass ein durchschnittlicher Aufwand von $\mathcal{O}(1)$ zu erwarten ist^[4].

Die Suchmethode mit $\mathcal{O}(n)$ für alle n Punkte durchzuführen, hat den Aufwand $\mathcal{O}(n^2)$. Die Korrekturen für n Punkte (bei zufälliger Reihenfolge) nur $\mathcal{O}(n)$. Der Gesamtaufwand ist daher durch die Suche bestimmt. Eine einfache Möglichkeit zur Verbesserung der Suche ist, die Triangulation von einem beliebigen Dreieck ausgehend in Richtung des gesuchten Punktes zu durchlaufen. Der Aufwand dieser Methode ist $\mathcal{O}(\sqrt{n})$. Eine etwas kompliziertere Suche lässt sich implementieren, wenn man die Geschichte aller erzeugten Dreiecke in einem Baum speichert. Diese Baumstruktur benötigt zwar zusätzlichen Speicherplatz, verbessert aber die Suche und damit den gesamten Inkrementellen Algorithmus auf $\mathcal{O}(n\log{n})$^[4].

Divide and conquer

Der Teile-und-herrsche-Ansatz verbindet jeweils zwei Delaunay-Triangulationen unter Einhaltung der Delaunay-Bedingung. Der Rechenaufwand liegt bei $\mathcal{O}(n\,\log\,n)$ ^[2].

Sweep

Der Sweep-Algorithmus fügt immer ein Dreieck unter Einhaltung der Delaunay-Bedingung hinzu. Im Gegensatz zur inkrementellen Konstruktion wird hier stets ein benachbartes Dreieck angefügt, während bei der inkrementellen Konstruktion ein beliebiges Dreieck angefügt werden kann. Der Rechenaufwand liegt bei $\mathcal{O}(n\,\log\,n)$ ^[2].

Voronoi

Beim Voronoi-Ansatz wird zunächst der Voronoi-Graph für alle Punkte gebildet. Durch die Dualität zum Dreiecksnetz hat man so bereits alle nötigen Umkreismittelpunkte bestimmt und muss nun nur noch die dazugehörigen Kreise ziehen.

Berechnung über die konvexe Hülle in 3D

Jeder 2D-Punkt wird um eine z-Koordinate mit z = x² + y² erweitert. Um diese 3D-Punkte wird die konvexe Hülle – eine mit Dreiecken facettierte Oberfläche – erstellt. Die Orientierung der Dreiecksnormalen sei nach außen festgelegt. Werden alle nach unten orientierten Dreiecke (also jene mit negativer z-Koordinate ihres Normalenvektors) in die ursprüngliche xy-Ebene zurückprojiziert, erhält man dort das gesuchte 2D-Delaunay-Dreiecksnetz. Der Zeitaufwand liegt in $\mathcal{O}(n\,\log\,n)$^[5].

Literatur

• R. Klein: Algorithmische Geometrie. Springer (2005)
• F. Aurenhammer und R. Klein: Voronoi Diagrams
• A. Okabe, et. al.: Spatial Tessellations: Concepts and Applications of Voronoi Diagrams. Wiley (2000)

Referenzen

1. ↑ Delaunay, Boris N.: Sur la sphère vide. In: Bulletin of Academy of Sciences of the USSR 7 (1934), Nr. 6, S. 793-800
2. ↑ ^{a b c} Lehner, Tomas: Digitale Geländemodellierung mittels Delaunay-Triangulierung und Abbauplanung in AutoCAD. Linz, Johannes Kepler Universität, Institut für Technische Informatik und Telematik, Dipl.-Arb., 2002, S. 15-20
3. ↑ F. Aurenhammer und R. Klein: Voronoi Diagrams
4. ↑ ^{a b} P. Su and R.L.S. Drysdale: A Comparison of Sequential Delaunay Triangulation Algorithms. 1996
5. ↑ Klein, Rolf: Algorithmische Geometrie. Springer, 2005, S. 304ff

Weblinks

 Commons: Delaunay triangulation – Sammlung von Bildern, Videos und Audiodateien

• Applet zur Berechnung und Visualisierung der konvexen Hülle, Delaunay-Triangulation und des Voronoi-Diagramms im Raum
• Java Applet für Delaunay-Triangulation - Fern Uni Hagen
• Java Applet für Delaunay-Triangulation
• Weiteres Java-Applet
• Weiteres Java-Applet
• Triangle - Ein Programm zur Generierung von 2D Delaunay-Triangulierungen
• WMG - Eine Web-Applikation zur numerischen 2D Delaunay-Gittergenerierung
• 2D Delaunay-Triangulation in C#