Voronoi-Diagramm

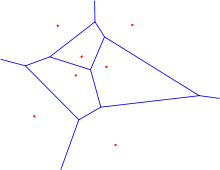
Als Voronoi-Diagramm, auch Thiessen-Polygonen oder Dirichlet-Zerlegung, wird eine Zerlegung des Raumes in Regionen bezeichnet, die durch eine vorgegebene Menge an Punkten des Raumes, hier als Zentren bezeichnet, bestimmt werden. Jede Region wird durch genau ein Zentrum bestimmt und umfasst alle Punkte des Raumes, die in Bezug zur euklidischen Metrik näher an dem Zentrum der Region liegen, als an jedem anderen Zentrum. Derartige Regionen werden auch als Voronoi-Regionen bezeichnet. Aus allen Punkten, die mehr als ein nächstgelegenes Zentrum besitzen und somit die Grenzen der Regionen bilden, entsteht das Voronoi-Diagramm.

Benannt sind Voronoi-Diagramme nach dem Mathematiker Georgi Feodosjewitsch Woronoi, die alternativen Bezeichnungen leiten sich von Alfred H. Thiessen respektive Peter Gustav Lejeune Dirichlet ab.

Beispiel einer Dirichlet-Zerlegung zu einer vorgegebenen Menge an Punkten.

Allgemeines

Voronoi-Diagramme werden in verschiedensten wissenschaftlichen Bereichen wie der Biologie, Chemie, Meteorologie, Kristallographie und anderen wissenschaftlichen Disziplinen wie der Algorithmischen Geometrie und der Materialwissenschaft verwendet. Ein Spezialfall des Voronoi-Diagramms im dreidimensionalen Raum ist die Wigner-Seitz-Zelle. Obwohl 1644 schon durch Descartes in seinem Buch Principia Philosophiae erwähnt, erfuhren sie erstmals durch Dirichlet und Voronoi eine genauere mathematische Analyse.^[1] Voronoi-Diagramme können durchaus auch als Zerlegung hochdimensionaler Räume verwendet werden. In der Literatur ist die Definition meist auf den zweidimensionalen reellen Raum beschränkt.

Definition

Die Thiessen-Polygone oder das Voronoi-Diagramm besteht aus dem gesamten Raum abzüglich der Voronoi-Regionen, welche in Bezug auf den euklidischen Abstand aus allen Punkten des Raumes entstehen, die näher am korrespondierenden Zentrum liegen als an allen anderen Zentren. Diese können im Zweidimensionalen als Schnitt mehrerer offener Halbebenen betrachtet werden, welche wiederum durch einen Bisektor zwischen je zwei Punkten der Zentren begrenzt werden.

Formal ist eine Voronoi-Region VR(p,S) des Punktes $p \in S$, wobei S eine vorgegebene Menge an Punkten des $\mathbb{R}^2$ ist, gegeben durch

$VR(p, S)=\bigcap_{q \in S \setminus \{p\}}D(p,q)$,

wobei D(p,q) als offene Halbebene definiert ist und durch

$D(p,q)=\{x \in \mathbb{R}^2:|p-x|<|q-x|\}$

gegeben ist. Sind nun alle Voronoi-Regionen durch

$VR(S)=\bigcup_{p \in S}VR(p,S)$

gegeben, erhält man das Voronoi-Diagramm durch

$V(S)=\mathbb{R}^2 \setminus VR(S)$

Informell bedeutet das, dass genau die Grenzen der Regionen, welche selbst nicht zu diesen dazu gehören, das Diagramm bzw. die Polygone bilden. Die resultierenden Polygone können in Voronoi-Kanten (Kanten des Polygons) und Voronoi-Knoten (Ecken des Polygons) eingeteilt werden. Alle Punkte auf den Voronoi-Kanten haben dabei zu den Punkten $p \in S$, deren Voronoi-Region neben der Kante liegen, den gleichen Abstand.

Erstellung des dualen Graphen eines Thiessen-Polygons

Dualität

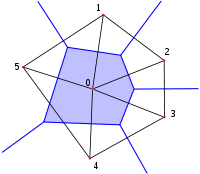
Das Voronoi-Diagramm verhält sich dual zur Delaunay-Triangulation und wird zur Konstruktion einer entsprechend triangulierten Oberfläche verwendet.

Um die Delaunay-Triangulation zu berechnen, wird der entsprechende duale Graph zum Voronoi-Diagramm gebildet. Dies geschieht, indem die Zentren der Polygone derart miteinander verbunden werden, so dass zu jeder Voronoi-Kante eine orthogonale Linie eingezeichnet wird, die die entsprechenden zwei Zentren miteinander verbindet (siehe Abbildung).

Polygon-Methode

Thiessen-Polygone werden unter anderem bei der kartographischen Darstellung von Messwerten eingesetzt. Die Polygon-Methode ist ein nichtstatistisches (d.h. vergleichsweise einfaches) Interpolationsverfahren der Geostatistik zur einfachen Darstellung der räumlichen Verteilung georeferenzierter Messdaten.

Als Grundannahme gilt, dass die Ähnlichkeit des unbekannten Wertes eines Punktes in der Fläche zum bekannten Messwert mit der Entfernung von diesem abnimmt, die Daten also umso unähnlicher sind, je weiter sie auseinander liegen. Dieser Zusammenhang wird bei der Polygon-Methode dadurch zum Ausdruck gebracht, dass jeder Messwert für ein ihn umgebendes Thiessen-Polygon homogenisiert wird, also alle Schätzwerte innerhalb dieses Polygons identisch zum jeweiligen Messwert sind.

Das Verfahren bildet insofern eine schlechte Näherung an die beobachtbare Realität, da an den Polygongrenzen scharfe Wertesprünge auftreten; fließende Übergänge zwischen zwei Messwerten können mit dieser Methode also nicht dargestellt werden. Durch diesen Umstand ist die Polygon-Methode wiederum gut geeignet zur flächigen Verteilung von diskreten Daten, etwa binären (z.B. Messwert: "Schneefall: ja/nein").

Algorithmus

Eingefärbtes Voronoi-Diagramm mit zufällig verteilten Punkten in der Ebene

Die Berechnung eines Voronoi-Diagramms mithilfe der Delaunay-Triangulation ist für beliebige Dimensionen möglich. Im Folgenden wird ein Algorithmus für den zweidimensionalen Fall beschrieben, der sich analog auf höhere Dimensionen erweitern lässt. Die Berechnung erfolgt in drei Schritten. Zunächst werden alle gegebenen Punkte in der x,y-Ebene in eine zusätzliche Dimension z auf ein (Hyper-)Paraboloid (x,y,x² + y²) projiziert. Von den so gewonnenen Punkten wird die Konvexe Hülle berechnet. In einem zweiten Schritt werden alle Flächen der Konvexen Hülle, deren Flächennormalen nach unten zeigen, wieder auf die ursprüngliche Ebene zurückprojiziert. Die so gewonnenen Regionen sind die Dreiecke der Delaunay-Triangulation. In einem letzten Schritt werden die Umkreismittelpunkte aller Dreiecke zwischen angrenzenden Dreiecken verbunden, was die gesuchten Kanten der Voronoi-Polygone ergibt.

In drei Dimensionen sind entsprechend die Kugelmittelpunkte durch Ecken der Delaunay-Tetraeder mit Flächen zu verbinden.

Pseudocode

Bezeichnungen: Punkte P, Delaunay-Triangulation DT(P), Konvexe Hülle KH(P), Voronoi-Diagramm V(P).

 1: Initialisiere leere Mengen P', DT(P) und V(P)
 2:
 3: //Berechnung der konvexen Hülle
 4: Für alle p = (px, py) $\in$ P:
 5:    Füge p' = (px, py, px2 + py2) zu P' hinzu
 6: Berechne KH(P') //Mit geeignetem Algorithmus
 7:
 8: //Berechnung der Delaunay-Triangulation
 9: Für alle Seiten s $\in$ KH(P'):
10:    Falls Normalenvektor von s nach unten zeigt:
11:       Für alle Kanten k von s:
12:          Setze z-Wert von jedem Knoten $\in$ k auf 0
13:          Erstelle neue Kante k' = k
14:          Füge k' zu DT(P) hinzu
15:
16: //Berechnung der Voronoi-Zellen
17: Für alle Dreiecke d in DT(P):
18:    Für alle an d angrenzenden Dreiecke d':
19:       Erstelle Kante m durch Verbindung der Umkreismittelpunkte von k und k'
20:       Füge m zu V(P) hinzu

Nach ^[2].

Literatur

• Atsuyuki Okabe, Barry Boots, Kokichi Sugihara, Sung Nok Chiu (Hrsg.): Spatial Tessallations: Concepts and Applications of Voronoi Diagrams. 2. Auflage. John Wiley & Sons, 2000, ISBN 978-0-47-198635-5.

Weblinks

•  Commons: Voronoi diagrams – Sammlung von Bildern, Videos und Audiodateien
• MathWorld (englisch)
• Java-Applet für Voronoi-Diagramme
• Weiteres Java-Applet
• Zelluläre Raumstruktur, mit Hilfe von Voronoi generiert (englisch)
• Java-Applet, das die Konstruktion eines Voronoi-Diagramms im Sweep-Line-Verfahren demonstriert
• Präsentation zum Voronoi-Diagramm, Universität Freiburg (PDF-Datei; 287 kB)
• Konstruktion abstrakter Voronoi-Diagramme in O(n log n), Ronny Harbich, 2007

Einzelnachweise

1. ↑ Rolf Klein: Algorithmische Geometrie, Springer 2005, ISBN 978-3-540-20956-0
2. ↑ John Fisher: Visualizing the connection among Convex Hull, Voronoi Diagram and Delaunay Triangulation