Dempster-Shafer-Theorie

Die Evidenztheorie von Dempster und Shafer ist eine mathematische Theorie aus dem Gebiet der Wahrscheinlichkeitstheorie. Sie wird benutzt, um Informationen unterschiedlicher Quellen zu einer Gesamtaussage zusammenzusetzen, wobei die Glaubwürdigkeit dieser Quellen in der Berechnung berücksichtigt wird.

In den 1960er Jahren verfasste Arthur Jeffrey Dempster verschiedene Artikel zu einer Theorie für die Verrechnung von Evidenzen. Die Arbeit Dempsters wurde von Glenn Shafer weiterentwickelt und schließlich 1976 veröffentlicht (Lit.: Shafer, 1976). Die Theorie ist seither bekannt unter der Bezeichnung The Dempster-Shafer Theory of Evidence.

Eine Evidenz kann als eine Erweiterung einer Wahrscheinlichkeit betrachtet werden, wobei statt einem eindimensionalen ein zweidimensionales Maß verwendet wird, welches sich zusammensetzt aus dem Grad des Dafürhaltens bzw. dem Grad des Vertrauens darin, dass die Aussage einer Quelle zutrifft (englisch: degree of belief) und der Plausibilität des Ereignisses bzw. aus einem Wahrscheinlichkeitsbereich mit einer unteren und oberen Grenze.

Die Evidenztheorie findet vor allem dort Einsatz, wo unsichere Aussagen verschiedener Quellen kombiniert werden müssen zu einer Gesamtaussage. Die Evidenztheorie ist in manchen Situationen nicht einsetzbar, da sich der Grad des Vertrauens in eine Quelle nicht beziffern lässt. Dennoch gibt es Anwendungen, wie z. B. in der Mustererkennung, bei denen sich mittels der Evidenztheorie Aussagen verschiedener unzuverlässiger Algorithmen kombinieren lassen, um so eine Aussage zu erhalten, deren Treffsicherheit besser ist als die jeder einzelnen Aussage (Lit.: Garzotto, 1994).

Erläuterndes Beispiel

Nehmen wir an, aufgrund des offiziellen Wetterberichts soll morgen schönes Wetter sein. Nehmen wir weiter an, dass dem Wetterbericht zu 80 % vertraut werden kann, d. h. dass in 80 % aller Fälle der Wetterbericht eine zutreffende Prognose stellt. Wir können nun also zu 80 % annehmen, dass morgen schönes Wetter sein wird. Was aber ist mit den anderen 20 %? Unter Verwendung der herkömmlichen Wahrscheinlichkeitslehre könnte man darauf schließen, dass mit einer Wahrscheinlichkeit von 20 % das Wetter morgen nicht schön sein wird. In diesem Punkt unterscheidet sich die Theorie von Dempster und Shafer von der Wahrscheinlichkeitslehre: In den restlichen 20 % wissen wir nicht, dass das Wetter nicht schön sein wird, sondern wir wissen nichts. Da in 80 % der Fälle die Prognose des Wetterberichts mit Sicherheit zutreffend ist, ist sie es in 20 % nicht mit Sicherheit. Das heißt aber, dass die Aussage des Wetterberichts in 20 % aller Fälle entweder falsch oder richtig sein kann. Die 20 % werden deshalb nicht dem Komplement der Hypothese sondern der Menge aller Hypothesen zugesprochen.

Dieser Unterschied zwischen der Wahrscheinlichkeitslehre und der Theorie von Dempster und Shafer führt zu weiteren Konsequenzen. Der in der Wahrscheinlichkeitslehre für eine Hypothese H gültige Satz

$p(\neg H) = 1 - p(H)$

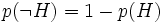
gilt nicht mehr und man kann deshalb anhand der Wahrscheinlichkeit dafür, dass eine Hypothese korrekt ist, nicht mehr bestimmen, welches die Wahrscheinlichkeit dafür ist, dass die Hypothese nicht korrekt ist. Es reicht daher nicht aus, den Glauben für eine Hypothese, in irgendeiner Weise kombiniert mit dem Glauben daran, dass eine Hypothese nicht stimmt, durch einen einzelnen Wert anzugeben. Anstelle eines einzelnen Wertes wird ein Wahrscheinlichkeitsbereich verwendet. Der Bereich ist gegeben durch die untere Grenze bel(H) und die obere Grenze 1 − bel^c(H), d. h. durch die Wahrscheinlichkeit, mit der angenommen werden darf, dass die Hypothese korrekt ist bzw. nicht korrekt ist.

Im obigen Beispiel führt der Wetterbericht zu einer Evidenz für schönes Wetter bel(schoenesWetter) = 0.8. Es gibt aber keinen Grund daran zu glauben, dass morgen nicht schönes Wetter sein wird: bel^c(schoenesWetter) = 0. Anhand des Wetterberichts liegt die Wahrscheinlichkeit für schönes Wetter also im Bereich 0.8 bis 1.0.

Kombination von Evidenzen

Der offizielle Wetterbericht meint wie bisher, morgen soll schönes Wetter sein. Eine andere Quelle, z. B. ein Wetterfrosch, dem nur zu 60 % vertraut werden kann, meint ebenfalls, dass morgen schönes Wetter sein wird. Die folgende Tabelle zeigt, wie die Evidenzen verrechnet werden können:

	Wetterbericht zuverlässig (80 %)	Wetterbericht unzuverlässig (20 %)
Frosch zuverlässig (60 %)	Wetter schön: 80 % * 60 % = 48 %	Wetter schön: 20 % * 60 % = 12 %
Frosch unzuverlässig (40 %)	Wetter schön: 80 % * 40 % = 32 %	Wetter unbestimmt: 20 % * 40 % = 8 %

In drei von vier möglichen Fällen ist die Hypothese schoenesWetter bestätigt, da es sich um zuverlässige Quellen handelt. Es darf also mit 48 % + 12 % + 32 % = 92 % Wahrscheinlichkeit angenommen werden, dass das Wetter morgen schön sein wird. Im vierten Fall (8 %) kann keine Aussage über die Hypothese gemacht werden. Dies bedeutet nun bel(schoenesWetter) = 0.92 und bel^c(schoenesWetter) = 0.

Allgemein können Evidenzen e_i, die alle eine Hypothese H unterstützen, kombiniert werden mit:

bel(H) = 1 − (1 − e₁(H))(1 − e₂(H))...(1 − e_n(H)) und bel^c(H) = 0

und entsprechend Evidenzen, die alle gegen eine Hypothese sprechen mit

bel(H) = 0 und bel^c(H) = 1 − (1 − e₁(H))(1 − e₂(H))...(1 − e_n(H))

Wenn widersprüchliche Evidenzen kombiniert werden sollen, nehmen wir an, der Wetterfrosch behauptet, dass das Wetter nicht schön werde, ergeben sich die folgenden Situationen:

	Wetterbericht zuverlässig (80 %)	Wetterbericht unzuverlässig (20 %)
Frosch zuverlässig (60 %)	unmöglich!: 80 % * 60 % = 48 %	Wetter nicht schön: 20 % * 60 % = 12 %
Frosch unzuverlässig (40 %)	Wetter schön: 80 % * 40 % = 32 %	Wetter unbestimmt: 20 % * 40 % = 8 %

Die Variante, bei der beide Aussagen zutreffen, wird jetzt unmöglich: Wenn beide das Gegenteil behaupten, können nicht beide zuverlässig sein. Nach Dempster und Shafer werden alle möglichen Fälle neu skaliert, so dass die Summe aller Wahrscheinlichkeiten wieder 1 ergibt, d. h. alle Werte für die möglichen Fälle werden durch die Summe aller Werte für die möglichen Fälle dividiert. Daraus ergibt sich:

	Wetterbericht zuverlässig (80 %)	Wetterbericht unzuverlässig (20 %)
Frosch zuverlässig (60 %)	-	Wetter nicht schön: ca. 23 %
Frosch unzuverlässig (40 %)	Wetter schön: ca. 62 %	Wetter unbestimmt: ca. 15 %

Man kann nun also zu etwa 62% annehmen, dass das Wetter schön sein wird und zu etwa 23 %, dass das Wetter nicht schön sein wird. Der Wahrscheinlichkeitsbereich für schönes Wetter ist also begrenzt durch die Werte 0.62 und 0.77 (1 - 0.23). Zwei widersprüchliche Evidenzen e₁(H) (für die Hypothese) und e₂(H) (gegen die Hypothese) können also verrechnet werden zu:

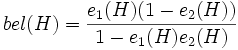$bel(H) = \frac{e_1(H)(1 - e_2(H))}{1 - e_1(H)e_2(H)}$ und

$bel^c(H) = \frac{e_2(H)(1 - e_1(H))}{1 - e_1(H)e_2(H)}$

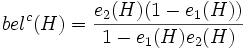
Vorgehen bei mehreren Hypothesen

In den bisherigen Beispielen wurde nur der Fall von einer Hypothese betrachtet. Zudem wurden zwei wichtige Bedingungen für die Theorie von Dempster und Shafer nicht erwähnt: Die Hypothesen müssen sich gegenseitig ausschließen und der Hypothesenraum muss vollständig sein, d. h. die korrekte Hypothese muss in der Menge der vorhandenen Hypothesen vorhanden sein. Im folgenden wird die Vorgehensweise für den allgemeinen Fall mit mehreren, konkurrierenden Hypothesen betrachtet.

Im ersten Beispiel wurden die 20 %, in denen der Wetterbericht unzuverlässig ist, nicht dem Komplement der Hypothese schoenesWetter zugesprochen, sondern sowohl der Hypothese selber als auch deren Komplement, da der Wetterbericht in den 20 % recht haben oder sich irren kann. Bei mehreren Hypothesen wird die Restevidenz, d. h. der Anteil der Evidenzen, der keiner Hypothese zugesprochen werden kann, entsprechend der Gesamtheit der vorhandenen Hypothesen (θ) zugewiesen. Die Zuteilung an die Gesamtheit der Hypothesen ist deshalb sinnvoll, weil angenommen wird, dass der Hypothesenraum vollständig ist.

Sind mehrere Hypothesen vorhanden, dann ist eine Evidenz für eine Hypothese gleichzeitig eine Evidenz gegen die anderen Hypothesen und umgekehrt. Die Evidenz gegen die anderen Hypothesen wird aber, analog zur Restevidenz, nicht unter den anderen Hypothesen aufgeteilt, sondern der Gesamtheit aller anderen Hypothesen zugeschrieben.

Ein Beispiel zu einem Fall mit mehreren Hypothesen: Angenommen ein digitalisiertes Bild, das ein Schriftzeichen darstellt, ist zu klassifizieren. Es liegen drei Hypothesen vor: Das Bild kann ein 'A', ein 'R' oder ein 'B' darstellen, d. h. der Hypothesenraum besteht aus der Menge θ= {'A', 'R', 'B'}. Weiter nehmen wir an, es existiert eine Evidenz von 0.2 für 'R' e₁({'R'}) = 0.2 und eine Evidenz von 0.6 gegen 'A'. Dies führt zu einer Restevidenz e₁(θ) = 0.8 und e₂(θ) = 0.4. Die Evidenz gegen 'A' ist eine Evidenz für 'R' und 'B': e₂({'R','B'}) = 0.6. Die folgende Tabelle fasst die Situation zusammen:

	e1({'R'}) = 0.2	e1(θ) = 0.8
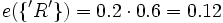
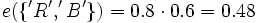
e2({'R','B'}) = 0.6	$e(\lbrace'R'\rbrace) = 0.2 \cdot 0.6 = 0.12$	$e(\lbrace'R', 'B'\rbrace) = 0.8 \cdot 0.6 = 0.48$
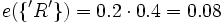
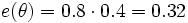
e2(θ) = 0.4	$e(\lbrace'R'\rbrace) = 0.2 \cdot 0.4 = 0.08$	$e(\theta) = 0.8 \cdot 0.4 = 0.32$

Die Evidenzen der Schnittmengen ergeben sich aus dem Produkt der Evidenzen der Mengen, die geschnitten werden. Der Wahrscheinlichkeitsbereich der Hypothesenmenge {H_i} ist gegeben durch:

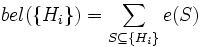$bel(\lbrace H_i \rbrace) = \sum_{S \subseteq \lbrace H_i \rbrace} e(S)$ und

$bel^c(\lbrace H_i \rbrace) = \sum_{S \subseteq \theta \setminus \lbrace H_i \rbrace} e(S)$

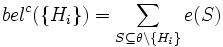
In Worten ausgedrückt: Der Glaube bel({H_i}) daran, dass eine der Hypothesen H_i die richtige ist, ist gegeben durch die Summe der Evidenzen von allen Teilmengen der Hypothesenmenge {H_i} und bel^c({H_i}) durch die Summe aller Evidenzen aller Teilmengen der Komplementärmenge der Hypothesenmenge. Für das Beispiel führt dies zu:

bel({'A'}) = 0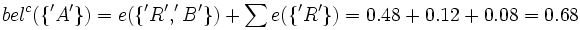

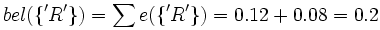
$bel^c(\lbrace'A'\rbrace) = e(\lbrace'R', 'B'\rbrace) + \sum e(\lbrace'R'\rbrace) = 0.48 + 0.12 + 0.08 = 0.68$

$bel(\lbrace'R'\rbrace) = \sum e(\lbrace'R'\rbrace) = 0.12 + 0.08 = 0.2$

bel^c({'R'}) = 0

bel({'B'}) = 0

$bel^c(\lbrace'B'\rbrace) = \sum e(\lbrace'R'\rbrace) = 0.12 + 0.08 = 0.2$

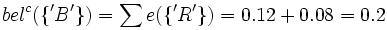
Das Glaubensintervall für 'A' ist also 0 bis 1 - 0.68 also 0 bis 0.32. Jenes für 'R' ist 0.2 bis 1 - 0 also 0.2 bis 1 und das für 'B' ist 0 bis 1 - 0.2 also 0 bis 0.8.

Kommt nun eine weitere Evidenz e₃({'B'}) = 0.3, so ergeben sich die Werte in der folgenden Tabelle:

	e3({'B'}) = 0.3	e3(θ) = 0.7
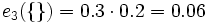
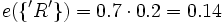
e({'R'}) = 0.2 (aus obiger Tabelle)	$e_3(\lbrace \rbrace) = 0.3 \cdot 0.2 = 0.06$	$e(\lbrace'R'\rbrace) = 0.7 \cdot 0.2 = 0.14$
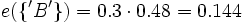
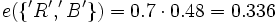
e({'R','B'}) = 0.48 (aus obiger Tabelle)	$e(\lbrace'B'\rbrace) = 0.3 \cdot 0.48 = 0.144$	$e(\lbrace'R', 'B'\rbrace) = 0.7 \cdot 0.48 = 0.336$
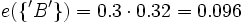
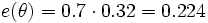
e(θ) = 0.32 (aus obiger Tabelle)	$e(\lbrace'B'\rbrace) = 0.3 \cdot 0.32 = 0.096$	$e(\theta) = 0.7 \cdot 0.32 = 0.224$

Es ergibt sich jetzt eine Evidenz für die leere Menge, was nicht möglich ist, da θ vollständig sein muss. Wie weiter oben beschrieben, müssen die Evidenzen für die möglichen Werte skaliert werden. Daraus ergibt sich schließlich:

bel({'A'}) = 0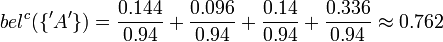

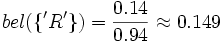
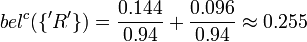
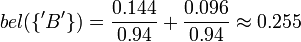
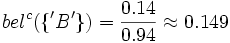
$bel^c(\lbrace'A'\rbrace) = \frac{0.144}{0.94} + \frac{0.096}{0.94} + \frac{0.14}{0.94} + \frac{0.336}{0.94} \approx 0.762$

$bel(\lbrace'R'\rbrace) = \frac{0.14}{0.94} \approx 0.149$

$bel^c(\lbrace'R'\rbrace) = \frac{0.144}{0.94} + \frac{0.096}{0.94} \approx 0.255$

$bel(\lbrace'B'\rbrace) = \frac{0.144}{0.94} + \frac{0.096}{0.94} \approx 0.255$

$bel^c(\lbrace'B'\rbrace) = \frac{0.14}{0.94} \approx 0.149$

Berechnungsverfahren

Wenn eine Menge von n konkurrierende Hypothesen vorhanden ist, müssen möglicherweise 2ⁿ Teilmengen (aus der Potenzmenge von θ) berücksichtigt werden. Werden die Evidenzen in beliebiger Reihenfolge zusammengetragen, dann wird der Aufwand für einen Algorithmus exponentiell. Es kann aber gezeigt werden (Lit.: Barnett 1981), dass ein Algorithmus mit nur linearem Aufwand entsteht, wenn Evidenzen in geschickter Reihenfolge verrechnet werden. Das Verfahren ist ohne Beweis im folgenden beschrieben.

Für jede der konkurrierenden Hypothesen H_i werden alle Evidenzen für die Hypothese verrechnet:

e ⁺ (H_i) = 1 − (1 − e₁(H_i))(1 − e₂(H_i))...(1 − e_n(H_i))

und entsprechend alle Evidenzen e ⁻ (H_i) gegen die Hypothese. Die gesammelten Evidenzen für und gegen die Hypothese können nun kombiniert werden:

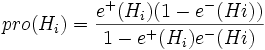$pro(H_i) = \frac{e^+(H_i)(1 - e^-(Hi))}{1 - e^+(H_i)e^-(Hi)}$ und $con(H_i) = \frac{e^-(H_i)(1 - e^+(Hi))}{1 - e^+(H_i)e^-(Hi)}$

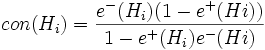
Falls nur eine Hypothese vorhanden ist, dann gilt

bel(H_i) = pro(H_i) und bel^c(H_i) = con(H_i)

Sind mehrere Hypothesen vorhanden, dann muss berücksichtigt werden, dass jede Evidenz für (gegen) eine Hypothese auch eine Evidenz gegen (für) alle anderen Hypothesen darstellt. Diese Evidenzen müssen miteinbezogen werden, so dass sich ergibt:

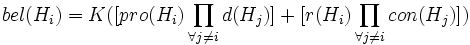$bel(H_i) = K(\lbrack pro(H_i) \prod_{\forall j \neq i} d(H_j) \rbrack + \lbrack r(H_i) \prod_{\forall j \neq i} con(H_j) \rbrack)$ und

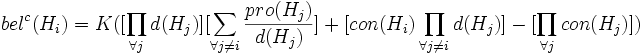$bel^c(H_i) = K(\lbrack \prod_{\forall j} d(H_j)\rbrack \lbrack \sum_{\forall j \neq i} \frac{pro(H_j)}{d(H_j)} \rbrack + \lbrack con(H_i) \prod_{\forall j \neq i} d(H_j) \rbrack - \lbrack \prod_{\forall j} con(H_j) \rbrack)$ wobei r(H_j) = 1 − pro(H_j) − con(H_j) und d(H_j) = 1 − pro(H_j) sowie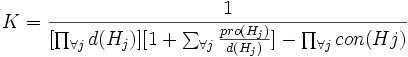 $K = \frac{1}{\lbrack \prod_{\forall j} d(H_j) \rbrack \lbrack 1 + \sum_{\forall j} \frac{pro(H_j)}{d(H_j)} \rbrack - \prod_{\forall j} con(Hj)}$

Dieser Algorithmus kann verwendet werden, wenn nur Evidenzen für oder gegen einzelne Hypothesen vorliegen, d. h. nicht wenn Evidenzen für oder gegen Mengen von Hypothesen vorliegen. Außerdem müssen die Hypothesen sich gegenseitig ausschließen und die Menge der Hypothesen vollständig sein.

Die letzte Bedingung ist in der Realität oft nicht erfüllt, d. h. es ist nicht sichergestellt, dass die korrekte Hypothese Teil der Lösungsmenge ist. Als Lösung für dieses Problem kann zu dem Satz der konkurrierenden Hypothesen eine weitere hinzugefügt werden, die repräsentativ für alle anderen möglichen Hypothesen steht. Diese Erweiterung hat eine Vereinfachung des oben beschriebenen Algorithmus zur Folge, wenn keine Evidenzen für oder gegen diese Hypothese α vorliegen, also pro(α) = con(α) = 0 ist. Dies führt nämlich dazu, dass alle Produkte, in denen pro(α) oder con(α) vorkommen, zu 0 werden und deshalb nicht berechnet werden müssen.

Literatur

• Glenn Shafer: A Mathematical Theory of Evidence. Princeton University Press 1976
• J. A. Barnett: Computational Methods for a Mathematical Theory of Evidence. In: Proc. IJCAI-81, S. 868-875 1981
• Andreas Garzotto: Vollautomatische Erkennung von Schriftzeichen in gedrucktem Schriftgut - Erhöhung der Zuverlässigkeit durch Kombination von unsicherem Wissen aus konkurrierenden Quellen. Dissertation, Universität Zürich 1994