- Denavit-Hartenberg-Transformation
-
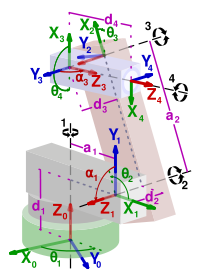
Die Denavit-Hartenberg-Transformation (DH-Transformation) aus dem Jahr 1955 ist ein mathematisches Verfahren, das auf der Basis von homogenen Matrizen und der sogenannten Denavit-Hartenberg-Konvention (DH-Konvention) die Überführung von Ortskoordinatensystemen (OKS) innerhalb von kinematischen Ketten beschreibt. Sie erleichtert so vor allem die Berechnung der direkten Kinematik (Vorwärtskinematik) und gilt hierbei mittlerweile als das Standardverfahren, insbesondere im Bereich Robotik.
Inhaltsverzeichnis
DH-Konvention
Folgende Voraussetzungen sind notwendig:
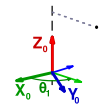
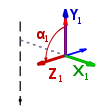
- die zn-Achse liegt entlang der Bewegungsachse des n-ten Gelenks
- die xn-Achse ist das Kreuzprodukt von zn und zn − 1.
- das Koordinatensystem wird mit der yn-Achse ergänzt so dass es ein rechtshändiges System ergibt.
Für das erste Gelenk wird die x Achse von dem zweiten Gelenk übernommen.
DH-Transformation
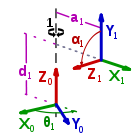
Die eigentliche DH-Transformation vom Objektkoordinatensystem (OKS) Tn − 1 in das OKS Tn besteht in der Hintereinanderausführung folgender Einzeltransformationen:
- einer Rotation θn (Gelenkwinkel) um die zn − 1-Achse, damit die xn − 1-Achse parallel zu der xn-Achse liegt
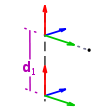
- einer Translation dn (Gelenkabstand) entlang der zn − 1- Achse bis zu dem Punkt, wo sich zn − 1 und xn schneiden
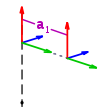
- einer Translation an (Armelementlänge) entlang der xn-Achse, um die Ursprünge der Koordinatensysteme in Deckung zu bringen
- einer Rotation αn (Verwindung) um die xn-Achse, um die zn − 1-Achse in die zn-Achse zu überführen
In Matrixschreibweise lautet die Gesamttransformation dann (von links nach rechts zu interpretieren):
Die Invertierte dieser Matrix
beschreibt die Transformation eines Punktes vom OKS Tn ins OKS Tn − 1. Entsprechend kann die ursprüngliche Matrix n − 1Tn auch als Transformation eines Punktes vom OKS Tn − 1 ins OKS Tn interpretiert werden, wenn der Ortsvektor des Punktes von rechts an die Matrix multipliziert wird.
Die Parameter θn,dn,an und αn werden dabei auch Denavit-Hartenberg-Parameter genannt.
Bei offenen kinematischen Ketten sind θn und dn variable Größen während der Bewegung des Roboters, abhängig von dessen spezieller Geometrie und Maßen. Bei einem rotatorischem Gelenk ist θn variant und dn konstant, bei einem Schubgelenk umgekehrt. αn und an dagegen sind sowohl bei Rotations-, als auch bei Schubgelenken invariante Größen und müssen für die spätere Berechnung der direkten Kinematik nur einmal für jedes einzelne Armelement bestimmt werden.
Weblinks
- Eine Visualisierung zur Ermittlung der Denavit-Hartenberg-Parameter in englischer Sprache verfügbar unter: YouTube, 1280x720 MPEG-4, 640x360 MPEG-4
- Denavit-Hartenberg Parameters (englisch)
Literatur
- Hans-Jürgen Siegert, Siegfried Bocionek: Robotik, Programmierung intelligenter Roboter. Springer Verlag 1996, ISBN 3-540-60665-3.
- Wolfgang Weber: Industrieroboter, Methoden der Steuerung und Regelung. Carl Hanser Verlag, München Wien, 2009, ISBN 978-3-446-41031-2.
- Jorge Angeles: Fundamentals of Robotic Mechanical Systems. Springer Verlag, New York, 1997, ISBN 0-387-94540-7.
- Friedrich Pfeiffer, Eduard Reithmeier: Roboterdynamik. Teubner Verlag, Stuttgart, 1987, ISBN 3-519-02077-7.
- Miomir Vukobratvic: Introduction to Robotics. Springer Verlag, Berlin, 1989, ISBN 0-387-17452-4.
- John J. Craig: Introduction to Robotics, Mechanics and Control. Pearson Prentice Hall, NJ 07458, 2005, ISBN 0-201-54361-3.
Wikimedia Foundation.