Technische Mechanik

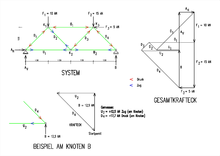
Cremonaplan als ein klassisches Beispiel für die Lösung eines Problemes innerhalb der Technischen Mechanik

Die Technische Mechanik ist ein Teilgebiet der Ingenieurwissenschaften. Ihre naturwissenschaftliche Grundlage ist die klassische Mechanik, die ihrerseits ein Teilgebiet der Physik ist. Das Aufgabengebiet der Technischen Mechanik ist die Bereitstellung der theoretischen Berechnungsverfahren beispielsweise für die Materialwissenschaft, den Maschinenbau und die Baustatik. Die eigentliche Bemessung, Auswahl der Werkstoffe und dergleichen mehr wird dann von diesen anwendungsnahen Disziplinen übernommen, in denen die Technische Mechanik Hilfswissenschaft ist.

Gegenstände der Technischen Mechanik sind:

• die Gesetze der Klassischen Mechanik
• mathematische Modelle der mechanischen Zusammenhänge physischer Körper,
• spezifische und rationelle Methoden der rechnerischen Analyse mechanischer Systeme.

Teilgebiete der Technischen Mechanik

Die Einteilung der Technischen Mechanik ist nicht überall einheitlich. Im Allgemeinen können als Teilgebiete der Technischen Mechanik gelten:

• Kinematik: Die Bewegung der Körper, ohne Berücksichtigung von Kräften
• Dynamik: Die Mechanik von Körpern unter Krafteinwirkung
  • Statik: Die Mechanik der ruhenden Körper
    • Theorie der Stabwerke sowie der Flächen- und Raumtragwerke
  • Kinetik: Die Bewegung der Körper unter dem Einfluss von Kräften
    • Reibungslehre als ein Spezialfall der Kinetik
    • Schwingungslehre: Der Spezialbereich der Kinetik der Schwingungsanalyse von Körpern
    • Mechanik des Stoßes: Ein Spezialbereich der Kinetik der kurzzeitigen Krafteinwirkungen in Körpern
• Kontinuumsmechanik
  • Elastizitätstheorie: Die Verallgemeinerung des Hookeschen Gesetzes
  • Plastizitätstheorie: Untersuchungen zu den Gesetzmäßigkeiten im nicht-hookeschen Bereich
• Festigkeitslehre (Elasto- und teilweise Plastomechanik): Die Untersuchung der Widerstandsfähigkeit von belasteten Körpern nach der Theorie I. Ordnung
  • Fließgelenktheorie: Die Erweiterung der Festigkeitslehre in den plastischen Bereich
  • Kerbspannungslehre: Ein Spezialbereich der Festigkeitslehre und Grenzbereich der Technischen Mechanik zur Werkstoffkunde

spezielle Gebiete:

• Stabilitätstheorie: Die Untersuchung von dynamischer Bewegungsstabilität oder der Stabilität von belasteten Körpern gegen Bruch nach der Theorie II. Ordnung (wie etwa Knickungsvorgänge)
• Maschinendynamik
• Bodenmechanik (beschreibt Verformungen und Spannungen in Kontinua (z. B. Halbräumen) mit Stoffgesetzen, die den realen Stoffgesetzen von Böden nahekommen)
• Biomechanik: Die mechanische Untersuchung lebender Strukturen
• Viskoelastizitätstheorie: Ein Sondergebiet der Kontinuumsmechanik, das sich mit der Untersuchung viskoelastischer Medien befasst
• Kontaktmechanik: Untersuchungen zur statischen und dynamischen (wälzenden oder abrollenden) Berührung von Körpern, insbesondere Erstellung von Modellen zur Flächenpressung in der Berührzone.

Im Wesentlichen kann man den Bereich der Technischen Mechanik auf die Ermittlung der Spannungen und Verformungen elastischer Körper sowie der Bewegungen von Festkörpern eingrenzen. Die Ruhe eines Körpers als wichtiger Grenzfall der Bewegung wird in der Technischen Mechanik mit Hilfe der Statik bestimmt. Neben der klassischen Technischen Mechanik, die eine geschlossene mathematische Beschreibung in Differentialgleichungen anstrebt, gewinnt die Erarbeitung numerischer Methoden zunehmende Bedeutung. Thermodynamik und Strömungslehre (Hydraulik, Fluidmechanik) gelten gewöhnlich nicht als Bestandteile der Technischen Mechanik, sondern als eigenständige Teilgebiete der Ingenieurwissenschaften.

Weitere spezielle Teilgebiete der Technischen Mechanik sind die Lageberechnungen und -regelung der Satelliten und die Ballistik.

Geschichte der Technischen Mechanik

Den meisten Menschen ist es aus der eigenen Intuition heraus gegeben, elementare Probleme der Statik und der Dynamik zu lösen, ohne sich des eigentlichen Hintergrundes bewusst zu sein. Als ein ganz typisches Beispiel für diese Annahme gilt in der Statik der Träger, über dessen Belastbarkeit man schon aus der bloßen Anschauung heraus recht genaue Angaben machen kann.

Formal wurde die Technische Mechanik bereits von Archimedes betrieben, jedoch sind analytisch verwertbare Erkenntnisse erst aus der Zeit der ersten Hälfte des 17. Jahrhunderts überliefert. Die damaligen Mathematiker wurden von den anschaulichen Gesetzen der Mechanik zu ihren neuen Erkenntnissen inspiriert, gleichzeitig entdeckten sie eine Reihe neuer Erkenntnisse und mathematischer Gesetzmäßigkeiten der Technischen Mechanik. In den folgenden Jahrhunderten wurden ihre Theorien in die Technik eingeführt und praktisch umsetzbar gemacht, während weitere theoretische Erkenntnisse folgten. Zeitgleich berechneten die Praktiker den ballistischen Flug einer Kanonenkugel und suchten andererseits die Wirkung dieser Kanonenkugel auf die Mauern einer Festung durch eine geschickte Wahl der äußeren Abmessungen der Festung zu minimieren.

Illustration eines durch eine äußere Last belasteten Balkens in Galileis Discorsi

Der Grieche Archimedes war der erste Mathematiker, der sich eingehend mit mechanischen Problemen befasste. Er entdeckte die Gesetze der Hydrostatik, so wie sie heute noch Gültigkeit besitzen. Simon Stevin entwarf das Kräfteparallelogramm durch das nach ihm benannte Stevinsches Gedankenexperiment. Johannes Kepler beschrieb die Bewegungen der Planeten und Monde mit mathematischen Hilfsmitteln. Die dabei entdeckten Keplerschen Gesetze werden auch heute noch zur Bahnberechnung künstlicher Satelliten und Raumsonden verwendet.

Galileo Galilei kommt in der beginnenden Neuzeit das Verdienst zu, die gerade entstehende Wissenschaft der Technischen Mechanik auf eine formale mathematische Grundlage gestellt zu haben. Der zweite Tag seiner Discorsi befasst sich im Wesentlichen mit der Diskussion von Festigkeitsproblemen. Im gleichen Sinne wirkte Isaac Newton, der mit der Erfindung der Infinitesimalrechnung basierend auf mechanischen Beobachtungen Wissenschaftsgeschichte schrieb. Christiaan Huygens lieferte schon praktische Ergebnisse seiner Forschungen in Form der Pendeluhr und genaueren Erkenntnissen der Astronomie. Die Mitglieder der Familie Bernoulli bereiteten im 18. Jahrhundert neben weiteren theoretischen Erkenntnissen den Boden für eine noch heute gültige Technische Mechanik, welche die Grundlage für viele Disziplinen der Technik bildet. Leonhard Euler benannte die Theorien zur Knickung, zur Balkenbiegung und zum Verständnis der modernen Turbinen. Im gleichen Zeitraum begründete Charles Augustin de Coulomb die Grundlagen der Reibungslehre, die ein verbessertes Verständnis für das Funktionieren der gleichzeitig erfundenen Maschinen lieferte. Eine ebenfalls mehr auf die Belange der Praxis abgestimmte Technische Mechanik entwickelten im 19. Jahrhundert Karl Culmann, August Ritter, Giuseppe Cremona und Carlo Alberto Castigliano. Ihre Lösungen mechanischer Probleme basierten mangels leistungsfähiger Rechenmaschinen im Wesentlichen auf exakten geometrischen Zeichnungen. Ein weiterer, bedeutender Name aus der Zeit Ende des 19. und Anfang des 20. Jahrhunderts im Bereich der Technischen Mechanik ist Christian Otto Mohr, von dem die Untersuchen zum Mohrschen Kreis stammen und der zur selben Zeit an der Technischen Universität Dresden lehrte wie Ludwig Burmester, der Erfinder der gleichnamigen Schablonen.^[1]

Im 20. Jahrhundert entstanden für die Bedürfnisse der Luft- und Raumfahrt die Aerodynamik durch Ludwig Prandtl und Theodore von Kármán. Gleichzeitig entwickelten John Argyris und andere Mathematiker die Finite-Elemente-Methode. Der in den dreißiger Jahren sich zur Blüte entwickelnde Hochbau verwendete iterative Verfahren für die statische Berechnung, wie sie von Gaspar Kani oder Hardy Cross veröffentlicht wurden. Alle diese Verfahren nutzen die Numerik als wesentlichen Ansatz.

Viele der genannten Personen haben auch auf anderen Gebieten große Verdienste erworben (z. B. in der Hydromechanik, Optik, Elektrotechnik, Relativitätstheorie und Quantenmechanik). Andererseits war die Technische Mechanik Namensgeberin für eine ganze Klasse mathematischer Objekte: Die Tensoren wurden nach dem Spannungstensor benannt, der im Zusammenhang mit der Elastizitätstheorie eingeführt wurde.

Literatur

• István Szabó: Einführung in die Technische Mechanik, 8. neu bearbeitete Auflage 1975, Nachdruck 2003 ISBN 3-540-44248-0
• R. C. Hibbeler: Technische Mechanik 1 – Statik. 10., überarbeitete Aufl. Pearson Studium, München 2005, 8., neu bearbeitet Auflage 1975, Nachdruck. 2003 ISBN 3-8273-7101-5
• R. C. Hibbeler: Technische Mechanik 2 – Festigkeitslehre. 5., überarbeitete und erweiterte Aufl. Pearson Studium, München 2005, ISBN 3-8273-7134-1
• R. C. Hibbeler: Technische Mechanik 3 – Dynamik. 10., überarbeitete und erweiterte Aufl. Pearson Studium, München 2006, ISBN 3-8273-7135-X
• Gross/Hauger/Schröder/Wall: Technische Mechanik 1 – Statik. 10., bearbeitete Aufl. Springer, Berlin 2008, ISBN 978-3-540-68394-0
• Gross/Hauger//Schröder/Wall: Technische Mechanik 2 – Elastostatik. 10., bearbeitete Aufl. Springer, Berlin 2009, ISBN 978-3-642-00564-0
• Gross/Hauger/Schröder/Wall: Technische Mechanik 3 – Kinetik. 10., bearbeitete Aufl. Springer, Berlin 2008, ISBN 978-3-540-68422-0
• Gross/Hauger/Wriggers: Technische Mechanik 4 – Hydromechanik, Elemente der Höheren Mechanik, Numerische Methoden. 7. Aufl. Springer, Berlin 2009, ISBN 978-3-540-89390-5
• István Szabó: Geschichte der mechanischen Prinzipien und ihrer wichtigsten Anwendungen, Birkhäuser Verlag, ISBN 3-7643-1735-3
• Mahnken: Lehrbuch der Technischen Mechanik – Dynamik. 1. Aufl. Springer, Berlin 2010, ISBN 978-3-540-36040-7
• Wriggers/Nackenhorst/Beuermann/Spiess/Löhnert: Technische Mechanik kompakt, 2. Auflage, Teubner-Verlag, Stuttgart, 2006, ISBN 978-3-8351-0087-9
• Helga Dankert / Jürgen Dankert: Technische Mechanik Statik, Festigkeitslehre, Kinematik/Kinetik, 4. korr. u. erg. Auflage, Teubner-Verlag, 2006, ISBN 3-8351-0006-8

Einzelnachweise

1. ↑ 100 Jahre Zeunerbau, incl. Bild von Otto Mohr und Darstellung zum Mohrschen Kreis

Weblinks

•  Wikibooks: Die Mechanik starrer Körper – Lern- und Lehrmaterialien
•  Wikibooks: Die Mechanik realer Körper – Lern- und Lehrmaterialien
•  Wikibooks: Dynamik – Lern- und Lehrmaterialien
• engl. Wikibook zum Thema Festkörpermechanik