- Dirichlets Approximationssatz
-
Der dirichletsche Approximationssatz ist ein mathematischer Satz über die Qualität der Approximation (Annäherung) reeller Zahlen durch rationale Zahlen. Er besagt, dass es zu jeder reellen Zahl α und jeder positiven ganzen Zahl N eine ganze Zahl q mit
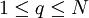 gibt, sodass der Abstand von qα zur nächsten ganzen Zahl höchsten gleich 1 / (N + 1) ist. In mathematischer Schreibweise: Zu
gibt, sodass der Abstand von qα zur nächsten ganzen Zahl höchsten gleich 1 / (N + 1) ist. In mathematischer Schreibweise: Zu 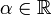 existieren ein
existieren ein 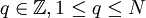 und ein
und ein 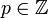 , sodass
, sodass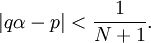
Bewiesen wird dieser nach Peter Gustav Lejeune Dirichlet benannte Satz mithilfe des Schubfachprinzips.
Als Schlussfolgerung daraus ersieht man, dass es zu jedem reellen α unendlich viele Paare (p,q) positiver ganzer Zahlen gibt, die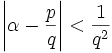
erfüllen. Dass diese Abschätzung nicht beliebig verbessert werden kann, besagt der (ungleich komplizierter zu beweisende) Satz von Thue-Siegel-Roth.
Beispiel: Sei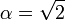 , und N = 10. Dann ist nach dem dirichletschen Approximationssatz eine der Zahlen
, und N = 10. Dann ist nach dem dirichletschen Approximationssatz eine der Zahlen 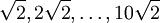 um höchstens 1 / 11 von einer ganzen Zahl entfernt. Tatsächlich ist
um höchstens 1 / 11 von einer ganzen Zahl entfernt. Tatsächlich ist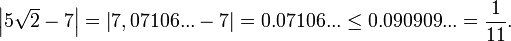
Wikimedia Foundation.
