- Dirichletscher Schubfachschluss
-
In der Mathematik ist das Schubfachprinzip (engl. pigeonhole principle, daher auch Taubenschlagprinzip) eine einfache und effiziente Methode, um gewisse Aussagen über eine endliche Menge zu machen. Das Prinzip wird oft in der diskreten Mathematik benutzt. Es beschreibt eigentlich eine Selbstverständlichkeit.
Inhaltsverzeichnis
Das Prinzip
Das Prinzip kann folgendermaßen formuliert werden:
- Falls man n Objekte auf m Mengen (n,m > 0) verteilt, und n größer als m ist, dann gibt es mindestens eine Menge, in der mehr als ein Objekt landet.
Der Name kommt von einer bildhaften Vorstellung dieses Vorgangs: Falls man eine bestimmte Anzahl von Schubfächern hat, und man mehr Objekte in die Fächer legt als Fächer vorhanden sind, dann landen in irgendeinem Schubfach mindestens zwei dieser Objekte.
Es geht wahrscheinlich auf Dirichlet zurück, der es 1834 angewandt hat. Im Russischen wird es daher auch „Dirichlet-Prinzip“ genannt.
Beweis
Der Beweis dieses Prinzips ist beinahe trivial und kann zum Beispiel mittels Widerspruch geführt werden: Falls das Prinzip nicht stimmt, dann landet in jedem Schubfach höchstens ein Objekt. Damit gibt es höchstens so viele Objekte wie Schubfächer. Das steht aber im Widerspruch zur Voraussetzung, dass es mehr Objekte als Schubfächer gibt.
Beispiel
Trotz seiner Einfachheit kann man mit dem Schubfachprinzip interessante Aussagen treffen, zum Beispiel die, dass es in München mindestens zwei Personen gibt, die exakt dieselbe Anzahl von Haaren auf dem Kopf haben. Beweis: Man teilt alle Bewohner Münchens nach der Anzahl ihrer Haare in „Schubfächer“ ein. Typischerweise hat der Mensch etwa 100.000 bis 200.000, jedoch sicher nicht mehr als 1 Million Haare, damit gibt es maximal eine Million Schubfächer. Da es aber etwa 1,3 Millionen Einwohner in München gibt, hat man mehr Einwohner als Schubfächer, damit landen in mindestens einem Schubfach zwei Personen. Diese haben nach Definition der Schubfächer dieselbe Anzahl Haare auf dem Kopf.
Verschärfung des Prinzips
Eine "schärfere" Fassung des Taubenschlagprinzips lautet wie folgt:
- Verteilt man n Objekte auf k Mengen (n,k > 0) und ist dabei n > k, so gibt es mindestens eine Menge, in der sich mehr als
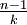Objekte befinden.
Beispiel der Verschärfung
Damit kann man jetzt beweisen, dass wenn es in Deutschland mindestens 82 000 001 Einwohner gibt und ein Mensch wiederum nicht mehr als 1 000 000 Haare besitzen soll, es mindestens zweiundachzig Deutsche gleicher Haaranzahl gibt: Wir verteilen 82 000 001 Objekte (Deutsche) auf 1 000 000 Mengen (die die Haaranzahl ihrer Elemente [Objekte] wiedergeben), also gibt es mindestens eine Menge mit mehr als
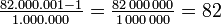Objekten.Verwandte Themen
Mit kombinatorischen Verallgemeinerungen des Prinzips befasst sich die Ramseytheorie.
Literatur und Weblinks
- Martin Aigner und Günter M. Ziegler: Das Buch der Beweise, Berlin (Springer) 2002
- Pigeon Principle bei cut-the-knot (engl.; mit math. Beispielen)
Wikimedia Foundation.
