- Agrawal-Kayal-Saxena-Primzahltest
-
Der AKS-Primzahltest (auch bekannt unter dem Namen Agrawal-Kayal-Saxena-Primzahltest) ist ein deterministischer Algorithmus, der für eine Zahl in polynomieller Laufzeit feststellt, ob sie prim ist oder nicht. Er wurde von den drei indischen Wissenschaftlern Manindra Agrawal, Neeraj Kayal und Nitin Saxena entdeckt und 2002 in einer Abhandlung mit dem Titel PRIMES is in P (deutsch sinngemäß: Das Primzahl-Problem gehört zur Komplexitätsklasse P) veröffentlicht.
Der später von anderen verbesserte Algorithmus unterscheidet sich wesentlich von allen vorher bekannten polynomiellen Primalitäts-Beweisalgorithmen: Er baut für den Nachweis der – bezogen auf die Länge der Eingangswerte – polynomiellen Laufzeit auf keinen unbewiesenen Hypothesen (wie beispielsweise der verallgemeinerten Riemannschen Vermutung) auf. Die asymptotische Laufzeit des ursprünglichen Algorithmus ist
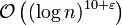 (Landau-Symbol
(Landau-Symbol 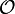 ), wobei n die zu testende Zahl ist.
), wobei n die zu testende Zahl ist.Inhaltsverzeichnis
Entstehungsgeschichte
1999 arbeitete Manindra Agrawal mit seinem Doktorvater Somenath Biswas an einer probabilistischen Methode, um die Gleichheit von Polynomen zu zeigen. Die beiden erarbeiteten daraus eine Methode für einen probabilistischen Primzahltest. Die Idee, die dahinter steckt und die sich später als sinnvoll herausstellte, ist folgendes Lemma:
Sei
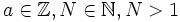 und ggT(a,N)=1. Dann ist
und ggT(a,N)=1. Dann ist 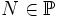 genau dann, wenn
genau dann, wenn 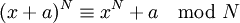
Für den so entstandenen Primzahltest galt, dass er nicht mit den aktuellen mithalten konnte. Im schlimmsten Falle musste man alle Koeffizienten berechnen, was ziemlich aufwendig sein konnte. Deshalb wurde die Idee zunächst nicht weiter verfolgt.
2001 nahmen die Studenten Rajat Bhattarcharjee und Prashant Pandey in ihrer Bachelorarbeit Primality Testing die Idee wieder auf. Sie erweiterten die Idee, die Polynome nicht nur modulo N sondern auch modulo xr − 1 für ein r in der Größenordnung von logN zu berechnen. Dies hat den Vorteil, dass man
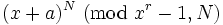 in polynomieller Zeit berechnen kann. Nun gilt für eine Primzahl N, dass sie diese Kongruenz erfüllt, aber es erfüllen sie nun auch Zahlen, die keine Primzahlen sind.
in polynomieller Zeit berechnen kann. Nun gilt für eine Primzahl N, dass sie diese Kongruenz erfüllt, aber es erfüllen sie nun auch Zahlen, die keine Primzahlen sind.Die beiden untersuchten diese Kongruenz für bestimmte a und r, um Bedingungen an a und r zu stellen, damit diese Kongruenz nur noch für Primzahlen gilt. Sie stellten nach einer Versuchsreihe die folgende Vermutung auf:
Ist
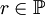 kein Teiler von N und
kein Teiler von N und 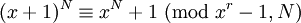 , dann ist N entweder Prim oder
, dann ist N entweder Prim oder 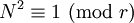 .
.2002 arbeiteten die beiden Studenten Neeraj Kayal und Nitin Saxena an ihrer Bachelorarbeit. Sie führten die Überlegungen ihrer Vorreiter weiter. Unter der Annahme, dass die Riemannsche Vermutung korrekt ist, konnten sie den obigen Satz beweisen. In einer leichten Vorahnung nannten sie dann ihre Bachelorarbeit: Towards a deterministic polynomial-time Primality Test.
Danach schafften sie es mit Manindra Agrawal, den Algorithmus in seine endgültige Form zu bringen. Die dann veröffentlichte Schrift erfreute sich ziemlich schnell einer großen Beliebtheit. So wurde die Korrektheit innerhalb einer Woche bestätigt und die Webseite hatte über zwei Millionen Besuchern in der ersten Woche.
Die Beliebtheit dieser Schrift kann man damit erklären, dass dieses Problem eines der großen der aktuellen Mathematik ist, aber so einfach nachzuvollziehen ist.
Der Algorithmus
Im folgenden sind
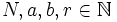 . Die Eingabe ist die Zahl N>1.
. Die Eingabe ist die Zahl N>1.1. if N = ab for b>1 return ZUSAMMENGESETZT
2. finde das kleinste r mit or(N) > 4(logN)2
3. if 1<ggT(a,N)<N für ein
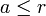 return ZUSAMMENGESETZT
4. if
return ZUSAMMENGESETZT
4. if 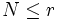 return PRIM
5. for a=1 to
return PRIM
5. for a=1 to 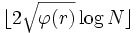 do
if
do
if 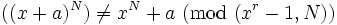 return ZUSAMMENGESETZT
6. return PRIM
return ZUSAMMENGESETZT
6. return PRIM
Man sollte noch bemerken, dass or(N) die Ordnung von N modulo r und
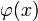 die Eulersche Phi-Funktion bezeichnet. Die Ordnung von N modulo r bezeichnet die kleinste Zahl k, für die
die Eulersche Phi-Funktion bezeichnet. Die Ordnung von N modulo r bezeichnet die kleinste Zahl k, für die 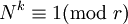 gilt.
gilt.Nach Agrawal, Kayal und Saxena
In den folgenden Monaten nach der Entdeckung erschienen neue Varianten (Lenstra 2002, Pomerance 2002, Berrizbeitia 2003, Cheng 2003, Bernstein 2003a/b, Lenstra und Pomerance 2003), die die AKS-Geschwindigkeit um Größenordnungen verbesserten. Wegen der großen Anzahl an Varianten sprechen Crandall und Papadopoulos in ihrem Aufsatz On the implementation of AKS-class primality tests (Über die Implementation von Primzahltests der AKS-Klasse) von März 2003 von der Klasse der AKS-Algorithmen, statt vom AKS-Algorithmus.
Der Algorithmus von Lenstra und Pomerance terminiert in
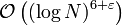 .
.Agrawal, Kayal und Saxena haben mit der obigen Vermutung einen ähnlichen Algorithmus aufgestellt:
Man suche zuerst ein
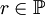 mit
mit 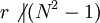 (so ein r liegt im Intervall 2,4logN). Mit diesem Algorithmus erhält man eine Laufzeit von
(so ein r liegt im Intervall 2,4logN). Mit diesem Algorithmus erhält man eine Laufzeit von 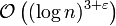
Weblinks
- MathWorld: AKS Primality Test
- PRIMES is in P: Scientific paper describing AKS primality test (PDF)
- R. Crandall, Apple ACG, and J. Papadopoulos (March 18, 2003): On the implementation of AKS-class primality tests (PDF)
- Artikel von Folkmar Bornemann über den AKS-Primzahltest mit Fotos der drei indischen Forscher (PDF)
Wikimedia Foundation.
