Primzahlentest

Als Primzahltest bezeichnet man ein mathematisches Verfahren, mit dem ermittelt wird, ob eine gegebene Zahl eine Primzahl ist oder nicht.

Praktische Anwendung

In der Praxis werden Primzahltests insbesondere bei asymmetrischen Verschlüsselungsverfahren in der Kryptographie eingesetzt. Algorithmen wie RSA benötigen Primzahlen in einer Größenordnung von etwa 1000 Stellen in dualer Darstellung. Es ist also unmöglich, diese alle zu berechnen und in einer Liste zu speichern um bei Bedarf einfach darauf zuzugreifen. Auch die Vorausberechnung einer Teilmenge ist aus sicherheitstechnischen Gründen fragwürdig, da die Liste Angreifern in die Hände fallen könnte. Statt der Verwendung einer bekannten Primzahl rät der Algorithmus (mit ein paar Tricks) eine „beliebige“ Zahl und stellt mit Hilfe eines Primzahltests möglichst schnell fest, ob diese tatsächlich prim ist.

Da „echte“ Primzahltests bei Zahlen dieser Größe zu lange dauern, wird meist ein Monte-Carlo-Algorithmus verwendet, mit dem in Wirklichkeit gar nicht sicher festgestellt werden kann, ob die gegebene Zahl eine Primzahl ist. Es kann dabei aber die Wahrscheinlichkeit, eine zusammengesetzte Zahl fälschlicherweise für eine Primzahl zu halten, beliebig tief (nur eben nicht auf 0) gedrückt werden. Zwar würde die Verwendung einer Nicht-Primzahl als kryptographischer Schlüssel eine unsichere Verschlüsselung bedeuten, doch wenn die Wahrscheinlichkeit dafür milliardenmal geringer ist als die, dass Absender und Empfänger der Nachricht gleichzeitig vom Blitz getroffen werden, wird dieses Risiko in Kauf genommen, um das ansonsten sehr sichere Verschlüsselungsverfahren verwenden zu können.

Bekannte Primzahltest-Verfahren

Es gibt zahlreiche Ansätze für Primzahltests:

Probedivision

Hauptartikel: Probedivision

Der einfachste Primzahltest ist die Probedivision. Dabei probiert man nacheinander, ob die Zahl n durch eine der Zahlen zwischen 2 und 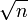$\sqrt{n}$ teilbar ist. Ist sie das nicht, dann ist n eine Primzahl. Die Probedivision ist jedoch viel zu aufwändig, sodass sie in der Praxis als Primzahltest nicht zum Einsatz kommt.

Sieb des Eratosthenes

Hauptartikel: Sieb des Eratosthenes

Das Sieb des Eratosthenes ist eigentlich ein Algorithmus um eine Liste von Primzahlen zu erzeugen. Da diese Liste bis zu einer frei wählbaren Grenze alle Primzahlen enthält, kann sie für einen Primzahltest verwendet werden. Man überprüft dazu lediglich, ob die übergegebene Zahl in der Liste ist.

Fermatscher Primzahltest

• den Fermatschen Primzahltest, der allerdings nur dann Primzahlen von Pseudoprimzahlen mit 100%iger Sicherheit unterscheiden kann, wenn er zu jeder zu prüfenden Zahl alle möglichen Primbasen durchprüft, die kleiner als die zu prüfende Zahlen sind. Damit ist dieses Verfahren das langsamste Verfahren.
  

Der zum Fermatschen Primzahltest gehörige Quell-Code

• Der Lucas-Test ist eine Verbesserung des Fermatschen Primzahltests.

• Der ARCL-Test ist eine Verbesserung des Fermatschen Primzahltests. Der Name besteht aus den Initialen der Mathematiker Leonard Adleman, R.S.Rumely, H.Cohen und H.W.Lenstra Jr.

• Der Lucas-Lehmer-Test zum Prüfen von Mersenne-Primzahlen.

Solovay-Strassen

• Der Solovay-Strassen-Test ist ein Monte-Carlo-Algorithmus, bei dem aber im Allgemeinen die Anzahl der falschen Zeugen größer ist als beim Miller-Rabin-Test.

Miller-Rabin

• Der Miller-Rabin-Test ist ein Monte-Carlo-Algorithmus, der durch die Randomisierung eine akzeptable Laufzeit erreicht, sowie schon nach wenigen Durchführungen mit hoher Wahrscheinlichkeit das korrekte Ergebnis gefunden hat.
  
  

Zufalls-Primzahlentest	beruht auf	Art der auftretenden Pseudoprimzahlen
Fermatscher Primzahltest	kleiner Fermatscher Satz	Fermatsche Pseudoprimzahlen
Solovay-Strassen-Test	Satz nach Euler und Jacobi-Symbol	Eulersche Pseudoprimzahlen
Miller-Rabin-Test	Satz nach Miller	starke Pseudoprimzahlen

AKS-Methode

• Die AKS-Methode ist ein Primzahltest in Polynomialzeit, der im Jahr 2002 von Manindra Agrawal, Neeraj Kayal und Nitin Saxena gefunden und nach ihnen benannt wurde.

Primzahltests in der Komplexitätstheorie

Die den Primzahltest zugrundeliegende Problemstellung, festzustellen, ob eine Zahl prim ist, wird in der Informatik als PRIMES bezeichnet. Bis ins Jahr 2002 erhoffte man sich in der Komplexitätstheorie von ihr neue Erkenntnisse in Bezug auf das P-NP-Problem. Falls P≠NP gilt, muss nach dem Satz von Ladner ein Problem in NP\P existieren, welches nicht NP-vollständig ist^[1]. PRIMES galt als ein potenzieller Kandidat für ein solches Problem.

Dies lag daran, dass PRIMES sowohl in der Komplexitätsklasse NP als auch in der Komplexitätsklasse co-NP liegt, und demnach nicht NP-vollständig sein konnte. Man kannte jedoch keinen nicht-probabilistischen Lösungsalgorithmus mit polynomieller Laufzeit. Daher war es fraglich, ob PRIMES auch in der Komplexitätsklasse P liegt.

2002 wurde jedoch von Agrawal, Kayal und Saxena mit dem AKS-Primzahltest ein solcher polynomieller Primzahltest gefunden. Damit war die lange Zeit offene Frage, ob PRIMES in P liegt, beantwortet. Dies brachte jedoch keine weitere Erkenntnis zum P-NP-Problem.

Quellen

1. ↑ R. E. Ladner: On the structure of polynomial time reducibility, J.ACM, 22, pp. 151–171, 1975. Corollary 1.1. ACM Eintrag.

Weblinks

• Ein Überblick über verschiedene Primzahltestverfahren von D. Bernstein (engl.)