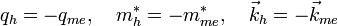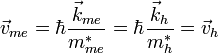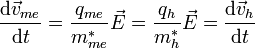Elektronenfehlstelle

Als Defektelektron, Elektronenfehlstelle oder Loch wird der (gedachte) positive bewegliche Ladungsträger in Halbleitern bezeichnet und stellt die äquivalente Beschreibung des Fehlens eines (realen) Valenzelektrons dar^[1]. Der reale Ladungstransport findet weiterhin durch Elektronen statt, es handelt sich lediglich um eine alternative Beschreibung zur Vereinfachung der mathematischen Behandlung der Vorgänge im Halbleiter.

Beschreibung

Das Defektelektron entsteht zum Beispiel durch Ionisation von Fremdatomen (Fremdleitung), in hochreinen Halbleitern (Silicium, Germanium, Galliumarsenid etc. gezielt mit gewissen drei- bzw. fünfwertigen Elementen (meist Bor bzw. Aluminium für Si oder Ge) verunreinigt, sie also durch Diffusion oder Ionenimplantation als Fremdatome ins Kristallgitter einbaut (siehe Dotierung) ). Eine Leitung durch Defektelektronen kann aber auch durch Eigenleitung im undotierten Kristall entstehen, es entsteht durch Ionisation eines Gitter-Atomes ein Defektelektron und ein freies Elektron (das vormalige Valenzelektron). An diese freie Stelle in der Kristallstruktur kann nun ein benachbartes, freies Elektron hüpfen und das ersetzte Elektron wird z. B. durch Drift abgesaugt, was von außen betrachtet so interpretiert werden kann, als würde sich ein positiv geladenes Teilchen in entgegengesetzter Richtung bewegen (vergleichbar mit einer Luftblase in einer Flüssigkeit). Im Bändermodell spricht man dann von einem Übergang des Elektrons vom Valenz- ins Leitungsband (bzw. des Defektelektrons vom Leitungs- ins Valenzband), welcher beispielsweise durch thermische Anregung hervorgerufen werden kann.

Die interessante Physik des Halbleiters (Leitfähigkeit, optische Übergänge) spielt sich in einem Minimum des Leitungsbandes (Krümmung positiv = effektive Masse der Elektronen positiv) und in einem Maximum des Valenzbandes (Krümmung negativ = effektive Masse der Elektronen negativ) ab (während in einem Metall auch andere Konfigurationen vorkommen). Ein Elektron hat im Valenzband (in der Umgebung eines Maximums) eine negative effektive Masse (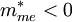$m_{me}^{*} < 0$) und bewegt sich somit bei äußerem elektrischen Feld zu niedrigeren elektrischen Potential, heißt zum Minus-Pol (im Gegensatz zu Elektronen im Leitungsband oder in Metallen). Geht ein Elektron (Ladung q_me − e) mit Impuls 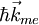$\hbar \vec{k}_{me}$ vom Valenzband in ein Akzeptorniveau oder in das Leitungsband über (thermische oder optische Anregung) dann bleibt im Valenzband ein unbesetzter Zustand zurück. Im vollbesetzten Band gibt es zu jedem positiven Impuls einen ebensogroßen negativen innerhalb der Fermifläche (im einfachsten Fall Fermikugel). Somit bleibt nach der Anregung im Valenzband ein unbesetzter Zustand und ein resultierender Impuls 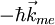$-\hbar\vec{k}_{me}$ zurück. Außerdem ist in dem vorher neutralen vollbesetzten Band durch Entfernen eines Elektrons eine resultierende positive Ladung + e zurückgeblieben. Dies lässt sich äquivalent als Loch beschreiben mit positiver Ladung + e, positiven Impuls 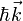$\hbar \vec{k}$ und positiver effektiver Masse 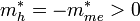$m_{h}^{*} = -m_{me}^{*} > 0$, somit ist die Bewegungsrichtung $\vec v$ gleich der des Elektrons im Valenzband das, also im äußeren elektrischen Feld zum Minus-Pol.

$q_{h}=-q_{me},\quad m_{h}^{*}=-m_{me}^{*},\quad\vec{k}_{h}=-\vec{k}_{me}$

Das entfernte Elektron (missing electron) hatte genau dieselbe Geschwindigkeit wie das nach der Anregung zurückgebliebene Loch (hole):

$\vec{v}_{me}=\hbar\frac{\vec{k}_{me}}{m_{me}^{*}}=\hbar\frac{\vec{k}_{h}}{m_{h}^{*}}=\vec{v}_{h}$

Ein äußeres elektrisches Feld beschleunigt das fehlende Elektron, wenn es im ursprünglichen Zustand sitzen würde, genauso wie das Loch:

$\frac{\mathrm{d}\vec{v}_{me}}{\mathrm{d}t}=\frac{q_{me}}{m_{me}^{*}}\vec{E}=\frac{q_{h}}{m_{h}^{*}}\vec{E}=\frac{\mathrm{d}\vec{v}_{h}}{\mathrm{d}t}$

Weitere wichtige charakteristische Größen von Halbleitern sind die Ladungsträgerbeweglichkeit und deren effektive Masse. Beide sind jedoch für Elektronen und Löcher nicht automatisch gleich groß und hängen beispielsweise auch von Material, Dotierung, Temperatur, Bewegungsrichtung usw. ab.

Beispiele aus der Anwendung

Die Erzeugung von Elektron-Loch-Paaren durch optische Anregung und anschließende Trennung derselben am p-n-Übergang wird in Solarzellen ausgenutzt, um Licht in elektrische Energie umzuwandeln.

Quellen

1. ↑ Rudolf Müller: Grundlagen der Halbleiter-Elektronik. 5. Auflage. Springer-Verlag, Berlin 1987. ISBN 3-540-18041-9, S. 25 und 30

Weblinks

• Alternative Erklärung des Defektelektrons im Techniklexikon.

Literatur

• Kopitzki, Herzog: Einführung in die Festkörperphysik. Teubner Verlag.
• Kittel: Einführung in die Festkörperphysik. Oldenbourg Verlag.
• Ashcroft, Mermin: Festkörperphysik. Oldenbourg Verlag