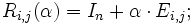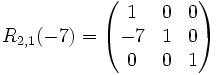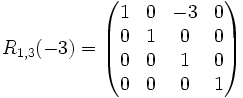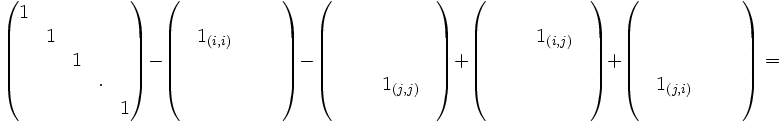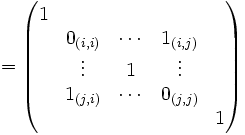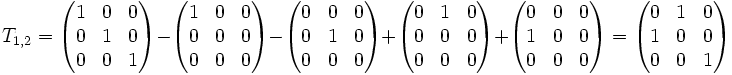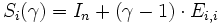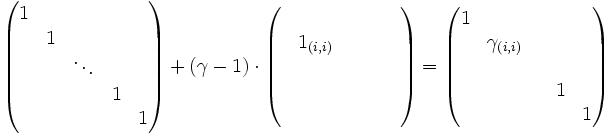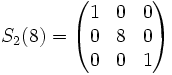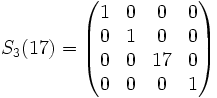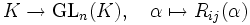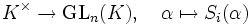- Elementare Zeilenumformung
-
Unter einer Elementarmatrix versteht man in der linearen Algebra eine quadratische Matrix, welche sich entweder durch die Änderung eines einzigen Eintrages oder durch Vertauschen zweier Zeilen von einer
 -Einheitsmatrix In unterscheidet. Multipliziert man eine
-Einheitsmatrix In unterscheidet. Multipliziert man eine 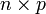 -Matrix A von links mit einer Elementarmatrix, so entspricht das elementaren Zeilenumformungen der Matrix A. Diese umfassen das Addieren des α-fachen einer Zeile zu einer anderen, das Vertauschen von zwei Zeilen und das Multiplizieren einer einzelnen Zeile mit einem von Null verschiedenen Wert γ. Die Elementarmatrizen sind die Grundlage für den Gauß-Algorithmus. Mit ihnen kann ein lineares Gleichungssystem, welches in eine Matrix überführt wurde, auf Stufenform gebracht werden, um dann die Lösung des Systems nach speziellen Regeln abzulesen.
-Matrix A von links mit einer Elementarmatrix, so entspricht das elementaren Zeilenumformungen der Matrix A. Diese umfassen das Addieren des α-fachen einer Zeile zu einer anderen, das Vertauschen von zwei Zeilen und das Multiplizieren einer einzelnen Zeile mit einem von Null verschiedenen Wert γ. Die Elementarmatrizen sind die Grundlage für den Gauß-Algorithmus. Mit ihnen kann ein lineares Gleichungssystem, welches in eine Matrix überführt wurde, auf Stufenform gebracht werden, um dann die Lösung des Systems nach speziellen Regeln abzulesen.Inhaltsverzeichnis
Typen von Elementarmatrizen
Man unterscheidet drei Typen von Elementarmatrizen:
(hier sei K ein Körper, In eine
 Einheitsmatrix und Ei,j eine
Einheitsmatrix und Ei,j eine  Standardmatrix (d.h. eine Matrix aus Nullelementen, mit der Ausnahme, dass an der Stelle i,j ein Einselement steht), wobei i als Zeilenindex und j als Spaltenindex der Matrizen verwendet wird)
Standardmatrix (d.h. eine Matrix aus Nullelementen, mit der Ausnahme, dass an der Stelle i,j ein Einselement steht), wobei i als Zeilenindex und j als Spaltenindex der Matrizen verwendet wird)Typ 1
Diese Matrix hat in ihrer Hauptdiagonale nur Einselemente, ansonsten nur Nullelemente, mit der Ausnahme der Stelle i,j, wo der Wert
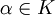 steht, wobei
steht, wobei 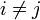 sein muss (d.h. der Wert α darf nicht in der Hauptdiagonalen stehen - sehr wohl aber in einer Zeile und Spalte ober- oder unterhalb dieser).
sein muss (d.h. der Wert α darf nicht in der Hauptdiagonalen stehen - sehr wohl aber in einer Zeile und Spalte ober- oder unterhalb dieser).Erzeugt wird dies durch
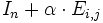 , wobei
, wobei 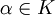 und
und 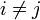 ist
ist
Zur Abkürzung schreiben wir
man beachte jedoch, dass es sich dabei nicht um eine Standardnotation handelt.
Ri,j(α) führt damit folgende Operationen aus:
Diese Elementarmatrix fügt also das Element α an der Stelle ij der Einheitsmatrix In ein.
Beispiele
Typ 2
Diese Matrix entspricht einer Einheitsmatrix In, in der die i-te mit der j-ten Zeile vertauscht wurde. Dabei wird in der Hauptdiagonale von In an den Stellen i,i und j,j das Einselement weggezählt (um Null zu erhalten) und an den Stellen i,j und j,i das Einselement wieder hinzugefügt. Außerdem gilt wieder, dass
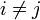 sein muss.
sein muss.Folgende Matrizenoperationen führen dies aus:
- In − Ei,i − Ej,j + Ei,j + Ej,i ,für
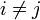
Zur Abkürzung definieren wir hier den Typ 2 als
- Ti,j = In − Ei,i − Ej,j + Ei,j + Ej,i
Die Operationen sehen allgemein so aus:
Das folgende Beispiel zeigt, wie die i-te mit der j-ten Zeile vertauscht wird:Beispiel
Typ 3
Die Hauptdiagonale dieser Matrix besteht aus Einselementen, bis auf die Stelle i,i wo der Wert
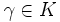 eingefügt wird, der ungleich Null sein muss. Außerhalb der Hauptdiagonale stehen nur Nullelemente.
eingefügt wird, der ungleich Null sein muss. Außerhalb der Hauptdiagonale stehen nur Nullelemente.Dies wird erreicht über
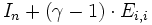 , mit
, mit 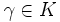 und
und 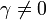
(An der Stelle i,i wird γ hinzugezählt und 1 abgezogen.)
Zur Abkürzung soll hier der Typ 3 als
definiert werden. Wiederum handelt es sich nicht um eine Standardnotation.
Ausgeführte Operationen:
Diese Elementarmatrix fügt in die Hauptdiagonale der neutralen Matrix In das Element γ ein.
Beispiele
Einfluss der Elementarmatrizen auf andere Matrizen
Sei A eine
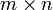 -Matrix und Ri,j(α), Ti,j und Si(γ) jeweils Matrizen vom Typ 1, Typ 2 und Typ 3.
-Matrix und Ri,j(α), Ti,j und Si(γ) jeweils Matrizen vom Typ 1, Typ 2 und Typ 3.Multiplikation von links ergibt Zeilenumformungen:
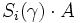 multipliziert die i-te Zeile von A mit dem Wert γ, wobei die übrigen Zeilen unverändert bleiben (EZU I)
multipliziert die i-te Zeile von A mit dem Wert γ, wobei die übrigen Zeilen unverändert bleiben (EZU I)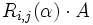 addiert das α-fache der j-ten Zeile von A zur i-ten Zeile von A. (EZU II)
addiert das α-fache der j-ten Zeile von A zur i-ten Zeile von A. (EZU II)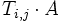 vertauscht die i-te Zeile von A mit der j-ten Zeile von A. (EZU III)
vertauscht die i-te Zeile von A mit der j-ten Zeile von A. (EZU III)
Multiplikation von rechts ergibt Spaltenumformungen:
 multipliziert die i-te Spalte von A mit dem Wert γ, wobei die übrigen Spalten unverändert bleiben. (ESU I)
multipliziert die i-te Spalte von A mit dem Wert γ, wobei die übrigen Spalten unverändert bleiben. (ESU I)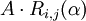 addiert das α-fache der i-ten Spalte von A zur j-ten Spalte von A. (ESU II) Man beachte die vertauschte Bedeutung von i und j im Gegensatz zur Zeilenumformung.
addiert das α-fache der i-ten Spalte von A zur j-ten Spalte von A. (ESU II) Man beachte die vertauschte Bedeutung von i und j im Gegensatz zur Zeilenumformung.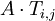 vertauscht die i-te Spalte von A mit der j-ten Spalte von A. (ESU III)
vertauscht die i-te Spalte von A mit der j-ten Spalte von A. (ESU III)
Siehe hierzu auch Matrizenmultiplikation. Diese Eigenschaften sind wichtig für Lösungsverfahren von Matrizenrechnungen, wie zum Beispiel dem Gauß-Jordan-Algorithmus.
Merkhilfe: Um für eine der oben genannten Umformungen die passende Elementarmatrix zu konstruieren, muss die entsprechende Umformung auf die Einheitsmatrix In angewendet werden. Um beispielsweise die Elementarmatrix zu erhalten, die die erste und zweite Zeile einer Matrix vertauscht, werden die erste und zweite Zeile der Einheitsmatrix vertauscht, wodurch sich T1,2 ergibt.
Generelle Eigenschaften
- Elementare Zeilenumformungen (bzw. Spaltenumformungen) ergeben sich durch Linksmultiplikation (bzw. Rechtsmultiplikation) mit einer Elementarmatrix.
- Der Rang einer Matrix ändert sich durch elementare Zeilen- oder Spaltenumformungen nicht.
- Ist ein lineares Gleichungssystem in der Form (A,b) mit
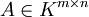 und
und 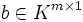 gegeben, dann ändern folgende Operationen (ermöglicht durch Multiplikation mit Elementarmatrizen) nichts an der Lösung und werden deshalb auch elementare Umformungen genannt (wobei die Operationen auf A und b gleichzeitig auszuführen sind):
gegeben, dann ändern folgende Operationen (ermöglicht durch Multiplikation mit Elementarmatrizen) nichts an der Lösung und werden deshalb auch elementare Umformungen genannt (wobei die Operationen auf A und b gleichzeitig auszuführen sind):
- Das Addieren des α-fachen Wertes einer Zeile zu einer anderen Zeile.
- Das Vertauschen zweier Zeilen.
- Das Multiplizieren einer Zeile mit einem Wert ungleich Null.
Gruppentheoretische Eigenschaften
Es sei GLn(K) die Gruppe der invertierbaren n×n-Matrizen.
- Elementarmatritzen sind invertierbar, und die Zuordnungen
-
- sowie
- sind Gruppenhomomorphismen. Insbesondere gilt
- Rij(α) − 1 = Rij( − α)
- und
- Si(α) − 1 = Si(α − 1).
- Die Matrizen Tij sind ihre eigenen Inversen:
- Jede invertierbare Matrix lässt sich als Produkt von Elementarmatrizen schreiben, d.h. die Elementarmatrizen erzeugen die Gruppe GLn(K). Dafür genügen auch schon Typ 1 und Typ 3. Darauf beruht auch eine wichtige Anwendung von Elementarmatrizen: Um eine Aussage für alle invertierbaren Matrizen zu beweisen, genügen die folgenden zwei Punkte:
- Sie gilt für Elementarmatrizen.
- Gilt sie für Matrizen A und B, so gilt sie auch für ihr Produkt AB.
Wikimedia Foundation.