Entwicklungssatz von Shannon

Der Entwicklungssatz von Claude Shannon ist ein Satz über Boolesche Funktionen, der die Shannon-Zerlegung verwendet. Er lautet wie folgt:

y = f(x1,...,xi,...,xn)	=	$x_{i}f(x_1,...,x_{i-1},1,x_{i+1},...,x_n)\ \vee$
		$\overline {x_i}f(x_1,...,x_{i-1},0,x_{i+1},...,x_n)$

Diese Formel sieht zunächst etwas kompliziert aus. Die Aussage betrifft eine n-stellige Boolesche Funktion f und dabei insbesondere deren Parameter x_i. Man sagt auch, die Funktion f wird durch Anwendung des Satzes "nach x_i entwickelt". Wiederholt man die Anwendung des Satzes für eine beliebige Funktion f auf alle ihre n Parameter, so gelangt man zu einer Darstellung der Funktion, welche ausschließlich die Operatoren ∧, ∨ und ¬ verwendet.

Mit anderen Worten: Die rekursive Anwendung des Entwicklungssatzes von Shannon liefert einen Beweis, dass sich ausnahmslos jede Boolesche Funktion mittels der Operatoren ∧, ∨ und ¬ ausdrücken lässt. Darüber hinaus kann der Entwicklungssatz etwa zur Herleitung klammerfreier Ausdrücke verwendet werden.

Beispiel

Gegeben sei die Boolesche Funktion $y = f(x_{1},x_{2},x_{3}) = x_{1}x_{2}\overline {x_{3}} \vee \overline {x_{1}}x_{2} \vee \overline {x_{2}}x_{3}$.

Diese soll zunächst nach x₁, dann nach x₂ und schließlich nach x₃ entwickelt werden:

y	$= x_{1}[x_{2}\overline {x_{3}} \vee \overline {x_{2}}x_{3}] \vee \overline {x_{1}}[x_{2} \vee \overline {x_{2}}x_{3}]$ (Entwicklung nach x1)
	$= x_{1}[x_{2}(\overline {x_{3}}) \vee \overline {x_{2}}(x_{3})] \vee \overline {x_{1}}[x_{2}(1) \vee \overline {x_{2}}(x_{3})]$ (Entwicklung nach x2)
	$= x_{1}[x_{2}(\overline {x_{3}}) \vee \overline {x_{2}}(x_{3})] \vee \overline {x_{1}}[x_{2}(x_{3} \vee \overline {x_{3}}) \vee \overline {x_{2}}(x_{3})]$ (Entwicklung nach x3)
	$= x_{1}x_{2}\overline {x_{3}} \vee x_{1}\overline {x_{2}}x_{3} \vee \overline{x_{1}}x_{2}x_{3} \vee \overline {x_{1}}x_{2}\overline {x_{3}} \vee \overline {x_{1}}x_{3}\overline{x_{2}}\$ (Anwendung des Distributivgesetzes)

Als Diagramm

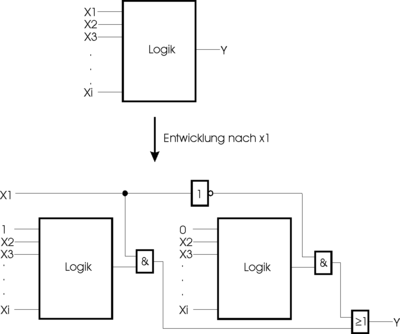
Man kann die Umformung auch als Multiplexer aus einem Nicht-Gatter, zwei UND sowie einem ODER-Gatter verstehen. Das Signal, nach dem die Zerlegung durchgeführt wird, ist das Steuersignal für den Multiplexer. Gemultiplext werden die beiden Ausgänge der gedoppelten Logik, wobei die eine Logik an dem entwickelten Eingang mit einer "1" beaufschlagt wird, während die andere mit einer "0" beaufschlagt wird. Als Diagram dargestellt, sieht dies forlgendermaßen aus:

Siehe auch

• Shannon-Zerlegung