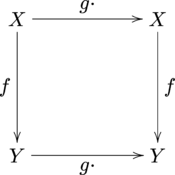
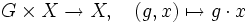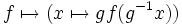equivariant — adjective Not affected by a specified group action. is equivariant with respect to : for every in , , where and are actions on different sets of the same group … Wiktionary
Equivariant map — In mathematics, an equivariant map is a function between two sets that commutes with the action of a group. Specifically, let G be a group and let X and Y be two associated G sets. A function f : X rarr; Y is said to be equivariant if: f ( g… … Wikipedia
Equivariant cohomology — In mathematics, equivariant cohomology is a theory from algebraic topology which applies to spaces with a group action . It can be viewed as a common generalization of group cohomology and an ordinary cohomology theory. Specifically, given a… … Wikipedia
Cartan connection — In the mathematical field of differential geometry, a Cartan connection is a flexible generalization of the notion of an affine connection. It may also be regarded as a specialization of the general concept of a principal connection, in which the … Wikipedia
Connection (principal bundle) — This article is about connections on principal bundles. See connection (mathematics) for other types of connections in mathematics. In mathematics, a connection is a device that defines a notion of parallel transport on the bundle; that is, a way … Wikipedia
Representation theory — This article is about the theory of representations of algebraic structures by linear transformations and matrices. For the more general notion of representations throughout mathematics, see representation (mathematics). Representation theory is… … Wikipedia
Michael Atiyah — Sir Michael Atiyah Born 22 April 1929 (1929 04 22) (age 82) … Wikipedia
Curtis–Hedlund–Lyndon theorem — The Curtis–Hedlund–Lyndon theorem is a mathematical characterization of cellular automata in terms of their symbolic dynamics. It is named after Morton L. Curtis, Gustav A. Hedlund, and Roger Lyndon; in his 1969 paper stating the theorem, Hedlund … Wikipedia
Affine connection — An affine connection on the sphere rolls the affine tangent plane from one point to another. As it does so, the point of contact traces out a curve in the plane: the development. In the branch of mathematics called differential geometry, an… … Wikipedia
Ehresmann connection — In differential geometry, an Ehresmann connection (after the French mathematician Charles Ehresmann who first formalized this concept) is a version of the notion of a connection which is defined on arbitrary fibre bundles. In particular, it may… … Wikipedia
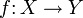 heißt G-äquivariant oder auch kurz äquivariant, wenn gilt:
heißt G-äquivariant oder auch kurz äquivariant, wenn gilt: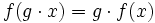 für alle
für alle 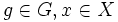 .
.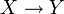 via
via