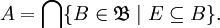Erzeugendensystem

Eine in der Mathematik häufig gebrauchte Methode ist die des Erzeugendensystems oder auch erzeugenden Systems. Dabei wird ein mathematisches Objekt mit Hilfe eines anderen, meist einfacheren Objekts beschrieben, so dass aus dem einfachen Objekt das Ursprungsobjekt konstruiert werden kann. Zum Beispiel heißt eine Menge 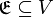$\mathfrak{E} \subseteq V$ von Vektoren eines K-Vektorraums V ein Erzeugendensystem eines Unterraums 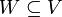$W \subseteq V$, falls jedes Element 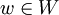$w \in W$ als Linearkombination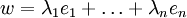

$w = \lambda_1 e_1 + \ldots + \lambda_n e_n$

durch Vektoren 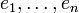$e_1,\ldots,e_n$ aus der Menge 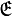$\mathfrak{E}$ darstellbar ist. Ist nun ein Vektorraum V gegeben, so kann man nach der kleinsten Anzahl von Vektoren fragen, welche V erzeugen. Dies führt auf den Begriff der Dimension eines Vektorraums. 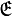Bei der komplementären Anwendung dieses Begriffes geht man von einer festen Menge $\mathfrak{E}$ von Vektoren aus, und fragt nach dem von $\mathfrak{E}$ erzeugten Unterraum. Dabei ist also ein Unterraum 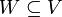$W \subseteq V$ gesucht, der 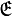$\mathfrak{E}$ enthält. Da der Durchschnitt einer nichtleeren Menge von Unterräumen wiederum Unterraum von V ist, und V einen Unterraum (sich selbst) besitzt der 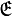$\mathfrak{E}$ enthält, kann man den Durchschnitt aller Unterräume von V betrachten, die 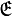$\mathfrak{E}$ enthalten. Dieser ist offenbar der kleinste Unterraum im Sinne der Inklusion, welcher die Eigenschaft besitzt 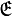$\mathfrak{E}$ als Teilmenge zu enthalten. Es ist nicht schwer, zu zeigen, dass dieser Unterraum genau der von 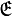$\mathfrak{E}$ im Sinne der vorherigen Definition erzeugte ist. Der Begriff des Erzeugendensystems tritt also in zwei Formen in Erscheinung: In der ersten Form geht man von einem mathematischen Objekt aus und versucht, dieses mittels eines Erzeugendensystems zu charakterisieren. In der zweiten Form möchte man ein mathematisches Objekt mit gewissen Eigenschaften, d. h. man geht von einem Erzeugendensystem aus. Dies ist jedoch nur dann sinnvoll, wenn vorher klar ist wo nach diesem Objekt gesucht werden soll. Im hier genannten Beispiel werden alle Unterräume eines Vektorraums betrachtet. Die zweite, implizite Formulierung dieses Prinzips hat den Vorteil für verschiedene Typen von mathematischen Objekten gleich zu sein. Diese Formulierung soll im Folgenden allgemein dargestellt werden.

Mengentheoretische Formulierung

Es sei eine Grundmenge X und ein System 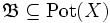$\mathfrak{B} \subseteq \operatorname{Pot}(X)$ von Teilmengen von X gegeben. Diese Teilmengen entsprechen dabei den mathematischen Objekten, die im Folgenden betrachtet werden. Im obigen Beispiel von Vektorräumen ist also X = V und 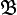$\mathfrak{B}$ die Menge der Unterräume von V. Sei weiter eine Menge 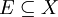$E \subseteq X$ gegeben. Dann wird nach der kleinsten Menge 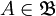$A \in \mathfrak{B}$ gefragt, so dass 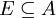$E \subseteq A$ gilt. Die Menge E ist also das Erzeugendensystem, im obigen Beispiel gilt also 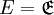$E = \mathfrak{E}$. Ein solches Element A existiert und ist eindeutig bestimmt, sofern gilt

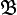1. $\mathfrak{B}$ ist stabil unter beliebigen Durchschnitten, d. h. ist 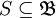$S \subseteq \mathfrak{B}$ nichtleere Teilmenge, so ist auch der Durchschnitt 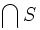$\bigcap S$ Element des Mengensystems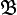 $\mathfrak{B}$
2. Es gibt mindestens ein Element A aus 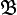$\mathfrak{B}$ mit der Eigenschaft 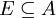$E \subseteq A$ (meist gilt $X\in\mathfrak B$).

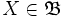Und zwar ist dann

$A = \bigcap \{ B \in \mathfrak{B} \mid E \subseteq B\}.$

Beispiele

Weitere Anwendungen des Prinzips des Erzeugendensystems:

• Auf Äquivalenzrelationen: Möchte man eine Äquivalenzrelation konstruieren, bei der gewisse Elemente gerade miteinander identifiziert werden, so hilft obige Konstruktion. Man benötigt solche Äquivalenzrelationen z. B. bei der Konstruktion von Quotientenräumen von Topologischen Räumen durch Verklebung.

Ist die gegebene Relation R, so kann man die erzeugte Äquivalenzrelation 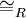$\cong_R$ auch dadurch beschreiben, dass 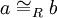$a\cong_Rb$ genau dann gilt, wenn

• a = b oder
• es gibt endlich viele Elemente 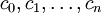$c_0, c_1, \ldots, c_n$ mit c₀ = a, c_n = b und für 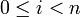$0\leq i<n$ jeweils c_iRc_{i + 1} oder c_{i + 1}Rc_i.

Die explizite Angabe ist hier also einigermaßen kompliziert.

• Auf Gruppen: Hier ist das betrachtete Mengensystem 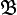$\mathfrak{B}$ die Menge der Untergruppen einer Gruppe G. Die von einer Teilmenge 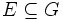$E \subseteq G$ erzeugte Untergruppe wird dabei üblicherweise mit 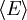$\langle E \rangle$ bezeichnet. Gilt 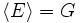$\langle E \rangle = G$, so sagt man, dass G von der Menge E erzeugt wird. Ist insbesondere E einelementig, d. h. 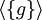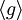E = {g}, so schreibt man statt $\langle\{g\}\rangle$ auch $\langle g \rangle$ und nennt 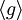$\langle g \rangle$ zyklisch. Für einelementige Erzeuger ist die erzeugte Untergruppe einfach die Menge 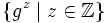$\{ g^z \mid z \in \mathbb{Z}\}$ der ganzzahligen Potenzen des Gruppenelementes.

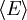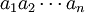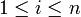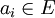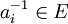Allgemein enthält $\langle E\rangle$ genau das neutrale Element von G sowie alle endlichen Produkte $a_1a_2\cdots a_n$ für die für $1\leq i\leq n$ jeweils $a_i\in E$ oder $a_i^{-1}\in E$ gilt.

• In der Maß- und Integrationstheorie untersucht man sogenannte σ-Algebren. Man betrachtet zum Beispiel einen topologischen Raum T und sucht in diesem eine σ-Algebra, die alle offenen Mengen enthält. In diesem Fall ist die Grundmenge X die Potenzmenge 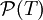$\mathcal{P}(T)$. Dem System 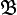$\mathfrak{B}$ entspricht die Menge der σ-Algebren auf T. Die dadurch eindeutig bestimmte σ-Algebra heißt die σ-Algebra der Borel-Mengen. Diese ist in der Integrationstheorie von zentraler Bedeutung. Hier steht die zweite Form des besagten Prinzips im Vordergrund, da das Objekt als solches nicht explizit angegeben werden kann.

Siehe auch

• Hüllenoperator