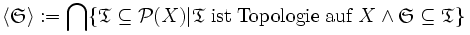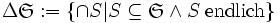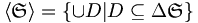- Erzeugnis (Raum)
-
Das Erzeugnis eines mathematischen Raumes, also einer Menge mit einer Struktur, beschreibt die strukturverträgliche Konstruktion einer Teilmenge dieses Raumes aus einer weiteren, erzeugenden Teilmenge des Raumes. Die erzeugende Menge wird manchmal Erzeugendensystem genannt. Die erzeugte Teilmenge nennt man das Erzeugnis der vorgegebenen Menge bzw. des Erzeugendensystems in dem betrachteten Raum.
Mit der Strukturverträglichkeit ist gemeint, dass die Axiome die für den Raum mit seiner Struktur gelten, auch für eine Teilmenge mit der entsprechend eingeschränkten Struktur gelten. Eine solche Teilmenge nennt man dann auch einen Unterraum.
Beispiele für Erzeugnisse sind
- die Menge der Linearkombinationen eines Erzeugendensystems in einem Vektorraum.
- das topologische Erzeugnis einer Teilmenge eines topologischen Raumes in diesem topologischen Raum.
- das Erzeugnis einer Teilmenge einer Gruppe in dieser Gruppe.
Der Artikel Hierarchie mathematischer Strukturen gibt einen guten Überblick über weitere Räume in denen eine Erzeugnisbildung betrachtet werden kann.
Inhaltsverzeichnis
Konstruktionsverfahren
Man betrachtet oft zwei unterschiedliche, bei sinnvoller Definition aber äquivalente, Konstruktionsverfahren, die so genannte Konstruktion von oben und von unten.
Bei der Konstruktion von oben betrachtet man den Schnitt aller Unterräume, welche das Erzeugendensystem umfassen. Da das Erzeugendensystem Teilmenge des betrachteten Raumes ist, ist stets der Raum selbst ein Unterraum, welcher das Erzeugendensystem umfasst. Das ist wichtig, damit die Definition sinnvoll ist, da der Schnitt über eine leere Menge selbst keine Menge ist.
Bei der Konstruktion von unten betrachtet man die Menge der möglichen Strukturkombinationen mit Elementen aus dem Erzeugendensystem. Beim Vektorraum etwa die Menge der Linearkombinationen mit Elementen des Erzeugendensystems.
Definitionen und Sätze
Das Erzeugendensystem eines Vektorraumes
Satz und Definition (Erzeugnis in einem Vektorraum)
Sei V ein Vektorraum über einem Körper K und
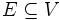 . Dann ist
. Dann istein Teilvektorraum von V und heißt das (Vektorraum-)Erzeugnis von E auf V.
Hinweise:
- Ist
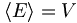 , so nennt man E ein Erzeugendensystem von V.
, so nennt man E ein Erzeugendensystem von V. - Ist E zusätzlich minimal, so nennt man E eine Basis von V.
Satz (Beschreibung "von unten")
Sei V ein Vektorraum über einem Körper K und
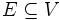 . Dann ist:
. Dann ist:Bedeutung in Worten
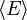 ist der kleinste K Vektorraum der E enthält.
ist der kleinste K Vektorraum der E enthält.Alle Elemente von
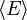 lassen sich als Linearkombination von Elementen aus E über K schreiben.
lassen sich als Linearkombination von Elementen aus E über K schreiben.Das topologische Erzeugnis
Satz und Definition (Das topologische Erzeugnis)
Sei X eine Menge und
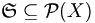 . Dann ist
. Dann isteine Topologie auf X und heißt das topologische Erzeugnis von
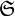 auf X.
auf X.Satz (Beschreibung "von unten")
Sei X eine Menge und
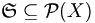 . Setze
. SetzeDann ist:
Bedeutung in Worten
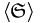 ist die kleinste (feinste) Topologie, so dass alle Elemente von
ist die kleinste (feinste) Topologie, so dass alle Elemente von 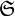 offen sind.
offen sind.Alle Elemente von
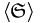 lassen sich als Vereinigung von endlichen Schnitten über
lassen sich als Vereinigung von endlichen Schnitten über 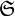 darstellen.
darstellen.Erzeugnis in einer Gruppe
Sei G eine Gruppe und M eine Teilmenge von G. Dann nennen wir den Durchschnitt aller Untergruppen von G, die M enthalten, das Erzeugnis von M und schreiben dafür
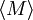 .
.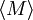 ist die kleinste Untergruppe von G, die M enthält.
ist die kleinste Untergruppe von G, die M enthält.
Wikimedia Foundation.

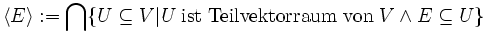
![\left\langle E \right\rangle = \{ \sum_{i=1}^{n}k_i v_i | n \in \mathbb{N} \wedge \forall i \in ( \mathbb{N} \cap [1,n] ): (k_i, v_i) \in K \times E \}](/pictures/dewiki/54/61633bfe6610064427d14c61356df82a.png)