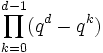- Hamelsche Basis
-
In der linearen Algebra ist eine Basis eine Teilmenge eines Vektorraumes, mit deren Hilfe sich jeder Vektor des Raumes eindeutig als endliche Linearkombination darstellen lässt. Die Koeffizienten dieser Linearkombination heißen die Koordinaten des Vektors bezüglich dieser Basis. Die Elemente der Basis heißen Basisvektoren. Wenn Verwechslungen zu befürchten sind, nennt man eine solche Teilmenge auch Hamelbasis (nach Georg Hamel). Ein Vektorraum besitzt im Allgemeinen verschiedene Basen und ein Wechsel der Basis erzwingt eine Koordinatentransformation.
Inhaltsverzeichnis
Definition und grundlegende Begriffe
Eine Basis eines Vektorraums V ist eine Teilmenge B von V mit folgenden gleichwertigen Eigenschaften:
- Jedes Element von V lässt sich als Linearkombination von Vektoren aus B darstellen und diese Darstellung ist eindeutig.
- B ist ein minimales Erzeugendensystem von V, jeder Vektor aus V lässt sich also als Linearkombination aus B darstellen (V ist Lineare Hülle von B) und diese Eigenschaft gilt nicht mehr, wenn ein Element aus B entfernt wird.
- B ist eine maximale linear unabhängige Teilmenge von V. Wird also ein weiteres Element aus V zu B hinzugefügt, ist die neue Menge nicht mehr linear unabhängig.
- B ist ein linear unabhängiges Erzeugendensystem von V.
Die Elemente einer Basis heißen Basisvektoren. Ist der Vektorraum ein Funktionenraum, nennt man die Basisvektoren auch Basisfunktionen. Eine Basis lässt sich mit Hilfe einer Indexmenge I in der Form
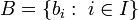 , eine endliche Basis beispielsweise in der Form
, eine endliche Basis beispielsweise in der Form 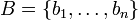 . Wird eine solche Indexmenge I benutzt, dann verwendet man jedoch meist zur Bezeichnung der Basis gleich die Familienschreibweise, d. h.
. Wird eine solche Indexmenge I benutzt, dann verwendet man jedoch meist zur Bezeichnung der Basis gleich die Familienschreibweise, d. h. 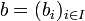 statt
statt 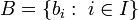 .
.Man beachte, dass sich in der Familienschreibweise eine Ordnung der Indexmenge I eine Anordnung der Basisvektoren erzeugt. Dies macht man sich bei der Beschreibung der Orientierung von Vektorräumen zu Nutze. Eine Indexmenge mit Ordnungsrelation ermöglicht es, unter den Basen Orientierungsklassen (Händigkeit) einzuführen. Beispiele: abzählbar unendliche Basis
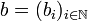 , endliche Basis
, endliche Basis 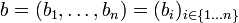 .
.Die Koeffizienten, die in der Darstellung eines Vektors als Linearkombination von Vektoren aus der Basis B auftreten, nennt man die Koordinaten des Vektors bezüglich B. Diese sind Elemente des dem Vektorraum zugrunde liegenden Körpers K (z. B.
 oder
oder  ). Zusammen bilden diese einen Koordinatenvektor
). Zusammen bilden diese einen Koordinatenvektor 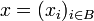 , der allerdings in einem anderen Vektorraum liegt, dem Koordinatenraum KB. Achtung: Da die Zuordnung der Koordinaten zu ihren jeweiligen Basisvektoren entscheidend ist, müssen hier - mangels einer gemeinsamen Indexmenge - die Basisvektoren selbst zur Indizierung herangezogen werden.
, der allerdings in einem anderen Vektorraum liegt, dem Koordinatenraum KB. Achtung: Da die Zuordnung der Koordinaten zu ihren jeweiligen Basisvektoren entscheidend ist, müssen hier - mangels einer gemeinsamen Indexmenge - die Basisvektoren selbst zur Indizierung herangezogen werden.Obwohl Basen meist als Mengen aufgeschrieben werden, ist daher eine durch eine Indexmenge I gegebene „Indizierung“ praktischer. Die Koordinatenvektoren haben dann die Form
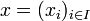 , der Koordinatenraum ist KI. Ist I geordnet, so defiert dies für den Koordinatenvektor eine Reihenfolge der Koordinaten. Im Beispiel
, der Koordinatenraum ist KI. Ist I geordnet, so defiert dies für den Koordinatenvektor eine Reihenfolge der Koordinaten. Im Beispiel 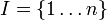 ist der Koordinatenvektor von der Form
ist der Koordinatenvektor von der Form 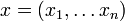 („Nummerierung“ der Koordinaten). Der Koordinatenraum ist hier Kn, bei reellen oder komplexen Vektorräumen also
(„Nummerierung“ der Koordinaten). Der Koordinatenraum ist hier Kn, bei reellen oder komplexen Vektorräumen also 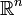 bzw.
bzw. 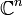 .
.Wichtige Eigenschaften
- Jeder Vektorraum hat mindestens eine Basis. Eine Beweisidee für diese Aussage ist im Abschnitt Existenzbeweis (Skizze) angegeben.
- Alle Basen eines Vektorraumes enthalten dieselbe Anzahl von Elementen. Diese Anzahl (die auch eine unendliche Kardinalzahl sein kann) nennt man die Dimension des Vektorraums.
- Eine Teilmenge
 eines K-Vektorraumes V definiert eine Abbildung
eines K-Vektorraumes V definiert eine Abbildung 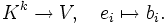
- Diese Abbildung ist genau dann
- Diese Charakterisierung überträgt sich auf den allgemeineren Fall von Moduln über Ringen, siehe Basis (Modul).
Beispiele
In der Euklidischen Ebene
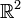 gibt es die so genannte kanonische Einheitsbasis {(1,0),(0,1)}. Darüber hinaus bilden in dieser Ebene zwei Vektoren genau dann eine Basis, wenn sie nicht dieselbe (oder entgegengesetzte) Richtung haben.
gibt es die so genannte kanonische Einheitsbasis {(1,0),(0,1)}. Darüber hinaus bilden in dieser Ebene zwei Vektoren genau dann eine Basis, wenn sie nicht dieselbe (oder entgegengesetzte) Richtung haben.Allgemeiner ist die kanonische Einheitsbasis des Vektorraums Kn die n-elementige Menge
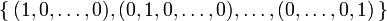 .
.Der einelementige Vektorraum {0} hat Dimension 0; seine (einzige) Basis ist die leere Menge.
Als
 -Vektorraum wird für
-Vektorraum wird für  meist die Basis {1,i} verwendet. Eine Menge
meist die Basis {1,i} verwendet. Eine Menge 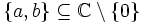 ist genau dann eine Basis von
ist genau dann eine Basis von  über
über  , wenn
, wenn 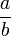 keine reelle Zahl ist. Als
keine reelle Zahl ist. Als  -Vektorraum hat
-Vektorraum hat  eine Basis, die man aber nicht explizit angeben kann.
eine Basis, die man aber nicht explizit angeben kann.Der Vektorraum der Polynome über einem Körper hat die Basis
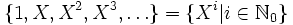 . Es gibt aber auch viele andere Basen, die zwar umständlicher anzuschreiben sind, aber in konkreten Anwendungen praktischer sind, z. B. die Legendre-Polynome.
. Es gibt aber auch viele andere Basen, die zwar umständlicher anzuschreiben sind, aber in konkreten Anwendungen praktischer sind, z. B. die Legendre-Polynome.Im Vektorraum der reellen Zahlenfolgen bilden die Vektoren
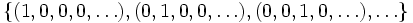 zwar ein linear unabhängiges System, aber keine Basis, denn es wird zum Beispiel die Folge
zwar ein linear unabhängiges System, aber keine Basis, denn es wird zum Beispiel die Folge 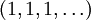 nicht davon erzeugt.
nicht davon erzeugt.Beweis der Äquivalenz der Definitionen
Die folgenden Überlegungen skizzieren einen Beweis dafür, dass die vier charakterisierenden Eigenschaften, die in diesem Artikel als Definition des Begriffs Basis genannt werden, äquivalent sind. (Für diesen Beweis wird das Auswahlaxiom oder Lemma von Zorn nicht benötigt.)
- Wenn sich jeder Vektor eindeutig als Linearkombination von Vektoren in B darstellen lässt, dann ist B insbesondere ein Erzeugendensystem (nach Definition).
Wenn B nicht minimales Erzeugendensystem ist, dann gibt es eine echte Teilmenge B', die auch ein Erzeugendensystem ist. Sei nun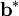 ein Element von B, welches nicht in B' liegt. Dann lässt sich
ein Element von B, welches nicht in B' liegt. Dann lässt sich 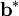 auf mindestens zwei verschiedene Arten als Linearkombination von Vektoren in B darstellen. Nämlich einmal als Linearkombination von Vektoren in B' und einmal als
auf mindestens zwei verschiedene Arten als Linearkombination von Vektoren in B darstellen. Nämlich einmal als Linearkombination von Vektoren in B' und einmal als 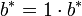 . Es ergibt sich ein Widerspruch und daher ist B minimal.
. Es ergibt sich ein Widerspruch und daher ist B minimal.
Also gilt (1) → (2).
- Jedes minimale Erzeugendensystem muss linear unabhängig sein. Denn wenn B nicht linear unabhängig ist, dann gibt es einen Vektor b * in B, welcher sich als Linearkombination von Vektoren in
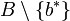 darstellen lässt. Dann aber lässt sich jede Linearkombination von Vektoren in B auch durch eine Linearkombination von Vektoren in
darstellen lässt. Dann aber lässt sich jede Linearkombination von Vektoren in B auch durch eine Linearkombination von Vektoren in 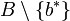 umschreiben und B wäre nicht minimal.
umschreiben und B wäre nicht minimal.
Also gilt (2) → (4).
- Jedes linear unabhängige Erzeugendensystem B muss eine maximale linear unabhängige Menge sein. Wäre nämlich B nicht maximal linear unabhängig, so gäbe es ein b * (das nicht in B liegt), welches zusammen mit B linear unabhängig wäre. Aber b * lässt sich als Linearkombination von Elementen von B darstellen, was der linearen Unabhängigkeit widerspricht.
Also gilt (4) → (3).
- Ein maximal linear unabhängiges System B ist ein Erzeugendensystem: Sei b * ein beliebiger Vektor. Wenn b * in B enthalten ist, dann lässt sich b * als Linearkombination von Elementen von B schreiben. Wenn aber b * nicht in B enthalten ist, dann ist die Menge
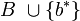 eine echte Obermenge von B und damit nicht mehr linear unabhängig. Die Vektoren
eine echte Obermenge von B und damit nicht mehr linear unabhängig. Die Vektoren 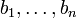 , die in einer möglichen lineare Abhängigkeit
, die in einer möglichen lineare Abhängigkeit  vorkommen, können nicht alle aus B sein, daher muss einer davon (sagen wir b1) gleich b * sein, mit a1 ungleich 0. Daher ist
vorkommen, können nicht alle aus B sein, daher muss einer davon (sagen wir b1) gleich b * sein, mit a1 ungleich 0. Daher ist 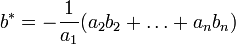 .
.
Also gilt (3) → (1).
Existenzbeweis (Skizze)
Mit dem Lemma von Zorn kann man beweisen, dass jeder Vektorraum eine Basis haben muss, auch wenn man sie oft nicht explizit angeben kann. (Umgekehrt kann man aus dem Satz, dass jeder Vektorraum eine Basis hat, auch das Auswahlaxiom oder das Lemma von Zorn beweisen. Daher kann man in einer Mengenlehre ohne das Auswahlaxiom oder äquivalente Aussagen nicht beweisen, dass jeder Vektorraum eine Basis hat.)
Sei V ein Vektorraum. Man möchte eine maximale linear unabhängige Teilmenge des Vektorraums finden. Es liegt also nahe, das Mengensystem
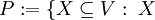 linear unabhängig }
linear unabhängig }
zu betrachten, das durch die Relation
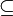 halbgeordnet wird. Man kann nun zeigen:
halbgeordnet wird. Man kann nun zeigen:- P ist nicht leer (zum Beispiel enthält P die leere Menge). Besteht V nicht nur aus dem Nullvektor, dann ist zusätzlich auch jede Einermenge
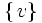 mit
mit 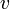 in
in 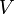 und
und 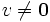 ein Element von P.
ein Element von P. - Für jede Kette
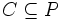 ist auch
ist auch 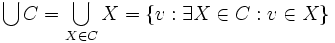 in P.
in P.
Aus dem Lemma von Zorn folgt nun, dass P ein maximales Element hat. Es folgt sogar, dass jedes Element T von P in einem maximalen Element von P enthalten ist. Die maximalen Elemente von P sind nun aber genau die maximalen linear unabhängigen Teilmengen von V, also die Basen von V. Daher hat V eine Basis und es gilt darüber hinaus, dass jede linear unabhängige Teilmenge von V in einer Basis von V enthalten ist.
Weitere Aussagen über Basen
- Austauschlemma von Steinitz (nach E. Steinitz): Sind
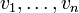 eine Basis eines Vektorraumes V und w ein weiterer vom Nullvektor verschiedener Vektor aus V, so kann man einen der Basisvektoren gegen w „austauschen“, d. h. es existiert ein Index
eine Basis eines Vektorraumes V und w ein weiterer vom Nullvektor verschiedener Vektor aus V, so kann man einen der Basisvektoren gegen w „austauschen“, d. h. es existiert ein Index 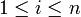 , sodass
, sodass 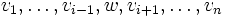 ebenfalls eine Basis von V ist.
ebenfalls eine Basis von V ist.
Diese Aussage wird häufig dazu benutzt, um zu zeigen, dass alle Basen eines Vektorraumes aus der gleichen Anzahl an Vektoren bestehen. - Jeder Vektorraum ist ein freies Objekt über seiner Basis. Dies ist eine universelle Eigenschaft von Vektorräumen im Sinne der Kategorientheorie. Konkret heißt dies:
-
- Eine lineare Abbildung eines Vektorraums in einen anderen Vektorraum ist bereits durch die Bilder der Basisvektoren vollständig bestimmt.
- Jede beliebige Abbildung der Basis in den Bildraum definiert eine lineare Abbildung.
- In einem d-dimensionalen Vektorraum über einem endlichen Körper mit q Elementen gibt es
-
- verschiedene Basen.
Basisbegriffe in speziellen Vektorräumen
Reelle und komplexe Vektorräume tragen meist zusätzliche topologische Struktur. Aus dieser Struktur kann sich ein Basisbegriff ergeben, der vom hier beschriebenen abweicht.
Abweichender Basisbegriff in Innenprodukträumen
Beim Studium von reellen oder komplexen Innenprodukträumen, besonders von Hilberträumen gibt es noch eine andere, dort zweckmäßigere Art, die Elemente des Raumes darzustellen. Eine Basis besteht dabei aus paarweise orthogonalen Einheitsvektoren, und es werden nicht nur endliche, sondern auch unendliche Summen (sog. Reihen) von Basisvektoren zugelassen. Ein solches vollständiges Orthonormalsystem ist in einem unendlichdimensionalen Raum im allgemeinen keine Basis im hier definierten Sinne, zur besseren Unterscheidung spricht man auch von Schauderbasis. Der im vorliegenden Artikel beschriebene Basis-Typ wird zur Unterscheidung auch Hamelbasis genannt.
Abgrenzung der Basisbegriffe
- Sowohl eine Hamelbasis als auch eine Schauderbasis ist eine linear unabhängige Menge von Vektoren.
- Eine Hamelbasis oder einfach Basis, wie sie in diesem Artikel beschrieben ist, bildet ein Erzeugendensystem des Vektorraums, d. h. ein beliebiger Vektor des Raums lässt sich als Linearkombination aus endlich vielen Vektoren der Hamelbasis darstellen.
- Bei einem endlichdimensionalen reellen oder komplexen Innenproduktraum ist eine Orthonormalbasis (d. h. ein minimales Erzeugendensystem aus normierten, zueinander senkrechten Vektoren) zugleich Hamel- und Schauderbasis.
- Bei einem unendlichdimensionalen, vollständigen reellen oder komplexen Innenproduktraum (speziell also in einem unendlichdimensionalen Hilbertraum) ist eine Schauderbasis nie eine Hamelbasis und umgekehrt. Im unendlichdimensionalen Fall lässt sich eine Hamelbasis häufig nicht einmal orthonormieren.
- Die Hamelbasis eines unendlichdimensionalen, separablen Hilbertraumes besteht aus überabzählbar vielen Elementen. Eine Schauderbasis hingegen besteht in diesem Fall aus abzählbar vielen Elementen.
- In Hilberträumen ist mit Basis (ohne Zusatz) meistens eine Schauderbasis gemeint, in Vektorräumen ohne Innenprodukt immer eine Hamelbasis.
Auerbachbasen
Eine Auerbachbasis ist eine Hamelbasis für einen dichten Unterraum in einem normierten Vektorraum, sodass der Abstand jedes Basisvektors vom Erzeugnis der übrigen Vektoren gleich seiner Norm ist.
Siehe auch
Literatur
- Uwe Storch, Hartmut Wiebe: Lehrbuch der Mathematik, Band II: Lineare Algebra. BI-Wissenschafts-Verlag, 1990, ISBN 3-411-14101-8
Wikimedia Foundation.