Euklids Beweis der Irrationalität der Wurzel aus 2

Euklid von Alexandria

Euklid überlieferte einen Beweis dafür, dass die Quadratwurzel von 2 irrational ist. Dies gilt als eine der wichtigsten Aussagen der Mathematik, teilweise wird sie sogar als der wichtigste mathematische Satz überhaupt angesehen, so beispielsweise auf der 1999 von den Mathematikern Paul und Jack Abad präsentierten Liste der 100 wichtigsten mathematischen Sätze.^[1]

Der unten angeführte Beweis stammt von Euklid aus Buch X der Elemente. Irrationale Größenverhältnisse waren aber schon dem Pythagoreer Archytas bekannt, der Euklids Satz nachweislich schon in allgemeinerer Form bewies. Das Weltbild der Pythagoreer, die die (natürliche) Zahl als das Maß aller Dinge betrachteten, war durch die Entdeckung der Irrationalität in Frage gestellt.

Ein geometrischer Beweis dafür, dass Diagonale und Seite im Quadrat oder im regelmäßigen Fünfeck keine gemeinsame Maß-Teilstrecke haben können, war bereits etwa 100 Jahre vorher von Hippasos von Metapont entdeckt worden.

Der zahlentheoretische Beweis Euklids wird indirekt durch Widerspruch geführt.

Beweisführung

Behauptung

Die Quadratwurzel von 2 ist eine irrationale Zahl.

Beweis

Die Beweisführung ist indirekt, d. h., es wird gezeigt, dass die Annahme des Gegenteils zu einem Widerspruch führt (lateinisch: reductio ad absurdum).

Wir nehmen also an, dass die Quadratwurzel von 2 rational ist. Es existieren also zwei teilerfremde ganze Zahlen p und q, so dass

$\sqrt[2\,]{2} = R = \frac{p}{q}$

und der Bruch nicht gekürzt werden kann.

Das heißt, es gibt einen Bruch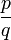 $\frac{p}{q}$, dessen Quadrat 2 ist.

$\left( \frac{p}{q} \right)^2 = 2$,

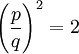umgeformt

p² = 2q².

Da die rechte Seite der Gleichung gerade ist, ist auch die linke Seite p² gerade. Daraus folgt, dass bereits die Zahl p gerade ist.

Wir bezeichnen die ganze Zahl 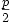$\tfrac{p}{2}$ als r und erhalten

2q² = p² = (2r)² = 4r²

und hieraus nach der Division durch 2

q² = 2r².

Mit der gleichen Argumentation wie zuvor folgt, dass q² und damit auch q gerade Zahlen sind.

Der Bruch kann also durch 2 gekürzt werden, 2 ist ein gemeinsamer Teiler von p und q. Dies aber ist ein Widerspruch zu unserer Voraussetzung, dass p und q teilerfremd sind.

Die Annahme, die Behauptung wäre falsch, führt also zu einem Widerspruch. Damit ist die Behauptung richtig und der Beweis ist abgeschlossen.

Verallgemeinerung

Die Beweisidee Euklids lässt sich auf den allgemeinen Fall der k-ten Wurzel aus einer beliebigen natürlichen Zahl n, die keine k-te Potenz ist, erweitern:

Wenn n keine k-te Potenz ist (nicht darstellbar als n = z^k für eine natürliche Zahl z), dann ist $\sqrt[k]{n}$ irrational.

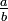Beweis: Anstelle der einfachen gerade-ungerade-Argumentation verwendet man hier allgemein die Existenz einer eindeutigen Primfaktorzerlegung für natürliche Zahlen. Der Beweis erfolgt wieder indirekt: Angenommen, es gelte $\sqrt[k]{n}=\tfrac ab$ mit natürlichen Zahlen a,b. Es ist zu zeigen, dass dann n eine k-te Potenz ist, d. h., dass $\tfrac ab$ sogar eine natürliche Zahl ist. Zunächst folgt durch einfache Umformung, dass 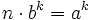$n\cdot b^k=a^k$ gilt. Sei p eine beliebige Primzahl. In der Primfaktorzerlegung von n bzw. a bzw. b trete p genau mit der Vielfachheit e_n bzw. e_a bzw. e_b auf. Dann folgt sofort 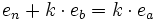$e_n + k\cdot e_b = k\cdot e_a$, wegen 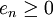$e_n\ge0$ auf jeden Fall also 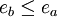$e_b \le e_a$. Da dies für jede Primzahl p gilt, muss b in der Tat ein Teiler von a sein, also ist 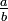$\tfrac ab$ eine natürliche Zahl und n ist deren k-te Potenz.

Einfache Folgerung aus dem Irrationalitätssatz:

$\sqrt[n]{n}$

ist irrational für alle natürlichen Zahlen > 1 (weil n nicht n-te Potenz einer natürlichen Zahl > 1 sein kann).

Einzelnachweise

1. ↑ The Hundred Greatest Theorems

Weblinks

• Hippasos geht Hops Beweis der Irrationalität von Wurzel 2 als Gedicht