- Wurzel 2
-
Unter Wurzel 2 (Quadratwurzel aus 2) versteht man in der Mathematik diejenige positive Zahl, deren Quadrat die Zahl 2 ergibt, also die Zahl x > 0, für die x2 = 2 gilt. Diese Zahl ist eindeutig bestimmt, irrational und wird durch
 dargestellt. Die ersten Stellen ihrer Dezimalbruchentwicklung sind:
dargestellt. Die ersten Stellen ihrer Dezimalbruchentwicklung sind:  = 1,414213562…
= 1,414213562…Inhaltsverzeichnis
Allgemeines
Irrationalität der Wurzel 2
Die Quadratwurzel aus 2 ist wie die Kreiszahl π oder die eulersche Zahl e irrational. Im Gegensatz zu den beiden ist sie jedoch nicht transzendent, sondern algebraisch. Bereits um 500 v. Chr. war dem Griechen Hippasos von Metapont die Irrationalität bekannt. Der bekannteste Beweis dafür stammt von dem im 4. Jahrhundert v. Chr. lebenden Griechen Euklid. Er gilt als der erste bekannte Widerspruchsbeweis in der Geschichte der Mathematik. Auch der Grieche Platon soll einen Beweis geliefert haben.
Nachkommastellen der Wurzel 2
Da Wurzel 2 irrational ist, hat die Zahl in jedem Stellenwertsystem unendlich viele nichtperiodische Nachkommastellen und lässt sich deshalb auch im Dezimalsystem nur näherungsweise darstellen. Die ersten 50 dezimalen Nachkommastellen lauten:
Kettenbruchentwicklung
Eine andere Möglichkeit, reelle Zahlen darzustellen, ist die Kettenbruchentwicklung. Die Kettenbruchdarstellung von Wurzel 2 ist – im Gegensatz zur Kreiszahl π – periodisch, denn Wurzel 2 ist eine quadratische Irrationalzahl. Für die n-te Wurzel aus 2 bei n > 2 trifft dies jedoch nicht zu.
Geometrische Konstruktion von Wurzel 2
Da irrationale Zahlen eine unendlich lange Dezimaldarstellung haben, ist es unmöglich, eine solche Zahl mit dem Lineal genau abzumessen. Es ist aber möglich, die Zahl
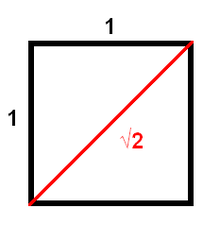
 mit Zirkel und Lineal zu konstruieren: Die Diagonale eines Quadrates ist
mit Zirkel und Lineal zu konstruieren: Die Diagonale eines Quadrates ist  -mal so lang wie seine Seitenlänge. Es reicht auch ein rechtwinkliges, gleichschenkliges Dreieck, bei dem die Katheten jeweils 1 Einheit lang sind. Die Länge der Hypotenuse beträgt dann
-mal so lang wie seine Seitenlänge. Es reicht auch ein rechtwinkliges, gleichschenkliges Dreieck, bei dem die Katheten jeweils 1 Einheit lang sind. Die Länge der Hypotenuse beträgt dann  Einheiten. Um dies zu beweisen, reicht der Satz des Pythagoras: Für die Länge x der Diagonale gilt x2 = 12 + 12.
Einheiten. Um dies zu beweisen, reicht der Satz des Pythagoras: Für die Länge x der Diagonale gilt x2 = 12 + 12.Das genannte Dreieck ist auch der Beginn der Quadratwurzelspirale.
Geschichte der Wurzel 2
Bereits die alten Hochkulturen haben sich Gedanken über die Wurzel aus 2 gemacht. Die alten Inder schätzen
 = 1,414215686… . Diese Näherung stimmt auf fünf Nachkommastellen mit dem tatsächlichen Wert von
= 1,414215686… . Diese Näherung stimmt auf fünf Nachkommastellen mit dem tatsächlichen Wert von  überein, die Abweichung beträgt nur +0,0001502 Prozent. Von ihrer Irrationalität wussten sie wahrscheinlich nichts. Die Babylonier wie auch die Sumerer schätzten um 1950 v. Chr. die Wurzel 2 umgerechnet noch auf 1,41. Aus der Zeit um 1800 v. Chr. ist von den Babyloniern eine weitere Näherung überliefert. Sie benutzten in ihrer Keilschrift ein Stellenwertsystem zur Basis 60 und berechneten die Näherung mit
überein, die Abweichung beträgt nur +0,0001502 Prozent. Von ihrer Irrationalität wussten sie wahrscheinlich nichts. Die Babylonier wie auch die Sumerer schätzten um 1950 v. Chr. die Wurzel 2 umgerechnet noch auf 1,41. Aus der Zeit um 1800 v. Chr. ist von den Babyloniern eine weitere Näherung überliefert. Sie benutzten in ihrer Keilschrift ein Stellenwertsystem zur Basis 60 und berechneten die Näherung mit = 1,414212962… [1]
= 1,414212962… [1]
Diese Näherung stimmt auf fünf Nachkommastellen mit dem tatsächlichen Wert von
 überein, die Abweichung beträgt nur −0,0000424 Prozent.
überein, die Abweichung beträgt nur −0,0000424 Prozent.Im späten 6. oder frühen 5. Jahrhundert v. Chr. entdeckte Hippasos von Metapont, ein Pythagoreer, entweder an einem Quadrat oder an einem regelmäßigen Fünfeck, dass das Verhältnis von Seitenlänge zu Diagonale nicht mit ganzen Zahlen darzustellen ist. Damit bewies er die Existenz inkommensurabler Größen. Eine antike Legende, wonach die Veröffentlichung dieser Erkenntnis von den Pythagoreern als Geheimnisverrat betrachtet wurde, ist nach heutigem Forschungsstand unglaubwürdig.
Sonstiges
- Shigeru Kondo veröffentlichte 2009 die ersten 200 Milliarden Nachkommastellen der Wurzel 2.[2] Der 2010 erzielte Rekord liegt bei 1 Billion Nachkommastellen (Stand: 23. März 2010).[3]
- Das Verhältnis der beiden Seitenlängen eines Blattes im DIN-A-Format beträgt
 mit Rundung auf ganze Millimeter und entgegen verbreiteter Annahme nicht den Goldenen Schnitt
mit Rundung auf ganze Millimeter und entgegen verbreiteter Annahme nicht den Goldenen Schnitt  . Dadurch ist sichergestellt, dass bei Halbierung des Blattes entlang der längeren Seite wieder ein Blatt im DIN-A-Format (mit um eins erhöhter Nummerierung) entsteht.
. Dadurch ist sichergestellt, dass bei Halbierung des Blattes entlang der längeren Seite wieder ein Blatt im DIN-A-Format (mit um eins erhöhter Nummerierung) entsteht. - Die Wurzel aus 2 ist das Frequenzverhältnis zweier Töne in der Musik bei gleichschwebender Stimmung, die einen Tritonus, also eine halbe Oktave bilden.
Merkhilfe für die ersten Nachkommastellen der Wurzel 2
Die ersten vier Zweierblöcke 14, 14, 21 und 35 der dezimalen Nachkommastellen von Wurzel 2 sind, aufgefasst als zweistellige Zahlen, alle durch sieben teilbar. Die vier darauffolgenden Ziffern lassen sich in die durch sieben teilbaren Blöcke 623 und 7 aufteilen.
Siehe auch
Einzelnachweise
- ↑ Kleiner Geschichtsabriss zur Computer-, Technik-, Kommunikations - und Mediengeschichte – Beitrag zum Schülerprojekt Meine Welt 2020. Reportagen aus der Zukunft, 31. März 2000
- ↑ Sqrt(2), Value of 200 billion digits below decimal point von Shigeru Kondo, 6. Mai 2009 (englisch)
- ↑ Constants and Records of Computation von Xavier Gourdon und Pascal Sebah, 23. März 2010 (englisch)
Weblinks
 Commons: Square root of 2 – Sammlung von Bildern, Videos und Audiodateien
Commons: Square root of 2 – Sammlung von Bildern, Videos und Audiodateien- Eric W. Weisstein: Pythagoras’s Constant. In: MathWorld. (englisch)
- Folge A028254 in OEIS (Engel-Entwicklung (engl. Engel expansion) von √2)
Wikimedia Foundation.


![\sqrt{2} = [1;\, 2,\, 2,\, 2,\, 2,\, 2,\, \ldots]](5/d5543d0bbfd63c021c2b00e8bdf945b5.png)