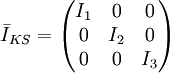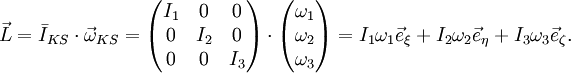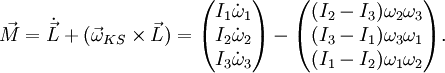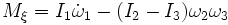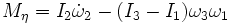Eulersche Kreiselgleichungen

Die eulerschen Gleichungen oder auch eulerschen Kreiselgleichungen sind Bewegungsgleichungen für die Rotation eines starren Körpers. Sie sind Differentialgleichungen im Hauptachsensystem mit der Winkelgeschwindigkeit 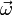$\vec\omega$ als Variable und den Hauptträgheitsmomenten I₁,I₂,I₃ als Koeffizienten.

Die eulerschen Gleichungen sind nicht zu verwechseln mit den eulerschen Winkeln, die die Orientierung eines körperfesten Koordinatensystems in bezug auf ein raumfestes Koordinatensystem beschreiben.

Herleitung

Die eulerschen Gleichungen folgen aus der Bewegungsgleichung des Drehimpulses, die gegeben ist durch

$\dot \vec L= \bar I \cdot \dot \vec\omega = \vec M$,

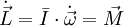wobei 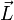$\vec L$ der Drehimpuls, 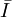$\bar I$ der Trägheitstensor und 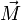$\vec M$ die Summe aller von außen auf den Körper wirkenden Drehmomente im Raumfesten Inertialsystem ist.

Durch Transformation ins Hauptachsensystem wird der im Inertialsystem im Allgemeinen zeitabhängige Trägheitstensor 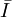$\bar I$ zeitunabhängig und nimmt die Form

$\bar I_{KS} = \begin{pmatrix} I_1 & 0 & 0 \\ 0 & I_2 & 0 \\ 0 & 0 & I_3 \end{pmatrix}$

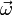an. $\vec \omega$ transformiert sich dabei zu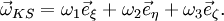 $\vec \omega_{KS} = \omega_1 \vec e_\xi + \omega_2 \vec e_\eta +\omega_3 \vec e_\zeta.$

Der Drehimpuls bekommt dadurch die sehr einfache Form

$\vec L=\bar I_{KS}\cdot\vec\omega_{KS}=\begin{pmatrix} I_1 & 0 & 0 \\ 0 & I_2 & 0 \\ 0 & 0 & I_3 \end{pmatrix} \cdot \begin{pmatrix}\omega_1 \\ \omega_2 \\ \omega_3 \end{pmatrix}=I_1 \omega_1 \vec e_\xi + I_2 \omega_2 \vec e_\eta +I_3 \omega_3\vec e_\zeta.$

Der Drehimpulssatz wird durch die Transformation des Bezugsystems zu

$\vec M=\dot \vec L + (\vec\omega_{KS} \times \vec L )= \begin{pmatrix}I_1 \dot\omega_1 \\ I_2 \dot \omega_2 \\ I_3 \dot\omega_3 \end{pmatrix}- \begin{pmatrix}(I_2 - I_3) \omega_2\omega_3 \\(I_3 - I_1) \omega_3\omega_1 \\(I_1 - I_2) \omega_1\omega_2 \end{pmatrix}.$

Hierbei ist, anders als in der ersten Zeile, 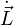$\dot \vec L$ als Zeitableitung des Drehimpulses im körperfesten Bezugssystem zu verstehen.

Komponentenweise ausformuliert bildet dies die eulerschen Gleichungen

$M_\xi=I_1 \dot\omega_1 -(I_2 - I_3) \omega_2\omega_3$

$M_\eta=I_2 \dot \omega_2-(I_3 - I_1) \omega_3\omega_1$

$M_\zeta=I_3 \dot\omega_3-(I_1 - I_2) \omega_1\omega_2$.

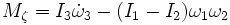Um diese Bewegungsgleichungen ausnutzen zu können, wird das äußere Drehmoment im körperfesten System benötigt.